三角幻方的研究
陜西省漢中市漢中中學 周小文
三角幻方的研究
陜西省漢中市漢中中學 周小文
三角幻方是從三階幻方當中脫衍出來的,大家耳熟能詳的九宮格就是三階幻方。三階幻方其實是正方形的,而三角幻方則不然,其本體是三角形的。最簡單的三角幻方是1~6構成的三角幻方,實質就是由1~6六個數字構成的等邊三角形。筆者主要研究的是1~9這九個數字構成的等邊三角形。
一、三角幻方的相關定義
三角幻方的定義與三階幻方的定義類似:將X個數字(X必須為3的倍數且最小為6)均勻填到三角形三邊中,使得三條邊上的數字之和剛好相等,我們就稱這個三角形為三角幻方。但是這里還有一個問題,同一組數字有兩種不同的填法,都能構成三角幻方,所以在命名三角幻方的時候,筆者總結出一種方式:X-Y-S-三角幻方。其中X是三角幻方的三個頂點,Y是三角幻方的幻和(三角幻方的幻和就是其邊長),S是三角幻方的階數。如圖1就叫作(1,5,9)-20-四階-三角幻方。

二、構造三角幻方的一般方法
先從最簡單的三角幻方談起。最簡單的三角幻方是由1~6構成的三角幻方。在開始之前,要介紹一下研究幻方的方法,或者說1~6的數字組合為什么能夠構成一個幻方。
筆者在研究三角幻方的時候用到了一種方法:先確定頂點數以及幻和,然后根據差值以及剩下的數來確定最后的三角幻方到底是哪一種。這種方法的根本是差值法。首先,我們如果確定了頂點的數字,那么這個三角幻方的幻和以及總和我們也就知道了,然后根據剩下的數字來最終確定這個三角幻方。但是,頂點上的數字也不是隨便填的,頂點上的數字之和必須是3的倍數(因為所有的數字加起來要是3的倍數,而1~6里面有三個數用了兩次,其余的數用了1次,所以1+2+3+4+5+6=21是3的倍數,剩下的三個數的和也必須是3的倍數),所以可以填的數字的組合只有1、2、3;1、2、6;1,3,5;1、5、6;2、3、4;2、4、6;3、4、5;4、5、6。
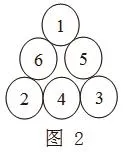
確定了頂點數,那么相對應的幻和也就確定了。以1、2、3為例,其幻和就是,那么1和2之間就差9-1-2=6,2和3之間就差9-2-3=4,1和3之間就差9-1-3=5。那么最后的三角幻方就是(1,2,3)-9-三階-三角幻方(如圖2所示)。
同樣的,用這樣的方法也就能夠確定剩下的幾組三角幻方是否存在了。經過驗證,以(1、3、5);(2、4、6);(4、5、6)為頂點的三角幻方都是存在的,而其他的都不存在,具體如圖3、圖4、圖5。
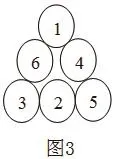
(1,3,5)-10-三階-三角幻方
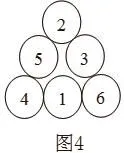
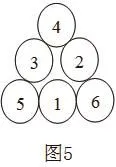
(2,4,6)-11-三階-三角幻方 (4,5,6)-12-三角幻方
1~6這六個數字所組成的三角幻方只有這些,并且也沒有太多的性質可以進行研究,所以接下來研究的是1~9這九個數字構成的三角幻方,如圖6。
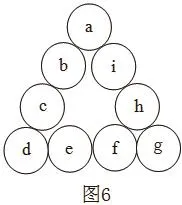
那么我們可以把 分成三個部分:A={1,4,7}(1~9中能被3除余1);B={2,5,8}(1~9中被3除余2);C={3,6,9}(1~9中能被3整除的數)。
那么我們就可以有三個取三角幻方頂點數的取法:
取法一: ,那么要么a,f,i都屬于A,要么a,f,i都屬于B;
取法二:a,d,g中只有一個屬于C,那么其余兩個數一個在A中取,一個在B中取;
共有30種取法,但30種取法里面又有多少種可以構成四階三角幻方呢?
(1,2,3)-17-四階-三角幻方、(1,4,7)-19-四階-三角幻方、(2,5,8)-20-四階-三角幻方、(2,3,7)-19-四階-三角幻方、(3,6,9)-21-四階-三角幻方、(4,5,6)-20-四階-三角幻方、(7,8,9)-23-四階-三角幻方是兩種填寫方式;而(1,5,9)-20-四階-三角幻方、(3,5,7)-20-四階-三角幻方只有一種填寫方式。

