高中數學中奇偶函數的圖象特征
◆段美伊
高中數學中奇偶函數的圖象特征
◆段美伊
周期性、奇偶性、連續性等都是函數學習當中學生應該掌握的知識點。其中,奇偶性是函數性質當中重要的組成部分,函數奇偶性是對函數概念以及相關知識點的深化和發展,對學生的理解能力以及邏輯思維能力提出了很高的要求。學生在學習函數奇偶性的過程中,應該重點掌握奇偶性的性質、定義、圖像的特征等,只有這樣才能做到有的放矢,進而實施有針對性的學習方法,提高學生的數學成績。本文主要對奇偶函數的特點進行了分析,并通過相關例題的解答,加深學生對對奇偶函數的理解,以此使高中學生全面掌握對奇偶函數相關知識點。
函數;奇偶性;定義域;圖像
一、奇偶函數定義的認識
(一)抽象化的認識。函數奇偶性是對函數概念以及相關知識點的深化和發展,對學生的理解能力以及邏輯思維能力提出了很高的要求。在函數單調性的基礎之上學習函數的奇偶性,學生能夠將相關的知識最大程度聯系起來,提高學習的效率。在函數奇偶性的學習當中,學生應該意識到函數奇偶性和函數的單調性一樣,不是客觀存在的,而是相關的數學教育工作者通過大量的函數關系式的研究,從結論當中抽象的概括出來的。同時對于函數奇偶性進行全面掌握,可以為后續關于函數知識的學習打下堅實的基礎,在對函數的奇偶性進行抽象學習以及思考的過程中,不僅要對函數奇偶性本身所具有的性質進行學習和掌握,同時還要對解題過程中涉及到的思維以及問題進行抽象化的思考。所以,學生在學習函數的時候,首先就要意識到函數具有較強的抽象性。
(二)形式化的認識。在對函數奇偶性進行定義的時候,數學符號不能直接反映文字的內涵和觀點,數學符號蘊含的是一種邏輯思維過程,在對函數奇偶性進行定義的時候,應該對其有一個抽象化的認識。比如f(x)、f(-x)、-f(x)都是對邏輯思維進行的一種本質的反映。這些數學符號,能夠直觀反映出函數關系式的特點以及性質。都有一個任意的點x在定義域內,對偶函數判斷的方法就是f(-x)=f(x),對奇函數的判斷方法就是f(-x)=-f(x)。
(三)數形結合的認識。在函數的學習過程當中,用來表達函數奇偶性的方式有很多種,不僅僅可以用文字語言對函數的關系式進行表達,同時還可以用符號,圖形來對函數的關系式進行描述。所以,學生在學習函數奇偶性的過程當中,不僅僅能夠解決函數奇偶性的判斷,畫出函數奇偶性的圖像。同時對于數形結合的函數題目也要運用相關的知識進行靈活處理,只有將數與形充分結合起來,才能全面掌握函數的規律以及解題的思路和技巧。
二、奇偶函數的圖像特征
在函數的關系式當中,對于奇偶性函數的圖像特征的描述是:奇函數的圖像是在坐標原點上對稱的,偶函數的圖像是關于坐標y軸對稱的。比如可以設f(x)為奇函數,同時還可以設f(x)的奇函數和f(x)的圖像是在原點對稱的,那么就會得出:(x,y)→(-x,-y)。因為在某一個區間上,偶函數是單調遞增的,所以它在對稱區間上則是單調遞減的,奇函數是單調遞增的,所以它在對稱區間上也是單調遞增的。在這里需要指出的是:(1)不管是奇、偶函數,它的定義域首先要對稱,定義域不對稱就沒有奇偶性可言,但是函數不一定是對稱的;(2)奇函數定滿足:f(-x)=-f(x),偶函數定滿足:f(-x)=f(x) ;(3)在圖像方面,若奇函數的定義域是R,那么就可以得出f(0)=0。
三、關于函數奇偶性的具體應用
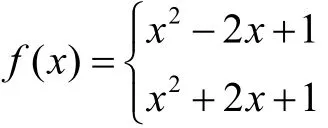
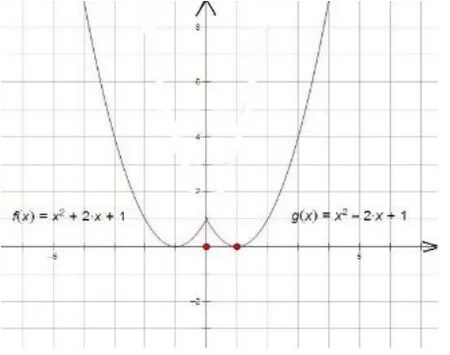
圖1
結束語
奇偶函數在高中數學中是一個非常重要的知識點,學生學習起來有一定難度,這種函數和圖像具有極其緊密的聯系。在學習的過程中,一定要加強對基礎概念、解題方法和圖像特征的研究學習,掌握更加全面的知識,提升自身奇偶函數的掌握水平。
[1]張海燕.高中函數解題教學的研究[D].湖南師范大學,2012.
(作者單位:湖南師范大學附屬中學)

