基于模型預測控制的智能汽車目標路徑跟蹤方法研究＊

段建民 田曉生 夏天 宋志雪

（北京工業大學，北京 100022）

基于模型預測控制的智能汽車目標路徑跟蹤方法研究＊

段建民 田曉生 夏天 宋志雪

（北京工業大學，北京 100022）

為避免智能汽車在目標路徑跟蹤過程中發生側滑，改善自動駕駛性能，通過改進目標函數、增加輪胎側偏角動力學約束，以車輛動力學模型作為模型預測控制的預測模型，提出了一種改進的智能汽車目標路徑跟蹤方法。在CarSim與MATLAB/Simulink聯合仿真平臺對該方法進行了驗證，結果表明，該方法有效地降低了智能汽車跟蹤目標路徑時發生側滑的幾率，提高了智能汽車目標路徑跟蹤的準確性和安全性。

1 前言

路徑跟蹤指無人駕駛車輛沿著設定的路徑安全、穩定、準確地行駛，其性能直接影響智能車自主行駛的能力[1]。早期的路徑跟蹤控制方法（如純跟蹤算法Pure pursuit[2]、環形預瞄法Circular Look-Ahead[3]等）使用幾何方法進行路徑跟蹤，但不同于以往的四輪機器人，車輛由于尺寸較大，受最小轉彎半徑、最大角速度等動力學條件的約束[4]，傳統的基于幾何的路徑跟蹤方法并不能很好地解決車輛的這些約束問題。

基于模型預測控制的路徑跟蹤控制算法已在國內外得到了廣泛應用，文獻[4]依據被控對象的運動學模型，對系統狀態量的偏差和控制量進行優化，該方法雖簡單實用，但無法對每個采樣周期內的控制增量進行限制，無法避免被控系統狀態量發生突變。文獻[5]對該系統的空間方程進行了轉換，實現了對控制增量的約束，但仍采用車輛運動學模型，不能對車輛動力學指標進行約束，無法滿足車輛的安全行駛要求。文獻[6]提出了基于線性時變動力學模型預測控制的路徑跟蹤算法，但并未考慮到車輛在高速行駛時的穩定性問題，只對狀態量進行約束，沒有對車輛進行動力學約束。

本文針對以上路徑跟蹤研究中存在的問題，以車輛動力學模型作為預測模型，充分發揮模型預測控制解決多約束問題的優點，通過改進優化目標函數減少優化目標的數量來提高控制算法的實時性，通過加入車輪側偏角的動力學約束來提高智能車跟蹤目標路徑時的平穩性和安全性。

2 車輛動力學模型及其線性化

2.1 車輛動力學模型

本文用車輛四輪模型來分析車輛在運動過程中的受力情況[7]，為簡化計算，假設車輛在水平路面上行駛，不考慮橫向和縱向空氣阻力。滿足以上條件的車輛動力學模型如圖1所示，其中，oxy為車體坐標系，規定x軸正向為車頭方向，y軸為車體橫向，OXY為大地坐標系。

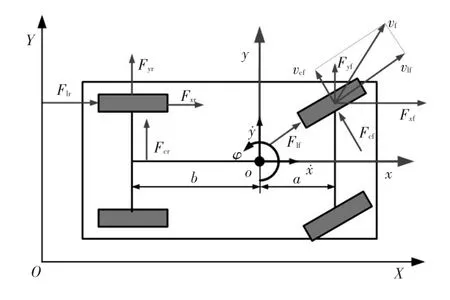
圖1 車輛動力學模型

根據牛頓第二定律，分別得到沿x軸、y軸和繞z軸的受力平衡方程：

式中，a、b分別為質心到前、后軸的距離；m為車輛的質量；Iz為車輛繞z軸的轉動慣量；φ為車輛航向角；Fxf、Fxr為車輛前、后車輪受到的x方向的力；Fyf、Fyr為車輛前、后車輪受到的y方向的力。

經過簡化整理，可以得到較小前輪偏角假設下的車輛動力學非線性模型：

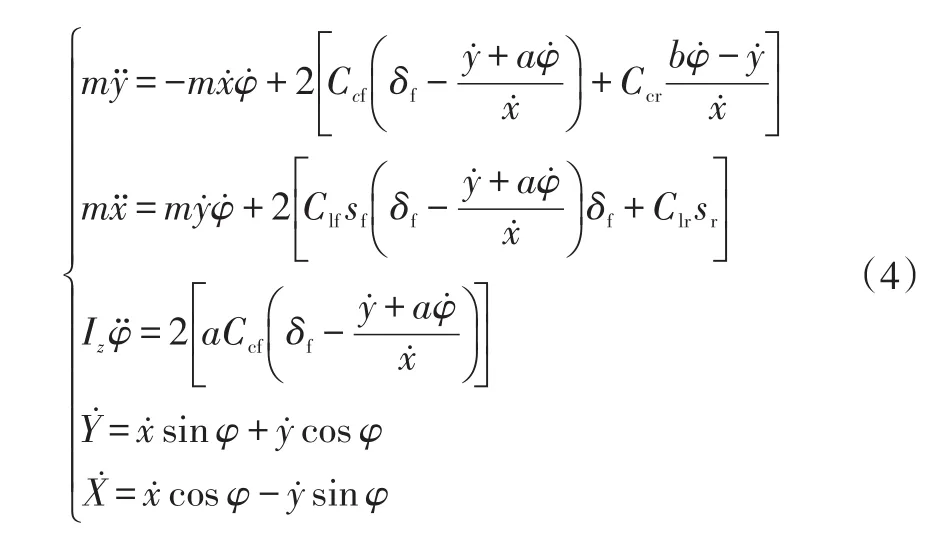
式中，Ccf、Ccr分別為車輛前、后輪側偏剛度；Clf、Clr分別為車輛前、后輪輪胎縱向剛度；δf為前輪偏角；sf、sr分別為前、后輪滑移率；X、Y分別為慣性坐標系坐標下車輛坐標。

2.2 模型線性化

由于智能車在高速行駛過程中對車輛運動控制器實時性要求很高，非線性模型預測控制難以滿足，因此，在參考點進行泰勒展開并只保留一階項，將車輛的動力學模型線性化。

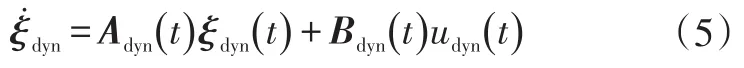
2.3 狀態空間方程轉換

線性化得到的空間狀態方程中，udyn（t）是車輛的控制量，以這種形式的空間狀態方程得到的預測方程并不能對車輛控制量的增量進行有效的約束，因此還需要對上一節線性化后的空間狀態方程進行進一步轉換。

本文取狀態變量

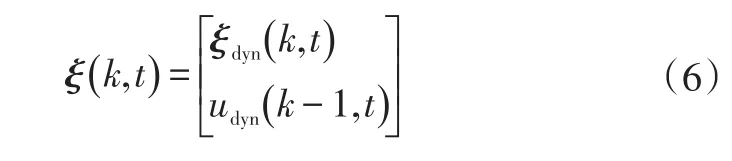
結合式（5）和式（6），可以得到新的狀態空間方程：

3 模型預測控制器

模型預測控制器作為車輛路徑跟蹤的決策機構，通過狀態采集器獲取上一時刻車輛狀態，通過預測模型對車輛預測時域內的狀態進行預測，構建二次型目標函數，并結合約束條件，優化求解得到控制時域內各個周期的控制量，最后將控制序列的第一個元素作用于車輛，在下一個采樣時刻重新獲取車輛的狀態，繼續進行下一輪的滾動優化[8]。智能車模型預測控制原理如圖2所示。

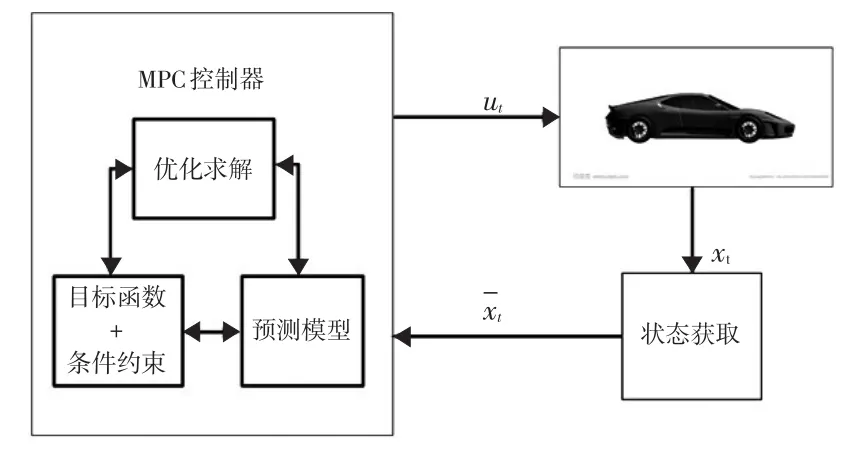
圖2 模型預測控制原理

3.1 目標函數設計

在智能車的目標路徑跟蹤中，目標函數的作用是使其準確、快速地跟隨目標路徑。因此，目標函數必須包含系統的狀態量和控制量。參考文獻[4]，目標函數為：

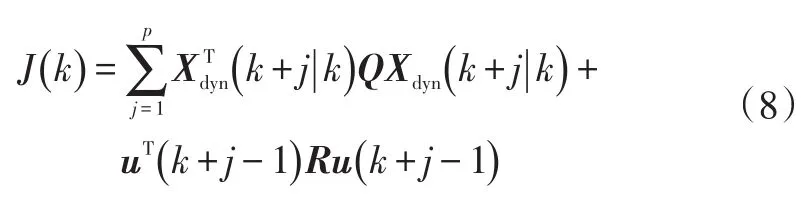
式中，Xdyn為狀態量；Q為狀態加權矩陣；u為輸入控制量；R為控制加權矩陣；P為預測時域。

該形式的目標函數使用系統狀態量和控制量進行優化求解，當系統使用動力學空間狀態模型時，由于約束量較多，會導致系統計算時間成本過高，而直接使用系統控制量來進行約束也會導致無法對控制增量進行有效約束[9]。因此，本文采用的模型預測控制器目標函數為：

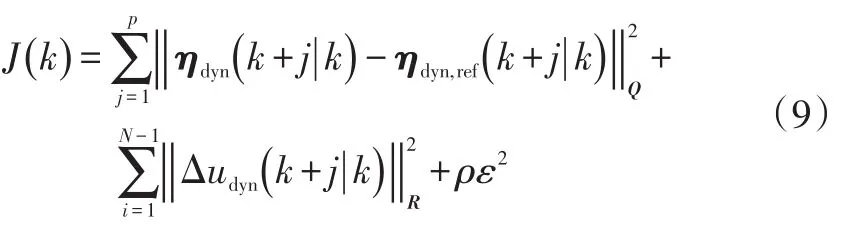
式中，ηdyn為輸出量；ηdyn,ref為輸出量參考量；Δudyn為控制偏差增量；ρ為松弛因子權重系數；N為控制時域。

由于使用的是車輛動力學模型，并且增加了約束條件的數量，為了避免無最優解情況的出現，為目標函數添加了松弛因子ε[10]。

結合式（7）和式（9），消除系統狀態量ξ（k,t）可得：

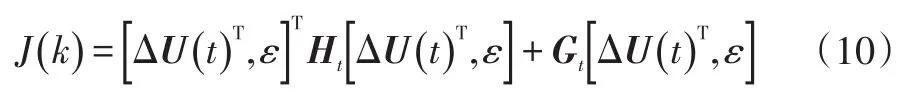
3.2 條件約束

模型預測控制最突出的特點就是能很方便地處理多約束問題[11]，為了保證智能車平穩地跟蹤目標路徑，本文采用前輪偏角約束、前輪偏角增量約束以及輪胎側偏角動力學約束。

3.2.1 前輪偏角及其增量約束

對于車輛的前輪偏角和前輪偏角增量的約束，可以根據車輛的實際物理參數進行設置。控制量約束表達式為：

控制增量約束的表達式為：

在目標函數以及約束條件中，被優化變量為控制時域內的控制增量，因此，控制量要首先轉化為Δu的矩陣形式。

由控制增量和控制量的關系可得：

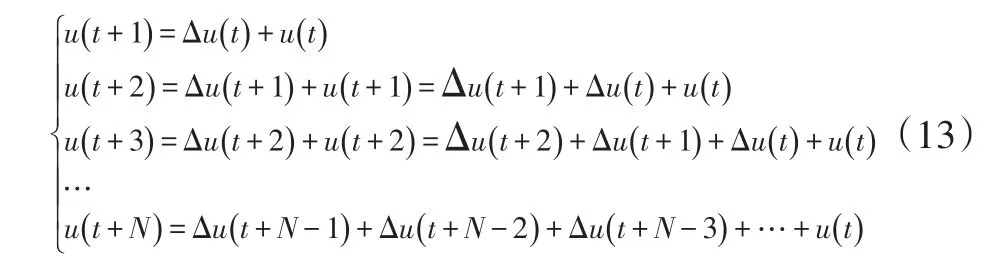
將式（11）轉化為Umin≤A?U+Ut≤Umax的形式，其中，

控制量和控制增量的約束能夠保證模型預測控制器生成的控制輸出是物理可實現的，但為了保證智能車在道路上的平穩、安全行駛，還需要增加車輛的動力學約束。

3.2.2 輪胎側偏角動力學約束

智能車在行駛時，可能因路面濕滑或者轉彎過急而導致車輛發生側滑，進而引發各種事故。因此，增加車輛動力學約束、降低車輛發生側滑的可能性尤為重要。

[12]可知，車輛的側滑和輪胎側偏角密切相關。當車輛在水平道路直線行駛時，輪胎側偏角α=0；當輪胎受到橫向的力發生彈性形變而未發生側滑時，α≤αmax；當輪胎受到橫向的力過大而導致車輛側滑時，α＞αmax。由此可以得出，車輛輪胎的側偏角直接反映了車輛是否發生側滑，限制了輪胎側偏角就限制了側滑的發生。

而由于建立的車輛動力學空間方程并沒有將輪胎側偏角作為狀態量，無法對輪胎側偏角進行直接約束，所以本文需要尋找輪胎側偏角與狀態量ξ（k,t）之間的關系，通過對狀態量施加特定關系的約束來達到約束輪胎側偏角的目的。

由車輛動力學模型中各速度之間的關系可得輪胎側偏角為：

式中，vc和vl分別為輪胎的橫向和縱向速度。

vc和vl又可以通過車輛坐標系的速度vx和vy來表示：

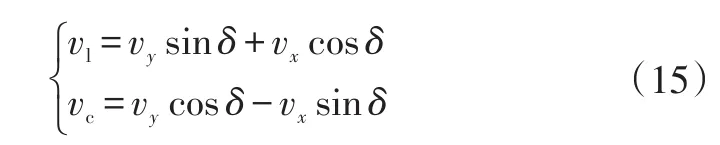
但由于vx和vy仍然不是系統的狀態量，因此還要經過轉換：

式中，vxf、vxr、vyf、vyr分別為車身坐標系下前、后輪x方向速度以及前、后輪y方向速度。

對式（14）～式（16）進行簡化和合并，可得輪胎前、后輪側偏角為：

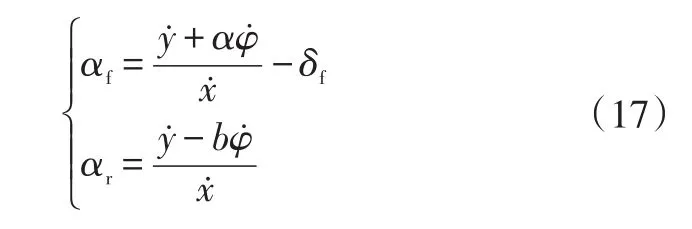
以ξdyn為狀態量，以udyn為控制量，對上式進行線性化，可得：

式中，α=[αfαr]T為輪胎側偏角矩陣；F=[-1 0]T為直接傳遞矩陣；為輸出矩陣。

對式（18）進行空間轉換，可得：

綜合以上目標函數和約束條件，基于動力學模型預測控制器的優化問題可描述為：

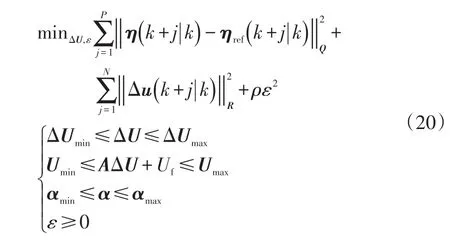
對于式（20）的優化問題，可以轉換為二次規劃的問題[13]，由于優化問題的約束條件都是不等式約束，因此二次規劃的問題采用有效集方法便可以得到優化問題的最終可行解。

4 仿真驗證

為了測試改進模型預測控制的智能汽車路徑跟蹤方法的效果，在以CarSim與MATLAB/Simulink構建的聯合仿真平臺上進行了仿真驗證。

4.1 仿真平臺設計

該仿真平臺由CarSim提供車輛動力學模塊，通過MATLAB語言編寫S函數作為系統控制器，在Simulink中進行整體結構的搭建。仿真平臺系統結構如圖3所示。

圖3 仿真系統結構

本文CarSim車輛動力學模型以北京工業大學BJUT-IV無人駕駛車輛平臺為原型。通過測量，該車整車質量為680 kg；質心與前、后軸的距離分別為1 250 mm和1 000 mm；質心高度為540 mm；輪距為1 230 mm；滾動阻力系數為0.015；空氣阻力系數為0.8（電動觀光車外形）。

為有效檢驗控制算法的動力學性能，跟蹤路徑選擇雙移線曲線，雙移線曲線測試是國際標準的車輛穩定性能的測試項目，也被稱為動態翻滾測試，是包括轉向角快速逆轉的激烈轉向路線測試，以雙移線作為測試跟蹤路徑，能更好地檢測控制算法的穩定性[14]。雙移線曲線如圖4所示。

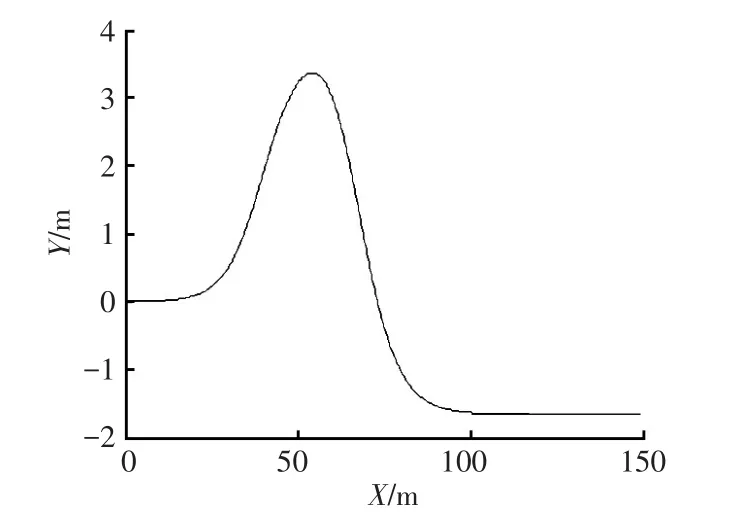
圖4 雙移線曲線

4.2 仿真方法及結果

4.2.1 有、無輪胎測偏角約束對比驗證

為了驗證改進模型預測控制的智能車路徑跟蹤方法在濕滑道路狀況下的控制效果，對有輪胎側偏角約束和無輪胎側偏角約束的兩種控制方法進行了3組對比仿真。

3組對比仿真均以道路附著系數為變量，在車速（15 m/s）、參考路線（雙移線）等條件都相同的情況下，探究有車輪側偏角約束控制器和無車輪側偏角約束控制器時的行駛效果。

由文獻[6]可知，車輛正常行駛的干燥道路附著系數的取值范圍為0.7～1.0，濕滑道路的附著系數約為0.4，因此在仿真中，為符合道路實際情況，設置道路附著系數范圍為0.3≤μ≤0.8。

分別設置路面附著系數為0.8、0.5、0.3，添加和未添加輪胎側偏角約束的仿真結果如圖5所示。

由圖5可知：當道路附著系數為0.8和0.5時，由于道路附著條件相對較好，車輛均能夠很好地跟隨參考軌跡，車輛的前輪側偏角小于0.15°，有、無車輪側偏角約束曲線基本重合。

當道路附著系數為0.3時，道路附著條件已相對較差。由圖5a中μ=0.3無車輪側偏角約束的位移曲線可知，試驗車輛在x=50 m附近轉過第1個急彎之后，由于道路較為光滑，出現了比較嚴重的側滑現象，而有車輪側偏角約束的位移曲線相對更好地跟蹤了目標軌跡。在x=100 m附近，未進行輪胎側偏角約束的車輛由于路徑偏差過大，逐漸失去了路徑跟蹤能力，發生車道偏離，而有輪胎側偏角約束的車輛通過對車輛的控制，目標路徑跟蹤偏差在x=175 m附近減小為零。由圖5b中μ=0.3對比曲線可知，在約第6 000個控制周期時，無輪胎側偏角約束的車輛的由于轉彎不當，導致車身在濕滑的道路上發生旋轉，側偏角偏差不斷增大，車輛失去控制能力，而有輪胎側偏角約束的車輛在車頭左右擺動之后，航向角偏差逐漸減小為零。由圖5c中μ=0.3的對比曲線可知，在開始階段，無輪胎側偏角約束的車輛側滑程度較有輪胎側偏角約束的車輛大，車輛仍處于可控階段，而在后半段，開始發生嚴重的側滑，處于不可控狀態。有輪胎側偏角約束的車輛在急速轉向時發生了側滑，但側偏角度始終未超過0.5°，隨后進入平穩路段，側偏角度逐漸減小為零。

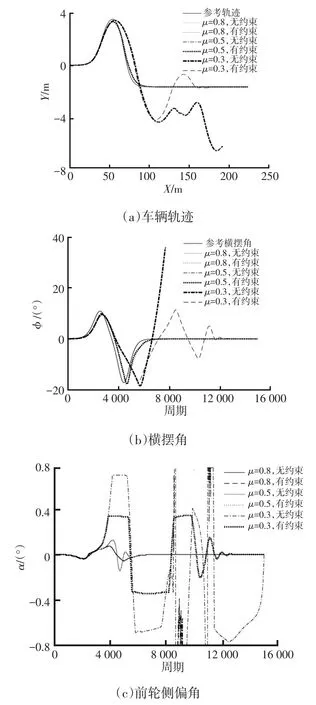
圖5 仿真結果

4.2.2 車輛速度對比仿真

為了檢驗基于改進模型預測控制的智能汽車路徑跟蹤方法對于車速的魯棒性以及控制算法的實時性，采用接近正常行駛路面的附著系數為0.8的道路，在其它條件都相同的條件下，使車輛分別以10 m/s、20 m/s、25 m/s的速度在雙移線道路行駛，觀察車輛的跟蹤性能以及控制算法消耗的時間。

不同車速下車輛的行駛軌跡如圖6所示。由圖6可以看出，車輛在10 m/s、20 m/s車速工況下可以較好地跟隨目標路徑，當行駛速度為25 m/s時，雖然出現較大的側滑導致跟蹤出現偏差，但車輛仍處于可控狀態。

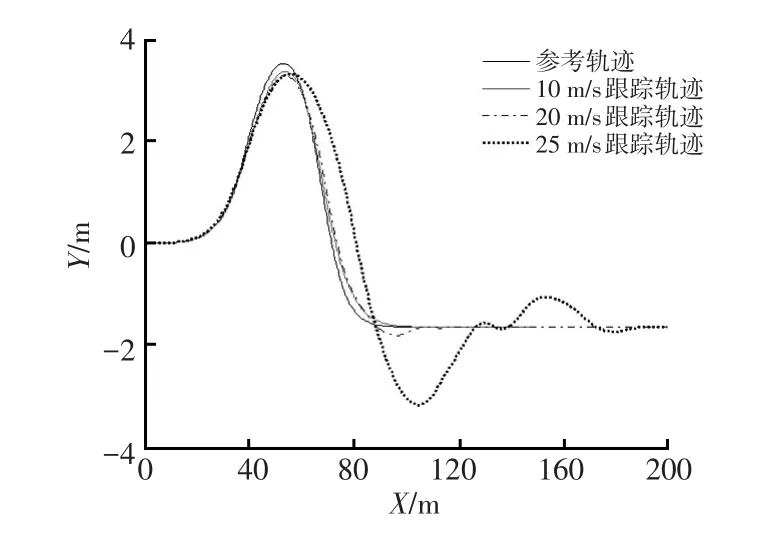
圖6 車輛軌跡

不同車速下控制算法消耗的時間如圖7所示。由圖7可知，不同車速條件沒有很大程度影響控制算法耗時間。除1個特殊控制周期外，控制算法消耗的時間大部分在13～25 ms范圍內。

圖7 計算時間

5 結束語

本文提出的智能汽車路徑跟蹤方法不僅在道路附著系數較高時能夠有效降低輪胎側偏角，在道路附著系數較低時有效減輕車輛側滑程度，降低智能汽車目標路徑跟蹤時因跟蹤偏差過大導致失控情況發生的幾率，而且在不同車速下都有較好的跟蹤效果，具有速度的魯棒性，同時具有良好的實時性。

下一步將繼續改進模型預測控制的目標函數，簡化算法的復雜度，并引入對解算時間的監控，避免出現個別周期過長的情況；同時將考慮引入乘客舒適度約束，提高智能車路徑跟蹤的舒適性和實用性。

參考文獻

1 Jonathan B,Tully F,Jim K,et al.Little Ben:The Ben Franklin Racing Team's Entry in the 2007 DARPA Urban Challenge.Journal of Field Robotics，2008，25（9）：598～614.

2 Urmson C,Ragusa C,Ray D,et al.A Robust Approach to High-Speed Navigation for Unre-Hearsed Desert Terrain.Journal of Field Robotics，2006，23（8）：467～508.

3 Akeb H,Hifi M.Solving the Circular Open Dimension Problem by Using Separate Beams and Look-Ahead Strategies.Computers and Operations Research，2013，40（5）：1243～1255.

4 Kühne F,Fetter W,Jo?o L,et al.Model Predictive Control of a Mobile Robot Using Lineariza-tion.Prodeedings of Mechatronics and Robototic，2004（4）：525～530.

5 孫銀鍵.基于模型預測控制的無人駕駛車輛軌跡跟蹤控制算法研究：[學位論文].北京：北京理工大學，2015.

6 龔建偉，姜巖，徐威.無人駕駛車輛模型預測控制.北京：北京理工大學出版社，2014.

7 劉洋.基于模型預測控制的移動機器人路徑跟蹤控制：[學位論文].長春：吉林大學，2016.

8 Gong J,Xu W,Jiang Y.Multi-constrained Model Predictive Control for Autonomous Ground Vehicle Trajectory Tracking.Journal of Bering Institute of Technology，2014，24（4）：441～448.

9 席裕庚，李德偉，林姝.模型預測控制現狀與挑戰.自動化學報，2013，39（3）：222～236.

10 李升波，王建強，李克強.軟約束線性模型預測控制系統的穩定性方法.清華大學學報，2010，50（11）：1848～1852.

11 陳虹.模型預測控制.北京：科學出版社，2013.

12 付聰.輪胎側傾側偏極限工況力學特性研究：[學位論文].長春：吉林大學，2013.

13 周晶晶，徐友春.基于改進的QP算法和MPC理論的智能車縱向速度控制方法.軍事交通學院學報.2016，18（10）：49～53.

14 Falcone P.Nonlinear model Predictive Control for Autono?mous Vehicles：[dissertation].Benevento：Universitadel Sannio，2007.

（責任編輯 斛 畔）

修改稿收到日期為2017年5月9日。

Research on Target Path Tracking Method of Intelligent Vehicle Based on Model Predictive Control

Duan Jianmin,Tian Xiaosheng,Xia Tian,Song Zhixue
（Beijing University of Technology,Beijing 100022）

To avoid the occurrence of vehicles’side-slip and improve the performance of automatic drive during target path tracking,an improved intelligent vehicle target path tracking method was proposed.In this proposed method,the vehicle dynamics model was used as the predictive control model,the objective function was improved and the dynamic constraint of the tire slip angle was added.This proposed method was validated on the co-simulation platform constructed by CarSim and MATLAB/Simulink.The results show that the proposed method can reduce the probability of side-slip during target path tracking,and improve the tracking accuracy and safety of the intelligent vehicle target path tracking.

Intelligent vehicle,Target path tracking,CarSim/Simulink co-simulation,Model predictive control

智能汽車 目標路徑跟蹤 CarSim/Simulink聯合仿真 模型預測控制

U467.1 文獻標識碼：A 文章編號：1000-3703（2017）08-0006-06

北京市屬高等學校人才強教計劃資助項目（038000543117004）。