三角形綜合問題一題多解
?湖北省黃岡市團風中學 林菊芳
1 引言
從近幾年的高考試題來看,解三角形問題成為高考的高頻考點.主要考查運用正、余弦定理及其他相關的變形公式解決與三角形有關的證明、求面積、判定三角形形狀等問題;題型多樣,既有填空題、選擇題,也有簡答題和綜合應用題,側重考查計算能力和分析問題、解決實際問題的能力[1].下面是筆者總結的幾種解題的方法與技巧,供大家參考.
2 三角形證明題“兩要”法
三角形中的證明類問題,其基本思路和方法與證明三角恒等式類似.證明的要領可歸納為“兩要”:一要“轉化”,變陌生為熟悉,就是運用正、余弦定理使原來混合的邊、角關系統一為邊的關系或角的關系,將其轉化為我們熟悉的三角恒等式類的證明問題,或將其轉化為代數恒等式類的證明問題;二要靈活運用三角形中的相關結論(公式、定理),例如
sin(B+C)=sinA,cos(B+C)=-cosA,
例1在△ABC中,已知acosA=bcosB,求證:△ABC為等腰三角形或直角三角形.
證法1:從角入手進行證明.
在△ABC中,由acosA=bcosB,得2RsinA·cosA=2RsinBcosB,即sin 2A=sin 2B.
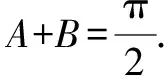
所以,△ABC為等腰三角形或直角三角形.
證法2:從邊入手進行證明.
在△ABC中,由acosA=bcosB,得
整理,得c2(a2-b2)=a4-b4.
即c2(a2-b2)=(a2-b2)(a2+b2).
于是 (a2-b2)[c2-(a2+b2)]=0.
所以a=b,或c2=a2+b2.
故△ABC為等腰三角形或直角三角形.
例2在△ABC中,求證:sin2A+sin2B-sin2C=2sinAsinBcosC.
證法1:因為
sin2A+sin2B-sin2C
=cos2(A+B)-cos(A+B)cos(A-B)
=cos(A+B)[cos(A+B)-cos(A-B)]
=-cosC(-2sinAsinB)=2sinAsinBcosC,
所以,原等式得證.
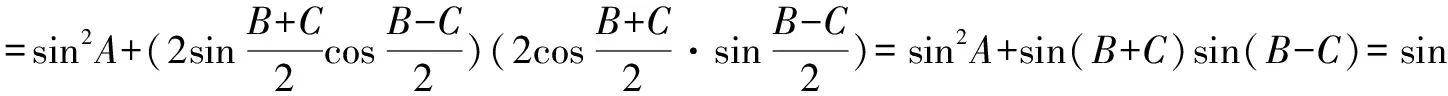
所以,原等式得證.
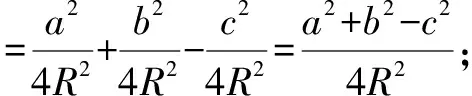
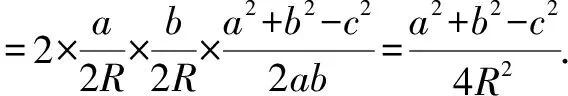
所以,左邊=右邊,故原等式得證.
3 運用“轉化法”判斷三角形的形狀
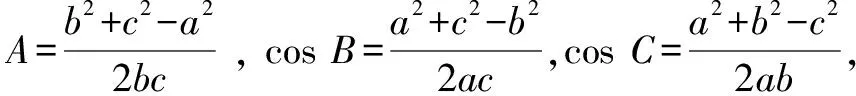
例3在△ABC中,若B=60°,2b=a+c,試判斷△ABC的形狀.
解法1:由正弦定理,得2sinB=sinA+sinC.
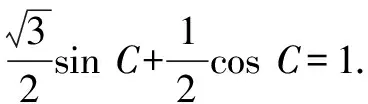
即sin(C+30°)=1.
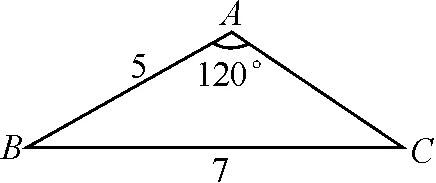
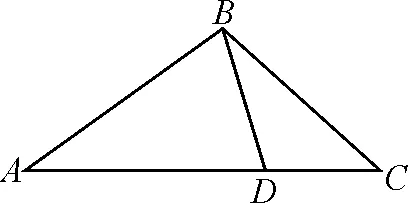
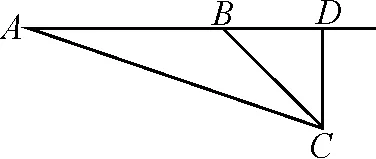
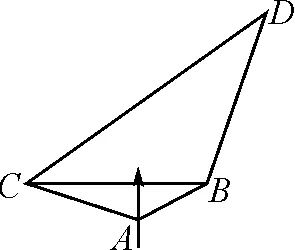
因為0° 于是A=60°=B=C. 故△ABC為正三角形. 解法2:由余弦定理,得b2=a2+c2-2accosB. 整理,得(a-c)2=0,即a=c,從而a=b=c. 故△ABC為正三角形. 例4在△ABC中,已知b2sin2C+c2sin2B=2bccosBcosC,試判定△ABC的形狀. 8R2sin2Bsin2C=8R2sinBsinCcosBcosC. 因為sinBsinC≠0,所以sinBsinC=cosBcosC. 于是cos(B+C)=0,則B+C=90°,所以A=90°. 故△ABC為直角三角形. 解法2:將已知等式變為 b2(1-cos2C)+c2(1-cos2B)=2bccosBcosC. 化簡得b2+c2=a2. 故△ABC為直角三角形. 其次,針對不同的題型和具體要求,靈活地選用或變形使用三角形面積公式. 例5在△ABC中,已知A=120°,AB=5,BC=7,求△ABC的面積. 圖1 圖2 例6某職業中專校園背后有一塊形似三角形的學農基地(如圖2),AB邊長為20 m,由點C看AB的張角為40°,在AC上的另一點D處看AB的張角為60°,已知AD=2DC.試求這塊學農基地的面積(精確到0.1 m2). 解:依題意可知∠BCA=40°,∠BDA=60°, 則∠DBC=20°,∠BDC=120°.設DC=x. 在△ABC中,AB=20,利用余弦定理可知 AB2=AC2+BC2-2AC×BC×cosC. 即400=(3x)2+(2.53x)2-2×3×2.53x2cos 40°. 解得x≈10.3,從而AC=30.9,BC≈26.03. 故這塊學農基地的面積約為257.4 m2. 求解高度與追擊問題,大多要利用正、余弦定理,聯系高度、距離所在的某個三角形,弄清方向角、方位角,將有關角的關系進行綜合應用,觀察和求出所在三角形中的某些邊、角,當條件不夠時,需要創造和尋找條件[3],將有關條件向該三角形轉化,最終化為解三角形的問題. 圖3 解:由A=15°,∠DBC=45°,可得∠ACB=30°. 因為CD⊥AD,所以 CD=BCsin∠CBD ≈10 500(1.7-1) =7 350(m). 故山頂的海拔高度為10 000-7 350=2 650 (m). 圖4 在△ABC中,∠BAC=45°+75°=120°,則 BC2=AB2+AC2-2AB×AC×cos∠BAC =6. 由正弦定理,得 所以∠ABC=45° ,且BC為東西走向. 由題意可知∠CBD=120°. 在△BCD中,由正弦定理,得 所以∠BCD=30°. 于是∠BDC=30°. 綜上所述,解三角形問題的關鍵是要準確理解三角形中的邊角關系,會嫻熟地運用相關的公式、定理;對于實際應用題,最好能夠運用數形結合思想,通過構圖、作輔助線等方法幫助分析、思考問題.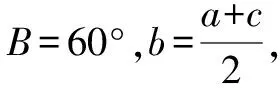
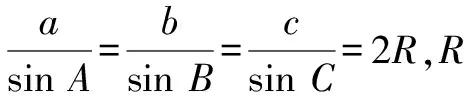
4 巧用公式求三角形的面積.
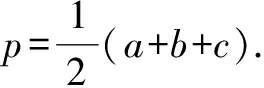
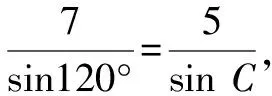
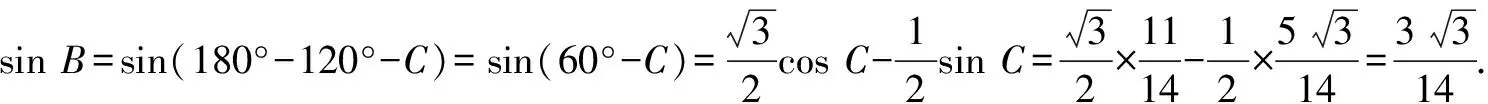
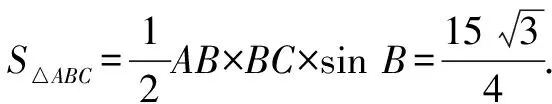
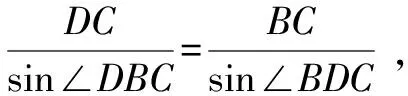
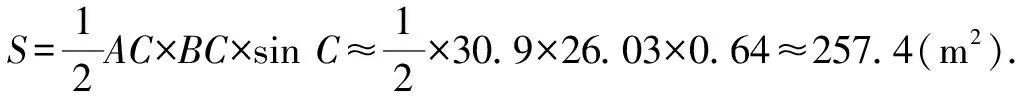
5 活用正、余弦定理求解高度與追擊問題
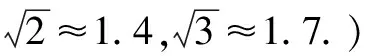
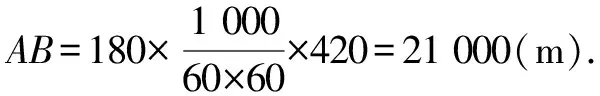
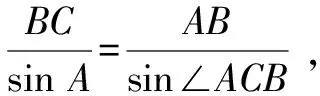
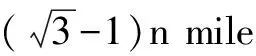
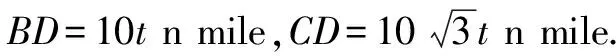
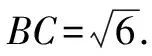
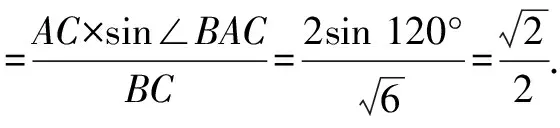
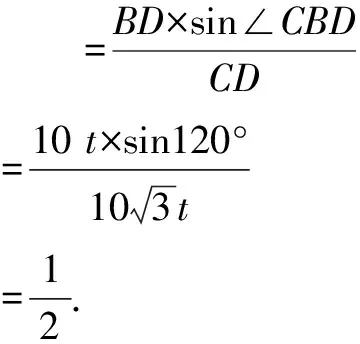

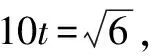
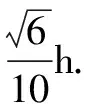
6 結論

