面向空域和機動性的攔截彈能量管理優化研究*

賈懌，譚湘霞

(北京電子工程總體研究所，北京 100854)

面向空域和機動性的攔截彈能量管理優化研究*

賈懌，譚湘霞

(北京電子工程總體研究所，北京 100854)

研究了攔截彈能量管理優化問題，通過分配攔截彈的第3級雙脈沖固體發動機推進劑裝藥量，使攔截彈的作戰空域和機動性綜合最優。首先建立了攔截彈質量和動力模型，然后提出了攔截彈空域、全彈和第3級Ⅱ脈沖機動性分別最大的單目標優化模型，以及其綜合性能最優的多目標優化模型。最后采用粒子群優化算法，面向攔截彈空域和機動性，對第3級雙脈沖裝藥量分配進行了優化及分析。

攔截彈；空域；機動性；雙脈沖能量優化；粒子群算法；多目標優化

0 引言

地基中段防御(ground- based midcourse defense，GMD)系統作為美國戰略反導系統的關鍵組成[1]，大空域、高機動性是其作戰能力的重要技術指標[2]。本文將GMD系統中地基攔截彈(ground based interceptor，GBI)的第3級單脈沖固體發動機用雙脈沖代替[3]，采用粒子群優化算法，希望尋求到一種能夠優化攔截空域和機動性指標的導彈能量管理方案。

本文所研究的對象是一枚采用三級助推的攔截彈，其中第3級分為2個脈沖。優化的重點為第3級雙脈沖的裝藥量分配。本文以動力學模型為基本方程[4]，基于兩脈沖裝藥量建立質量和動力模型，然后以大空域和高機動性分別為目標建立起單目標優化模型，并在此基礎上建立起多目標優化模型。采用粒子群算法進行優化，得到優化結果。最后針對不同權重系數的多目標優化模型進行了GBI攔截彈的第3級雙脈沖能量管理優化分配與仿真分析。

1 攔截彈質量和動力模型建立

為了進行攔截彈雙脈沖裝藥量分配的優化設計，首先要建立起質量和動力系統模型[5]。

本文的模型為串聯式三級彈，導彈總質量(起飛質量)為[6]

(1)

式中：M1，M2，M3為導彈第1，2，3級的質量，單位kg。其中，第3級總質量與裝藥量相關，具體計算如下：

(2)

式中：M3為第3級總質量；Msb為戰斗部與彈上設備質量；Mpr為推進劑質量；Men為發動機結構質量；Mb為彈體結構質量。

發動機推力

(3)

根據兩脈沖推進劑質量，結合質量流量和比沖，可以推出第3級總質量和兩脈沖推力。由此建立的導彈的質量和發動機推力隨時間變化曲線分別如圖 1， 2所示。

圖1 導彈質量變化示意圖Fig.1 Illustration of missile quality variation

圖2 導彈各級發動機推力變化圖Fig.2 Illustration of missile engine thrust variation

其中，第2，3級間滑行時間、第3級兩脈沖間滑行時間以及第3級兩脈沖燃燒時間是可調的，其大小由下文的優化設計來確定。

2 單目標優化設計模型

本文優化的重點是使攔截彈空域和機動性最大的第三級兩脈沖裝藥量的分配。

2.1 空域評價函數

本文空域是基于彈道仿真來計算的[7]。以預定的方案制導，同時仿真出多條不同飛行方案的彈道，由此得到該彈的空域。

三級+雙脈沖攔截彈空域的確定是一個兼顧飛行時序、飛行程序角的復雜過程。不同的級間滑行時間和飛行程序角都會影響空域分布。固定飛行時序，調整多條彈道的程序轉彎角，可確定空域[8]。對于本文的優化來說，該方法能夠客觀評價該裝藥量分配下的攔截空域的大小[9-10]。

空域評價函數為

(4)

式中：Jky為空域評價函數值；Ryuan為地面航程最大值；Hyuan為高程最大值；Rjin為地面航程最小值；Hjin為高程最小值。

該空域評價函數是以攔截彈飛行的高、遠、低、近界圍成的矩形面積來描述這型彈的空域特性。經測試，對于優化設計，該函數能夠客觀評價當前導彈參數下的空域大小。

2.2 機動性評價函數

本文以導彈能提供的理想速度增量來評價導彈機動性，速度增量和發動機推進劑比沖及質量之間的關系通常用齊奧爾柯夫斯基公式表示[11]，故全彈機動性評價函數為

(5)

式中：Jzd為全彈機動性的評價函數值；Mt0，Mt1分別為導彈初始質量、第1級燃燒結束后質量；Mt20，Mt2分別為第2級初始質量、第2級燃燒結束后質量；Mt30，Mt31，Mt32分別為第3級初始質量、第3級Ⅰ脈沖燃燒結束后質量(第3級Ⅱ脈沖段初始質量)、第3級Ⅱ脈沖燃燒結束后質量；Isp1，Isp2，Isp31，Isp32分別為第1級、第2級、第3級Ⅰ脈沖和Ⅱ脈沖的比沖。

本文還將關注第3級雙脈沖能量分配對Ⅱ脈沖機動性的影響，則有

(6)

式中：Jem為第3級Ⅱ脈沖機動性的評價函數值。

2.3 參數優化模型

本文選定的目標為攔截彈的空域最大、全彈機動性最大、Ⅱ脈沖機動性最大，即maxJky，maxJzd，maxJem。

本文選擇如下參數進行優化：

第3級Ⅰ脈沖燃燒時間T31，

第3級Ⅱ脈沖燃燒時間T32。

因此，上述優化目標函數可分別寫為

從工程實際要求出發確定了約束條件，主要包括

(1) 二級關機點速度：v二級關機≥v2jmin；

(2) 導彈飛行末速：v末速≥vmsmin；

(3) 戰斗部滑行距離L戰斗部≥Lzmin，

式中：v2jmin，vmsmin，Lzmin分別為二級關機點、導彈飛行末速、戰斗部滑行距離的約束邊界值。

將上述約束變形為gi(x)≥0的形式，采用“外罰函數法”對不等式約束進行處理，引入“懸崖代價函數”得到無約束代價目標函數

式中：

(7)

k為懲罰系數，本文取k=1 000；J0為未加約束的評價函數。

由此可得導彈總體參數優化模型為：在約束條件gi(x)≥0下，分別尋找一組T31，T32值使攔截彈的空域、全彈機動性、Ⅱ脈沖機動性評價函數值Jky，Jzd，Jem最大。其中gi(x)滿足

(8)

2.4 粒子群優化算法

粒子群優化算法(particle swarm optimization，PSO)是對參數優化算法中的現代啟發式算法的一種。作為群智能算法中的一支代表，粒子具有全局搜索的性能[12]。粒子在解空間內通過相應的適應度值，來動態更新粒子的狀態，使其追隨最優粒子搜尋到最優解。

假設在一個D維的目標搜索空間內，粒子群由N個代表問題潛在解的粒子組成[13]。利用速度和位置向量來綜合表示每個粒子的狀態。用xi(t)=(xi1，xi2，…，xiD)和vi(t)=(vi1，vi2，…，viD)向量來表示粒子i在D維搜索空間內的位置和速度。粒子在每次進化更新過程中，通過跟隨個體極值和全局極值來更新自身的狀態。其更新滿足如下公式：

(9)

(10)

式中：t為當前粒子更新自身狀態的迭代次數；c1，c2為加速因子。其中，c1是粒子自身學習因子而c2為社會學習因子，一般取c1= c2=1.499 4；r1，r2是介于[0，1]之間的隨機數；pbi，gb分別表示第i個粒子當前時刻的個體極值和全局極值。

(11)

(12)

式中：f(xi(t+1))為基于當前種群得出的粒子的適應度值；f(pbi(t))為自身歷史最優值。算法根據粒子的適應度值不斷更新粒子的pbi和gb，直至搜索到最優解所在的位置[14]。

3 多目標優化設計模型

本文的多目標優化模型是以單目標優化結果為基礎建立的，下面首先進行單目標優化計算分析，然后在此基礎上完成多目標優化模型建立和仿真分析。

3.1 單目標優化計算分析

首先以評價函數Jky，Jzd，Jem作為空域、全彈機動性、第3級Ⅱ脈沖機動性的優化目標函數，則優化的目標是使這3項最大。采用粒子群算法分別作單目標優化，結果如表1所示。

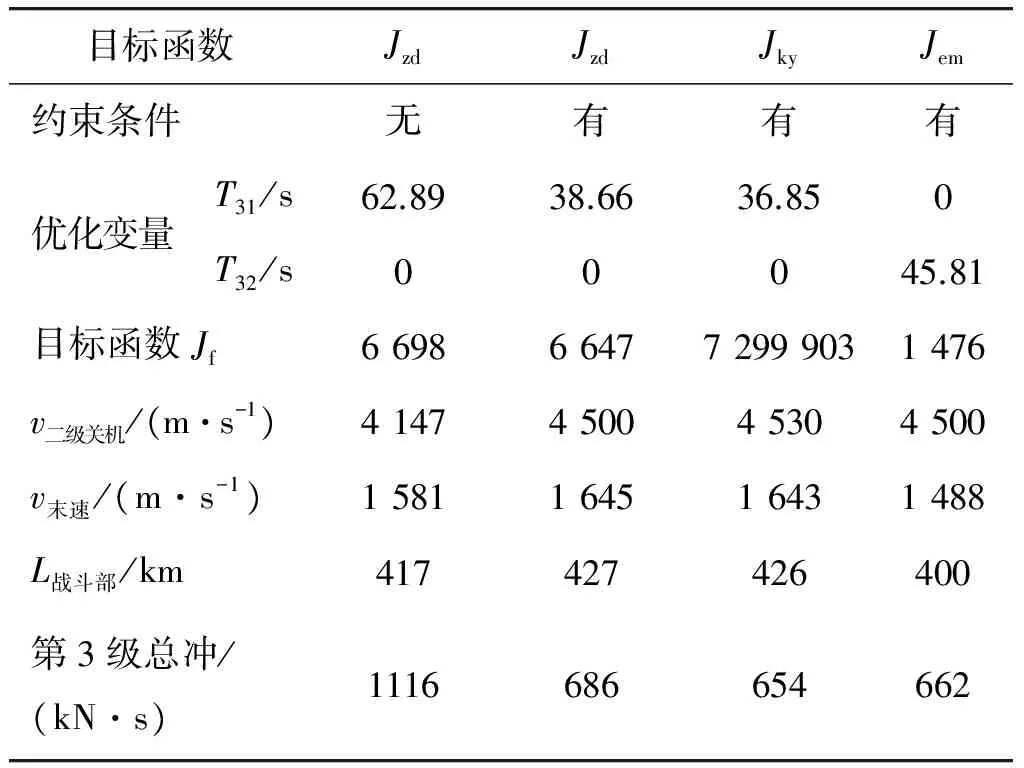
表1 優化設計結果

由上述優化設計結果即相關參數輸出值可以看出，不考慮工程實際約束條件時，當第3級總沖小于1 116 kN·s時，總沖越大，全彈機動性越大；第3級Ⅰ脈沖裝藥量對導彈空域影響更大，在一定范圍內，Ⅰ脈沖盡可能大，Ⅱ脈沖裝藥量盡可能小可使空域所覆蓋的區域更大；而Ⅱ脈沖發動機裝藥量越多可以使導彈Ⅱ脈沖機動性越強，軌道修正能力也越強。

3.2 多目標優化模型

多目標優化比單目標優化復雜，求解難度大，對于多目標優化問題，采用加權法能夠將多目標優化轉化為單目標優化問題來求解。文獻[15]提出了“規范化加權平方和法”來求解多目標優化的問題。具體闡述如下：若對目標函數J1，J2，J3進行多目標優化，先找到其最大值J1max，J2max，J3max，則經這種“加權法”處理后的綜合目標函數如下

(13)

式中：α1，α2，α3為3個子目標的權重系數，滿足條件α1+α2+α3=1。

針對“規范化加權平方和法”不能確保所有子目標值都在[0，1]區間內變化而導致各子目標變化范圍不同的缺點，本文提出“改進的規范化加權平方和法”。其原理為：若對子目標函數J1，J2，J3進行多目標優化，先找到J1，J2，J3的最大值J1max，J2max，J3max和最小值J1min，J2min，J3min。則經“改進的規范平方和加權法”處理后的目標函數為

(14)

式中：α1，α2，α3為3個子目標的權重系數，滿足條件α1+α2+α3=1。

根據上述方法，先找到空域Jky、全彈機動性Jzd、Ⅱ脈沖機動性Jem的最大、最小值如表 2所示。

表2 目標函數值

采用改進的規范加權平方和法建立優化目標函數：

(1) 以空域及全彈機動性最大為優化目標，權重系數αky=αzd=0.5，αem=0。其中αky，αzd，αem分別為空域、全彈機動性及Ⅱ脈沖目標函數的權重系數。則優化綜合目標函數為

(15)

(2) 以空域及Ⅱ脈沖機動性最大為優化目標，權重系數αky=αem=0.5，αzd=0，優化目標函數為

(16)

(3) 以空域、全彈機動性及Ⅱ脈沖機動性最大為優化目標，權重系數αky=0.4，αzd=0.2，αem=0.4，則優化目標函數為

(17)

(4) 仍以空域、全彈機動性及Ⅱ脈沖機動性最大為優化目標，權重系數為αky=0.3，αzd=0.3，αem=0.4，優化目標函數為

(18)

3.3 多目標優化計算分析

基于上述多目標優化模型，仍采用粒子群算法對本文提出的第3級為雙脈沖發動機的GBI攔截彈進行多目標優化，結果如表 3所示。

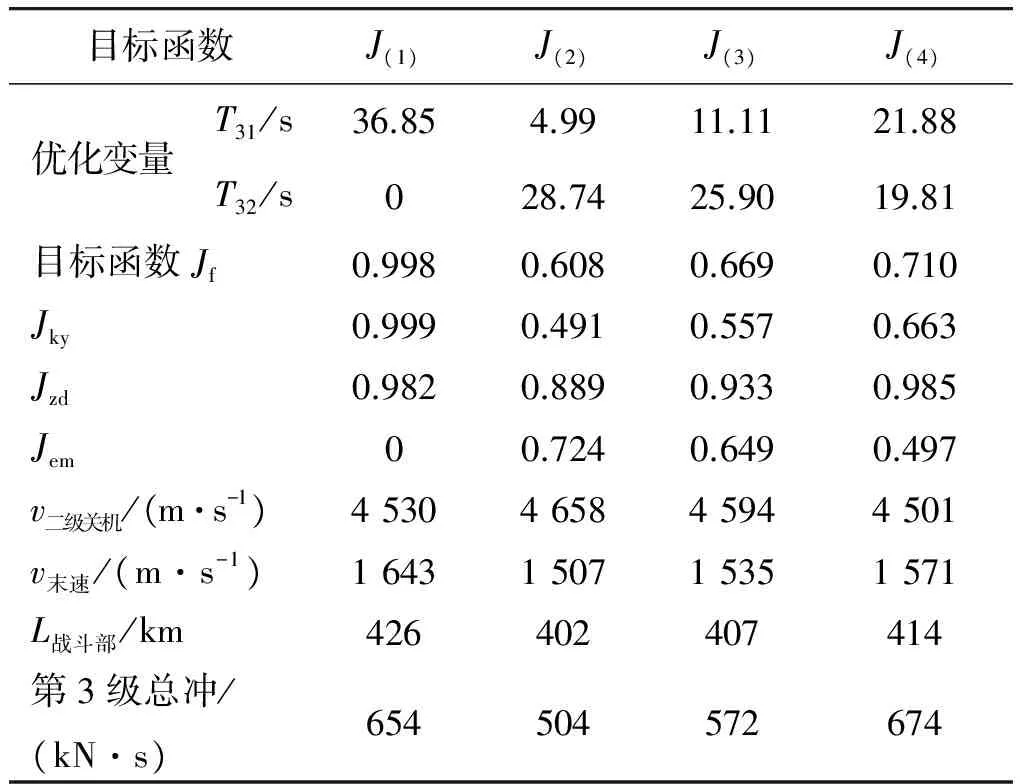
表3 優化設計結果

為便于比較，表3中Jky，Jzd，Jem為根據“改進的規范平方和加權法”處理后的值。

由表3的優化結果可以看出，在不同的權重下，攔截彈第3級Ⅰ，Ⅱ脈沖的裝藥量也隨之調整，以使空域、全彈機動性及Ⅱ脈沖機動性這3項性能指標綜合最優。

由上述的優化設計過程也可以看出，多目標優化問題中，各個子目標間可能是相互矛盾的，某一個子目標的改善，必然會引起另一個子目標性能的降低[16]。設計師們可以根據實際設計需要來調整各子目標的權重，以滿足其對各項優化目標的偏好程度。

4 結束語

本文針對攔截彈第3級雙脈沖裝藥量分配，建立起導彈質量模型和動力模型，進而面向空域最大和導彈機動性最強建立起導彈單目標優化模型，采用粒子群算法對雙脈沖裝藥量進行了優化設計，分析出裝藥量變化對優化目標的影響。基于單目標優化模型建立了綜合多目標優化模型。對于如何處理多目標優化的問題，本文提出了“改進的規范化平方和加權法”，用來反映工程設計中對各項指標的需求偏好，并得出綜合優化結果。

[1] 樊奇，馬春燕. 美國GMD系統攔截彈技術發展研究[J].現代防御技術，2016，44(4)：18-23. FAN Qi，MA Chun- yan. USA Ground- Based Kinetic Energy Interceptor Technology Development[J].Modern Defence Technology，2016，44(4)：18-23.

[2] 鮮勇，斯文輝. 對GMD系統攔截時機與空域的分析與研究[J].火力與指揮控制，2011，36(5)：192-194. XIAN Yong，SI Wen- hui. Study and Analyses of the Time and Airspace of Interception for National Missile Defense[J].Fire Control & Command Control，2011，36(5)：192-194.

[3] 李文杰. 美國中段反導系統發展分析[J].飛航導彈，2015(2)：41-46. LI Wen- jie. The Analysis About American Midcourse Missile Systems Development[J].Aerodynamic Missile Journal，2015(2)：41-46.

[4] 錢杏芳，林瑞雄，趙亞男. 導彈飛行力學[M]. 北京：北京理工大學出版社，2012. QIAN Xing- fang，LIN Rui- xiong，ZHAO Ya- nan，et al.Missile Flight Aerodynamics[M]. Beijing：Beijing Institute of Technology Press，2012.

[5] 張弫，鄭時鏡，于本水. 遺傳算法在遠程防空導彈總體優化設計中的應用[J].系統工程與電子技術，2003，25(1)：34-36. ZHANG Zhen，ZHENG Shi- jing，YU Ben- shui. Application of the Genetic Algorithms in the Optimization Design of the Long- Range Air- Defense Missile System[J].Systems Engineering and Electronics，2003，25(1)：34-36.

[6] 谷良賢，溫炳恒. 導彈總體設計原理[M]. 西安：西北工業大學出版社，2004. GU Liang- xian，WEN Bing- heng. Missile Overall Design Theory[M]. Xi’an：Northwestern Polytechnical University Press，2004.

[7] 趙健軍，李萬寶，桑德一，等. 基于彈道仿真的殺傷區計算[J].兵工自動化，2010，29(6)：8-15. ZHAO Jian- jun，LI Wan- bao，SANG De- yi，et al. Calculating Killing Zone Based on Trajectory Simulation[J].Ordnance Industry Automation，2010，29(6)：8-15.

[8] 李云，柳世考，殷業飛. 某小型地空導彈殺傷區仿真研究與分析[J].彈箭與制導學報，2006，26(2)：881-884. LI Yun，LIU Shi- kao，YIN Ye- fei. The Simulation Analysis and Research for Killing Scope of a Small Ground- to- Air Missile[J].Journal of Projectiles，Rockets，Missiles and Guidance，2006，26(2)：881-884.

[9] 韓品堯. 戰術導彈總體設計原理[M]. 哈爾濱：哈爾濱工業大學出版社，2000. HAN Pin- yao. Overall Design Theory of Tactical Missile[M]. Harbin：Harbin Institute of Technology Press，2000.

[10] 徐品高. 現代國土防空近程點防御防空導彈系統的發射區遠界和殺傷區遠界[J].現代防御技術，2008，36(6)：2-10. XU Pin- gao. Distant Boundary of Launching Zone and Kill Zone of the Short Range Air Defense Missile for Point Defense of Modern Territory Air Defense[J]. Modern Defence Technology，2008，36(6)：2-10.

[11] 賈沛然，陳克俊，何力. 遠程火箭彈道學[M]. 長沙：國防科技大學出版社，2009. JIA Pei- ran，CHEN Ke- jun，HE Li. Long- Range Rocket Ballistics[M]. Changsha：National University of Defense Technology Press，2009.

[12] 湯繼濤，戴月明. 全局智能優化算法的研究[D]. 無錫：江南大學，2014. TANG Ji- tao，DAI Yue- ming. The Research of Global Intelligent Optimization Algorithm[D]. Wuxi：Jiangnan University，2014.

[13] 邵雷，雷虎民，張建新，等. 基于微粒群算法的中制導彈道優化設計[J].彈道學報，2015，27(1)：7-11. SHAO Lei，LEI Hu- min，ZHANG Jian- xin，et al. Midcourse Guidance Trajectory Optimization Based on Particle Swarm Optimization Algorithm[J].Journal of Ballistics，2015，27(1)：7-11.

[14] 胡進海，史峰，萬春山. 基于粒子群算法的彈道導彈設計方法研究[J]. 微計算機信息，2009(13)：263-264. HU Jin- hai，SHI Feng，WAN Chun- shan. Ballistic Missile Design Method Study Based on PSO[J].Microcomputer Information，2009(13)：263-264.

[15] 孟婥，卜賀. 規范化加權平方和法多目標優化設計[J].哈爾濱科學技術大學學報，1995，19(5)：76-81. MENG Chuo，BU He. Normalized Weight- Square Method Multi- Object Optimization Design[J].Journal of Harbin University of Science and Technology，1995，19(5)：76-81.

[16] 馬小姝，王宇平. 多目標優化的遺傳算法研究[D]. 西安：西安電子科技大學，2010. MA Xiao- shu，WANG Yu- ping. Genetic Algorithms for Multi- Objective Optimization Problems[D].Xi’an：Xidian University，2010.

Interceptor Energy Management Optimization Oriented to Airspace and Mobility

JIA Yi，TAN Xiang- xia

(Beijing Institute of Electronic System Engineering，Beijing 100854，China)

The interceptor energy management optimization problem is studied. The airspace and mobility of interceptor is maximized by splitting the double pulse propellant of the third stage engine. The quality and dynamic model are established. The single object optimization model is proposed to maximize each of the airspace, the mobility of whole missile and the second pulse of the third stage. The multi- object optimization model is established to maximize the integrated performance of airspace and mobility. Oriented to airspace and mobility, the double pulse propellant split of the third stage is optimized by using particle swarm optimization (PSO) algorithm.

interceptor； airspace； mobility； double pulse energy optimization； particle swarm optimization (PSO)； multi- object optimization

2016-10-10；

2016-12-08 基金項目：有 作者簡介：賈懌(1991-)，男，山西太原人。碩士生，主要研究方向為飛行器設計。

10.3969/j.issn.1009- 086x.2017.04.012

TJ761.7；TJ760

A

1009- 086X(2017)- 04- 0071- 06

通信地址：100854 北京市142信箱30分箱 E- mail：xiaoyaohamigua@qq.com