多約束條件下戰時裝備維修任務分配方法

昝翔， 陳春良， 張仕新， 王錚， 劉彥

(裝甲兵工程學院 技術保障工程系， 北京 100072)

多約束條件下戰時裝備維修任務分配方法

昝翔， 陳春良， 張仕新， 王錚， 劉彥

(裝甲兵工程學院 技術保障工程系， 北京 100072)

針對現有戰時裝備維修任務分配中考慮約束條件不足、脫離實際的問題，以指派問題為基礎，建立裝備維修任務分配模型。該模型是在時間限制和維修能力限制的約束條件下，綜合考慮裝備修理時間、機動時間和維修能力的變化等因素，以修竣裝備的重要度之和最大為目標，進行維修任務分配的最優決策。同時設計一種兩階段啟發式算法，運用遺傳算法和鄰域搜索方法進行模型求解。通過算例和對比分析，驗證了該方法的合理性和有效性。

兵器科學與技術； 裝備維修任務分配； 多約束； 指派問題； 兩階段啟發式算法

0 引言

信息化條件下的戰時裝備維修任務呈現出數量多、類型復雜、時效性強的特點，因此對裝備維修系統提出了更高的要求。戰時裝備維修任務分配是裝備維修決策的重要內容，也是充分發揮戰時裝備維修系統效能的關鍵因素之一。

目前，關于裝備維修任務分配的研究大多集中在平時維修任務分配，目的是在保證裝備可靠性和安全性的前提下減小裝備維修費用。例如，Jia等[1]針對新型軍械裝備維修任務分配和保障資源需求問題，設計了計算機輔助決策系統，提高了維修工作效率。Chen[2]分析了維修任務分配的影響因素，運用區間模糊數解決任務分配過程中的不確定性和模糊性，構建了基于綜合平衡的維修任務動態分配模型。凌海風等[3]針對維修任務分配問題，提出多目標粒子群優化算法，以工程裝備大修計劃為例進行分析。關于戰時裝備維修任務分配的研究大多集中于維修任務在不同級別維修機構的縱向分配上。例如：Yuan等[4]運用蒙特卡洛仿真構建了維修任務分配模型，解決了戰時石油裝備維修任務分配問題；陳冰等[5]分析了人才成長率和裝備完好率對維修任務分配的影響，研究了維修任務在不同維修級別上的分配方法。隨著信息化技術的廣泛運用、戰場空間的擴展、部隊獨立作戰能力的增強，戰術級裝備維修需要發揮更加關鍵的作用。只有在規定時間內完成維修任務才能在作戰中發揮作用，同時由于作戰時間的縮短，使得戰術級往往不可能完成本級別所有的裝備維修任務，因此對裝備維修任務的合理取舍與劃分是發揮戰時裝備維修作用的關鍵。本文所述的戰時裝備維修任務分配指的是戰術級戰時裝備維修任務分配。

通過對戰時裝備維修任務分配的研究現狀分析，發現主要存在以下5個問題：

1)戰時維修任務分配研究中，對于維修任務縱向分配的研究較多，對維修任務在某一層次，尤其是戰術級上橫向分配的研究較少。

2)維修任務分配均以修復最大數量裝備或所用時間最短為決策目標，忽略了裝備體系中不同類型裝備對作戰的貢獻程度不同，應該增加考慮裝備重要度因素，以修復裝備的重要度之和最大作為決策目標，才能更好地發揮裝備維修對作戰的支持作用。

3)沒有充分考慮作戰時間對裝備維修的影響，超過時間限制修復的裝備不能對作戰做出貢獻，對于該次作戰屬于無效修復。

4)對于戰時裝備維修，機動巡回維修是裝備維修的主要形式，這就要求考慮裝備維修單元在不同待修裝備損壞位置之間機動的時間因素，這也是裝備維修任務分配的重要影響因素。

5)沒有考慮裝備維修單元能力下降的因素，由于維修資源的消耗和維修人員疲勞累積等原因，裝備維修單元的維修能力呈下降趨勢，必須充分考慮這一約束條件，才能使得維修任務分配模型更加符合實際。

針對以上問題，本文分析維修時間限制和維修能力限制，考慮裝備維修能力下降因素，以最大程度保證裝備體系完整性為目標，構建戰時裝備維修任務分配模型，設計兩階段啟發式算法進行求解，并通過算例驗證模型的合理性和有效性。

1 基本描述

1.1 概念描述

1)維修任務是裝備維修領域的一個常用概念，但是缺乏嚴格的定義。維修任務在文中的定義為：能夠使待修裝備恢復到繼續參加作戰的功能狀態所需的全部維修活動的總稱，一個維修任務對應一臺待修裝備。

2)在體系作戰的背景下，參戰裝備需要組成裝備體系，發揮整體作戰效能。裝備重要度指的是裝備在裝備體系中的重要程度，可以定量地反映裝備對作戰的貢獻。裝備重要度越大，對保持裝備體系的完整性就越重要。裝備重要度可以通過裝備在裝備體系中的重要度和裝備自身重要度兩個方面綜合評估獲得，受到多種因素的影響，會隨著裝備種類、作戰任務等因素的改變發生變化。

3)維修任務分配是指將維修任務劃分給裝備維修單元。維修任務分配的結果有兩個，即每個裝備維修單元所需完成的維修任務和完成維修任務的順序。維修任務分配是靜態劃分維修任務的過程，即在離散的時間點上對已出現的維修任務進行劃分。

4)裝備維修單元是戰時執行裝備維修任務的主體，由維修人員、維修裝備和設備以及相關的備品備件組成，具有一定的維修能力、機動能力和防護能力。

1.2 裝備維修任務分配描述

裝備維修任務分配是在裝備保障指揮機構通過信息偵察明確了維修任務相關信息的基礎上，以最大程度保持裝備體系的完整性為目標，在考慮時間與維修單元維修能力的基礎上，對維修任務進行合理劃分，明確各維修單元需要完成的維修任務及過程。裝備維修任務分配包含以下幾個要點。

1.2.1 前提條件

維修任務信息明確，即維修任務數量、工作量、待修裝備位置和裝備重要度等信息已經確定。

1.2.2 分配目標

裝備維修是為作戰服務的，以實現對作戰的最大支持為目標。為了完成該目標，需要提高修復裝備的數量，并且優先修復對作戰貢獻程度大的裝備。由于裝備重要度是裝備對作戰貢獻程度的定量反映，綜合上述兩個方面，裝備維修任務分配的目標設定為：修復裝備的重要度之和最大。

1.2.3 約束條件

1)時間限制：只有在限定時間內修復的裝備才能在本次作戰中繼續發揮作用，參考相關原則和作戰實際，本文設定時間限制為作戰時間的2/3，即只有在作戰時間的前2/3時間內完成的維修才能對本次作戰發揮支持作用。根據戰場實際情況，時間因素主要由兩個方面組成：待修裝備的修復時間和裝備維修單元到達待修裝備的機動時間。

2)維修能力限制：每個裝備維修單元所能承受的維修工作量有一個上限，所分配的工作量不能超過這個上限。考慮完成維修任務需要消耗維修資源并同時產生維修人員的疲勞累積等因素，裝備維修單元的維修能力隨時間呈下降趨勢。

1.3 假設描述

為了簡化問題、突出重點，做出如下假設：

1)待分配的維修任務均為本級有能力完成的維修任務。

2)維修任務在分配前已經明確裝備重要度、待修裝備修理時間以及待修裝備位置等信息。

3)忽略裝備修理時間的隨機性，采用平均修理時間表征裝備的修理時間。

4)忽略不同維修專業的影響，只要滿足維修工作量要求的待修裝備均可以修復。

5)在維修任務分配的過程中，不會出現新的維修任務。

6)只考慮修竣裝備對本次作戰任務的影響。

7)修復的裝備回原單位歸建，忽略歸建過程中所用的時間，即修復的裝備可立即回到原裝備體系繼續作戰。

8)不考慮敵方打擊對裝備維修單元維修能力的影響和對待修裝備的二次傷害。

2 模型建立

指派問題是指在一定約束條件下，將若干任務劃分給若干任務主體，如何使得效益最大或消耗最小的問題。文獻[6]中提到，該類問題于1955年由Kuhn提出，是整數規劃的一個分支。在軍事領域，目前被廣泛應用于火力打擊目標分配[7]、無人機任務分配[8]等問題。非平衡指派問題[9]是指派問題的一種特殊形式，主要用來解決任務與分配主體不平衡條件的指派問題。非平衡指派問題是一個非確定多項式時間可解問題(NP問題)，需要通過遺傳算法[10]、蟻群算法[11]、粒子群算法[12]等智能算法及優化方法求解。

裝備維修單元需要完成比自身數目多的維修任務，是一個典型非平衡指派問題，可參考非平衡指派問題的相關模型和求解方法解決維修任務分配問題。

2.1 參數定義

為了方便模型的描述，采用如下的參數定義:

1)tmax表示作戰持續時間。

2)I為維修任務集合，且|I|=n，n為維修任務的總數。

3)J為裝備維修單元集合，且|J|=m，m為維修單元的總數。

4)C為裝備重要度的集合，C={c1，c2，…，cn}，c1，c2，…，cn表示各待修裝備的重要度。

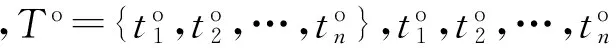
7)T為完成維修任務所需時間的集合，T={t1，t2，…，tn}，t1,t2,…,tn表示修復各待修裝備所需的時間。

10)xij為分配變量，xij=1表示將第i維修任務分配給第j個裝備維修單元，xij=0表示沒有將第i維修任務分配給第j個裝備維修單元。

2.2 維修任務分配模型

以非平衡指派模型為基礎，結合裝備維修任務分配特點，可以得到裝備維修任務分配模型為

(1)

(2)

(3)

(4)

(5)

xij={0,1}.

(6)

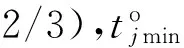
2.3 模型求解

2.3.1 兩階段啟發式算法

兩階段啟發式算法[13]，是根據需要將問題劃分為兩個階段性問題，根據各階段問題的特點應用不同的啟發式算法求解問題的過程。

根據維修任務分配的最終結果，將維修任務分配分解為任務劃分和順序確定兩個階段。第一階段是通過任務劃分，明確維修任務與裝備維修單元之間的對應關系，應用遺傳算法求解；第二階段是明確各裝備維修單元完成維修任務的先后順序，由于此階段可行解較少，為確保搜索的完整性，應用鄰域搜索算法[14]進行求解。

2.3.2 算法設計

1)第一階段——遺傳算法

①編碼方式：采用整數編碼，染色體長度為n，對應維修任務的數量。每個基因在0～m中取整數值，0表示該任務沒有被分配，1～m表示任務分配給對于標號的裝備維修單元。

②種群初始化：通過隨機數產生初始種群，初始種群中每個染色體上的編碼都在0～m之間隨機取正整數。

③交叉與變異：交叉采用單切點交叉法，通過正比例選擇策略選擇父代染色體。變異采用交換變異，即選擇染色體中的若干個基因交換位置。

2)第二階段——鄰域搜索

①編碼方式：采用整數編碼，對每個維修單元所分配任務按照編號從小到大的順序進行編碼。

②搜索方法：采用隨機變化法實現鄰域交換。

③搜索次數：由于每個維修單元所分配任務的數量存在差異，搜索次數會隨著維修任務數量增加呈幾何倍數增長。設維修單元所示分配維修任務量為Q，設置一個上限值M，搜索次數設定為min (M,Q!).

3)適應度函數

適應度函數為維修任務分配模型的目標函數。

4)編碼轉化

兩階段涉及的編碼不同，需要進行轉換，設計如下的轉化方式：

①對任意染色體CH，在鄰域搜索前用S1～Sm共m個向量提取染色體上m個裝備維修單元各自對應的維修任務，然后對S1～Sm分別進行鄰域搜索，進行時間約束和維修能力約束的判斷，并獲得符合條件的最優執行順序，同時計算對應的裝備重要度之和C′1～C′m.

②用向量S作為染色體CH的輸出向量獲取最優執行順序，不同裝備維修單元對應的執行順序用數字0隔開，即

(7)

這樣就可以建立CH與S的一一對應關系，易得S的最大長度為n+m-1. 同時對C′1～C′m進行求和，獲得該染色體對應的適應度值C′max.

5)約束條件判斷

獲得備選方案后，首先對約束條件進行判斷，若不符合約束條件，則該方案不是可行解，無需進行后續運算步驟。

①時間約束判斷：結合(4)式、(5)式、(6)式對時間約束進行判斷。

②維修能力約束判斷：由于維修能力約束具有實時性，需要在每次隨性維修任務前進行判斷。若裝備維修單元j的備選方案為(j1,j2,…,jq)(1≤q≤n)，即按照j1,j2,…,jq順序遂行維修任務，則必須滿足對?λ，均有

(8)

則備選方案符合維修能力約束條件。

6)運算步驟

運用兩階段啟發式算法求解模型的步驟為：

步驟1 給定初始參數：種群規模K、遺傳算法最大迭代次數L、交叉概率Pc、變異概率Pm，鄰域搜索上限M.

步驟2 隨機產生規模為K的初始種群U0，初始化遺傳算法迭代次數l=0.

步驟3 判斷截止條件，若l≤L，轉到步驟4，否則，轉到步驟11.

步驟5 對初始編碼進行鄰域搜索，產生新鄰域后進行時間約束和維修能力約束判斷，不符合條件的適應度值設為0，符合條件的計算出適應度值。

步驟6 將各染色體最優結果所對應的適應度值作其適應度值，更新此維修任務最優分配結果。

步驟7 從種群Ul中依據正比例選擇策略選擇父代個體。

步驟8 取ζ∈[0,1]的隨機數，若ζ>Pc則將父代個體保留，否則將按照單切點交叉算子得到子代個體，轉到步驟9.

步驟9 取ζ∈[0,1]的隨機數，若ζ>Pm則個體不發生變異，否則按照變異算子對個體進行變異，得到子代種群，轉到步驟10.

步驟10 計算子代染色體的適應值，將子代種群與父代種群合并，用子代個體代替父代中適應值小的個體，計算各個染色體的適應值并按從大到小排序；令l=l+1，保留前K個染色體作為新的種群Ul，返回步驟3.

步驟11 運算終止，輸出最優解(包括最優分配結果bestnote和對應的裝備重要度之和Cmax)。

3 算例分析

3.1 算例背景

為了驗證維修任務分配模型，構建了以下算例：某團執行機動進攻作戰任務，該團共有100臺裝甲裝備和15臺自行火炮裝備等主戰裝備。經過一段時間后，由于故障和敵方火力打擊，裝備陸續出現損壞，通過信息偵察，屬于本級維修任務的共有18個(編號為1～18)，該團派出3個裝備維修單元(編號為1、2、3)遂行裝備維修任務。

表1 維修任務基本信息

裝備維修任務相互距離信息，即裝備維修單元在各裝備維修任務之間的機動時間，如表2所示。

維修任務約束條件信息，包括各裝備維修單元的初始維修能力(所能承擔的初始最大工作時間)信息和作戰時間信息，如表3所示。

3.2 維修任務分配結果

根據維修任務分配模型，將算例中的基本信息作為輸入條件，通過設計的算法(取K=20，L=50，Pc=0.85，Pm=0.01，M=2 000)，利用MATLAB軟件運算，得出迭代結果如圖1所示。

計算結果為

表2 維修任務相互距離信息

表3 維修任務約束條件信息

圖1 遺傳算法迭代結果Fig.1 Iteration result of genetic algorithm

(9)

Cmax=5.697.

(10)

即維修任務分配結果如表4所示。

表4 維修任務分配結果

3.3 結果分析

本文主要考慮了維修任務的時間限制和維修能力限制兩大約束條件，并且以完成維修任務的裝備重要度之和最大為決策目標，在同樣的背景下分別釋放約束條件，計算最優分配結果如表5所示。

通過表4與表5對比，可得：

1)在不考慮維修能力限制的條件下(表5條件1)，所對應的Cmax為5.915高于表4中的Cmax為5.697，但是分配裝備維修單元2的維修任務工作量為165 min，大于其實際維修能力，不符合實際情況，屬于無效解。

2)在不考慮時間限制的條件下(表5條件2)，裝備維修單元可以完成所有的維修任務，所對應的Cmax也最大。但是，分配給裝備維修單元2的維修任務1、維修任務3和分配給裝備維修單元3的維修任務17、維修任務18，均是在作戰時間的后1/3完成的，不能對作戰起支持作用，屬于無效修復。而去除無效修復以后，條件2所對應的Cmax下降為5.072，小于表4中的Cmax為5.697.

表5 維修任務分配結果對比

3)在不考慮裝備重要度時(表5條件3)，所對應的Cmax為5.119小于表4中的Cmax為5.697.

通過以上分析，可以發現本文所述方法可以獲得滿足約束條件的最優可行解，可以有效地解決多約束條件下的戰時維修任務分配問題。

4 結論

1)維修能力限制是戰時裝備維修任務分配的重要約束條件，忽略這個條件會出現不可行解，使得裝備維修單元可能無法完成所分配的全部維修任務，從而影響裝備維修系統效能的充分發揮。

2)時間限制是戰時裝備維修任務分配的重要約束條件，忽略這個條件可能會出現無效修復，不能充分發揮裝備維修對作戰的支持作用。

3)將裝備重要度作為維修任務分配目標的重要影響因素，以修復裝備重要度之和最大作為決策目標，更加能夠發揮戰時裝備維修系統保證裝備體系完整的作用。

戰時裝備維修任務分配需要滿足必要的約束條件，才能使維修任務分配更加合理有效，更好地為體系作戰服務。

References)

[1] Jia Y X, Sun L, Wang Y B, et al. Research on maintenance task allocation and support resource requirement analysis for ordnance equipment[C]∥2012 International Conference on Quality, Reliability, Risk, Maintenance and Safety Engineering. Chendu, Sichuan, China: IEEE, 2012:459-465.

[2] Chen H G. The dynamic allocation model of equipment maintenance task based on comprehensive balance[C]∥2010 3rd International Conference on Information Management, Innovation Management and Industrial Engineering. Kunming, Yunnan, China: IEEE, 2010,11:3-9-323.

[3] 凌海風,周獻中,江勛林,等.基于多目標粒子群優化算法的裝備維修任務分配[J].計算機應用研究, 2012,29(6):2090-2092. LING Hai-feng, ZHOU Xian-zhong, JIANG Xun-lin, et al. Study on equipment maintenance task assignment based on multi-objectives particle swarm optimization[J]. Application Research of Computers, 2012,29(6):2090-2092. (in Chinese)

[4] Yuan C, Guo L B, Yong Q D. Research on the maintenance task allocation of oil equipment[C]∥2012 IEEE Symposium on Robotics and Applications. Kuala Lumpur, Malaysia: IEEE, 2012:97-100.

[5] 陳冰,朱小冬,王毅剛,等.裝備完好率要求和人才成長規律的維修任務分配方法[J].火力與指揮控制,2014,39(9):96-99. CHEN Bing， ZHU Xiao-dong， WANG Yi-gang, et al. Research on materiel readiness rate and talented person growing law of task allocation model[J]. Fire Control & Command Control,2014,39(9):96-99. (in Chinese)

[6] 申卯興,曹澤陽,周林.現代軍事運籌[M].北京:國防工業出版社,2015. SHEN Mao-xing, CAO Ze-yang, ZHOU Lin. Modern military operations research[M].Beijing: Natonal Defense Industry Press, 2015. (in Chinese)

[7] Zhang Y, Yang R N, Zuo J L, et al. Improved MOEA/D for dynamic weapon-target assignment problem[J]. Journal of Harbin Institute of Technology,2015,22(6):121-128.

[8] Gottlieb Y, Shima T. UAVs task and motion planning in the presence of obstacles and prioritized targets[J]. Sensors, 2015,15(11):29734-29764.

[9] Lampang A, Boonjing V, Chanvarasuth P. A cost and space efficient method for unbalanced assignment problems[C]∥2010 IEEE International Conference on Industrial Engineering and Engineering Management. Macao: IEEE, 2010:985-988.

[10] Jammoussi Y A, Ghribi F S, Masmoudi S D. Genetic algorithms-based dominant feature selection for face detection application[J]. International Journal of Computational Vision and Robotics,2016,6(1): 77-93.

[11] Eftekhari M, Eftekhari M. Controller design for multivariable nonlinear control systems based on gradient-based ant colony optimisation[J]. International Journal of Modelling, Identification and Control, 2016,25(1): 38-47.

[12] Gu F Q, Liu H L, Li X Q. A fast evolutionary algorithm with searching preference[J]. International Journal of Computational Science and Engineering,2016,12(1): 29-37.

[13] Guemri O, Beldjilali B. Two-stage heuristic algorithm for the large-scale capacitated location routing problem[J]. Journal of Guidance Control and Dynamics,2016,39(9): 1934-1948.

[14] Wang P, Reinelt G, Tan Y J. Self-adaptive large neighborhood search algorithm for parallel machine scheduling problems[J]. Journal of Systems Engineering and Electronics,2012,23(2):208-215.

Task Allocation Method for Wartime Equipment Maintenance under Multiple Constraint Conditions

ZAN Xiang, CHEN Chun-liang, ZHANG Shi-xin, WANG Zheng, LIU Yan

(Department of Technical Support Engineering, Academy of Armored Force Engineering, Beijing 100072, China)

A model of equipment maintenance task allocation is established for lack of constraint conditions of existing wartime equipment maintenance task allocation. The model can be used for optimal decision of maintenance task allocation in the case of time constraint and maintainability limitation. And the equipment repair time, maneuver time and maintainability are comprehensively considered in the model. A two-stage heuristic algorithm, including genetic algorithm and neighborhood searching method, is designed to solve the model. The effectiveness of the proposed algorithm is verified through example analysis and comparison.

ordnance science and technology;equipment maintenance task allocation; multiple constraint; assignment problem; two-stage heuristic algorithm

2017-01-16

軍隊科研計劃項目(2015WG57)

昝翔(1989—)，男，博士研究生。E-mail：994401550@qq.com

陳春良(1963—)，男，教授，博士生導師。E-mail：chenchunliang@163.com

E92

A

1000-1093(2017)08-1603-07

10.3969/j.issn.1000-1093.2017.08.019