雙重優(yōu)化的寬帶聚焦波束形成算法研究

畢楊, 王英民, 王奇

(1.西安航空學(xué)院 電子工程學(xué)院, 陜西 西安 710077; 2.西北工業(yè)大學(xué) 航海學(xué)院，陜西 西安 710072)

雙重優(yōu)化的寬帶聚焦波束形成算法研究

畢楊1,2, 王英民2, 王奇2

(1.西安航空學(xué)院 電子工程學(xué)院, 陜西 西安 710077; 2.西北工業(yè)大學(xué) 航海學(xué)院，陜西 西安 710072)

在相干信號(hào)子空間法中確定聚焦矩陣時(shí)，對(duì)初始方向估計(jì)的偏差和聚焦頻率選擇的偏差都會(huì)影響最終的聚焦效果，甚至?xí)顾惴ㄊАａ槍?duì)這個(gè)缺陷，提出了一種雙重優(yōu)化的寬帶聚焦波束形成算法。該算法利用穩(wěn)健Capon波束形成算法對(duì)聚焦矩陣進(jìn)行修正，使寬帶信號(hào)通過(guò)修正的聚焦矩陣全部聚焦在最佳聚焦頻率上，再對(duì)窄帶數(shù)據(jù)利用2階錐方法實(shí)現(xiàn)波束形成。計(jì)算機(jī)仿真以及湖試實(shí)驗(yàn)結(jié)果表明，該算法在保證波束恒定的前提下，在各個(gè)頻率點(diǎn)都具有更低的旁瓣級(jí)。

聲學(xué)； 最佳聚焦矩陣； 最佳聚焦頻率； RCB算法； 2階錐規(guī)劃； 寬帶波束形成

0 引言

波束形成可以使陣列信號(hào)形成基陣接收系統(tǒng)的方向性，提高信噪比；通過(guò)空域?yàn)V波，抑制空間干擾；進(jìn)行多目標(biāo)分辨，實(shí)現(xiàn)目標(biāo)方位估計(jì)；在目標(biāo)定位、距離、深度估計(jì)方面有很大的作用；還為目標(biāo)識(shí)別提供信息[1]。窄帶信號(hào)中包含的關(guān)于目標(biāo)信息有限，因此選用寬帶信號(hào)進(jìn)行參量估計(jì)、目標(biāo)檢測(cè)和特征提取。寬帶信號(hào)的波束形成算法研究非常有意義。對(duì)于寬帶信號(hào)的波束形成處理，通常有兩種方法：非相干信號(hào)子空間法(ISM)，和相干信號(hào)子空間法(CSM)。在CSM中，通過(guò)聚焦矩陣使寬帶信號(hào)劃分的不同頻率的窄帶信號(hào)都映射到同一個(gè)參考頻率上，再利用窄帶波束形成算法實(shí)現(xiàn)寬帶聚集波束形成[2-3]。與ISM相比，CSM中的聚焦操作充分地綜合了寬帶信息，使聚焦后的信號(hào)協(xié)方差矩陣保持滿秩，因此，寬帶波束形成的問(wèn)題得到有效解決。該算法運(yùn)算量小、估計(jì)精度高，能夠有效地克服信號(hào)抵消、擴(kuò)展檢測(cè)及分辨門限，能夠處理多途環(huán)境問(wèn)題等[4-6]。聚焦矩陣的構(gòu)造是CSM的核心，聚焦矩陣的構(gòu)造方法對(duì)CSM的估計(jì)性能起著決定性作用。確定聚焦矩陣時(shí)，有兩個(gè)因素決定最終的聚焦效果。一個(gè)是對(duì)初始方向的估計(jì)，另一個(gè)是選擇的聚焦頻率。對(duì)初始方向估計(jì)的偏差和聚焦頻率選擇的偏差都會(huì)影響最終的聚焦效果，甚至?xí)顾惴ㄊА?duì)于這個(gè)缺陷，文獻(xiàn)[7]中利用穩(wěn)健Capon波束形成(RCB)算法對(duì)聚焦矩陣進(jìn)行校正，改善了預(yù)估計(jì)偏差對(duì)聚焦效果的影響，但尚未考慮聚焦頻率對(duì)聚焦效果的影響[7-9]。文獻(xiàn)[10]中利用2階錐規(guī)劃方法來(lái)補(bǔ)償聚焦矩陣的誤差，而在該算法中也沒(méi)有考慮到最佳聚焦頻率的確定問(wèn)題。本文考慮到了最佳聚焦頻率的確定問(wèn)題，將RCB算法的優(yōu)點(diǎn)和2階錐規(guī)劃方法的優(yōu)點(diǎn)結(jié)合在一起，提出了一種雙重優(yōu)化的寬帶聚焦波束形成算法。該算法與文獻(xiàn)[7，10]相比，其波束形成效果更優(yōu)。

1 信號(hào)模型

設(shè)s(t)為入射信號(hào)，第m個(gè)陣元接收到的寬帶信號(hào)為

xm(t)=s(t-τm)+nm(t),
m=1,2,…,M,

(1)

式中：τm為第m個(gè)陣元處接收的信號(hào)相對(duì)于s(t)的時(shí)延；nm(t)為第m個(gè)陣元疊加的加性噪聲。把每個(gè)陣元的輸出分成K個(gè)不重疊的數(shù)據(jù)塊，每塊含有L個(gè)采樣點(diǎn)。然后對(duì)每塊數(shù)據(jù)進(jìn)行L點(diǎn)的快速傅里葉變換，就可以得到L個(gè)頻率子帶上的數(shù)據(jù)，每個(gè)頻率子帶上含有K個(gè)數(shù)據(jù)快拍。第l個(gè)頻率子帶上的頻域數(shù)據(jù)用矩陣形式表示為

Xk(fl)=Al(φ,θ)s(fl)+nk(fl),
k=1,…,K,l=1,…,L,

(2)

式中：fl表示第l個(gè)頻率子帶；Al(φ,θ)表示信號(hào)第l個(gè)頻率子帶上對(duì)應(yīng)方向(φ,θ)的導(dǎo)向矢量，φ是俯仰角，θ是方位角。二維空間的波束形成是三維空間波束形成的特例，具有代表性，本文僅在二維平面內(nèi)進(jìn)行寬帶聚焦波束形成，相應(yīng)的Al(φ,θ)簡(jiǎn)寫為A(fl,θ).

2 寬帶聚焦波束形成算法

聚焦變換過(guò)程中聚焦矩陣應(yīng)使(3)式[10]成立：

T(fj)A(fj,θ)=A(f0,θ),j=1,2,…，J,

(3)

式中：fj為寬帶范圍內(nèi)任意窄帶頻率；f0為聚焦頻率；A(fj,θ)為第j個(gè)頻率子帶上的導(dǎo)向矢量；T(fj)為聚焦矩陣。

本文中聚焦矩陣T(fj)選擇文獻(xiàn)[11]中提到的旋轉(zhuǎn)信號(hào)子空間(RSS)法。

最佳聚焦矩陣可按(4)式[10]確定：

(4)

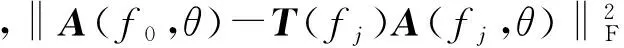
2.1 最佳聚焦頻率的確定

由(4)式可知，由(5)式可確定擬合誤差[11]為

(5)

對(duì)于任意陣列，其方向矩陣A(fj,θ)滿足：

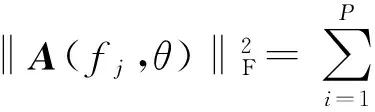
(6)

式中：i指信號(hào)的個(gè)數(shù)，i=1,2,…,P. 將(6)式代入(5)式，可得

(7)

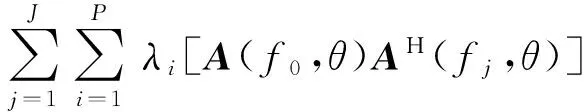
(8)

當(dāng)F取最大值時(shí)，聚焦擬合誤差可取最小值。對(duì)于各種陣列的方向矩陣，只要信號(hào)的個(gè)數(shù)P小于陣元個(gè)數(shù)M，(9)式均成立：

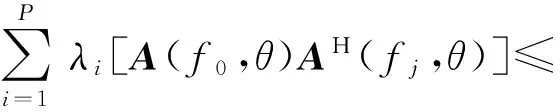
(9)

令

(10)

則

(11)

通過(guò)(11)式可確定最佳聚焦頻率f0，其算法的時(shí)間復(fù)雜度為O(n3)。

2.2 雙重優(yōu)化的寬帶聚焦波束形成算法原理

頻域樣本值估計(jì)出的相關(guān)矩陣為

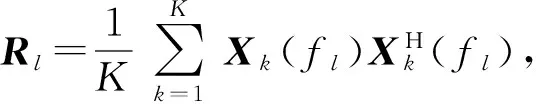
(12)

式中：K指每個(gè)頻率子帶上含有的數(shù)據(jù)快拍個(gè)數(shù)。根據(jù)給定的寬帶信號(hào)的頻率范圍，按照2.1節(jié)中最佳聚焦頻率的確定方法確定出最佳的聚焦頻率f0，基于RCB算法的波束形成就變成

(13)

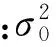
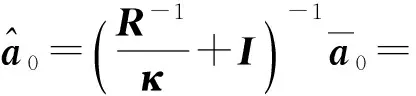
(14)

式中:κ由牛頓迭代法確定[12-13]；R為協(xié)方差矩陣。同理可以得到其他參考頻率fl上的校正導(dǎo)向矢量l. 用矯正過(guò)的0和l可以確定矯正的聚焦矩陣為

l(φ,θ)=(fl)H(fl).

(15)

通過(guò)聚焦矩陣預(yù)處理后各子帶的數(shù)據(jù)都聚焦在最佳聚焦頻率f0上。

第l個(gè)頻率子帶上的聚焦數(shù)據(jù)[14]為

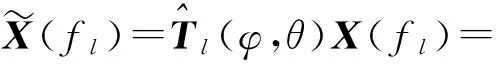
(16)

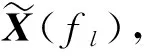
穩(wěn)健的低旁瓣窄帶波束形成可以保證波束對(duì)觀察方向的響應(yīng)為1的條件下，使得旁瓣級(jí)最小,同時(shí)考慮波束形成的穩(wěn)健性，對(duì)波束形成的加權(quán)向量進(jìn)行約束。即

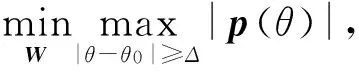
(17)

式中：θ0為觀察方向；Δ的取值是在波束主瓣的左右兩側(cè)與最高旁瓣相等的兩角度寬度的二分之一；p(θ)為波束對(duì)觀察方向的響應(yīng)；W為波束形成的加權(quán)向量；σ為權(quán)向量范數(shù)的約束上限。引入非負(fù)實(shí)變量y1，令θs(s=1,2,…,S)表示旁瓣部分離散化的S個(gè)方向，(17)式可寫成

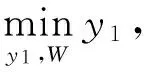
(18)

給定Δ值，通過(guò)上式可求出y，即非負(fù)實(shí)變量y1的最小值，得到優(yōu)化波束加權(quán)向量W.

各個(gè)子帶的加權(quán)向量Wl都滿足：

Wl=W0，

(19)

則f0和fl頻率上的基陣輸出波束圖p0(φ,θ)與pl(φ,θ)分別為

(20)

(21)

使得p0(φ,θ)=pl(φ,θ)，即

(22)

可以實(shí)現(xiàn)各窄帶波束形成的波束寬度都恒定。

3 仿真實(shí)驗(yàn)與性能分析

假定入射信號(hào)是頻率范圍為[750 Hz，1 500 Hz]的寬帶信號(hào)，該寬帶信號(hào)帶寬為750 Hz，中心頻率為1 125 Hz. 仿真陣列由24個(gè)各向同性陣元組成的均勻分布圓形陣，其半徑為0.5 m，對(duì)陣元接收的寬帶信號(hào)利用寬帶聚焦的波束形成算法，在0°方向?qū)崿F(xiàn)寬帶信號(hào)波束形成。

3.1 仿真1：最佳聚焦頻率有效性的驗(yàn)證

為了能夠體現(xiàn)最佳聚焦頻率在寬帶聚焦波束形成中的有效性，在這里進(jìn)行了5組仿真實(shí)驗(yàn)，將寬帶信號(hào)劃分為21個(gè)窄帶信號(hào)，通過(guò)RSS算法使21個(gè)子帶信號(hào)分別聚焦在750 Hz、850 Hz、1 350 Hz、1 500 Hz以及最佳聚焦頻率879 Hz上，再利用常規(guī)波束形成算法。得到了在不同聚焦頻率上的波束圖，分別如圖1～圖5所示。圖1(a)是879 Hz的窄帶信號(hào)的常規(guī)波束形成圖，圖1(b)是頻率范圍[750 Hz，1 500 Hz]的寬帶信號(hào)通過(guò)RSS算法聚焦在最佳聚焦頻率879 Hz的寬帶聚焦波束疊加圖。圖2～圖5分別是聚焦頻率為750 Hz、850 Hz、1 350 Hz和1 500 Hz的仿真實(shí)驗(yàn)結(jié)果。

圖1 最佳聚焦頻率879 Hz上的仿真實(shí)驗(yàn)對(duì)比圖Fig.1 Experimental comparison of the optimal focusing frequencies at 879 Hz

圖2 聚焦頻率在750 Hz上的仿真實(shí)驗(yàn)對(duì)比圖Fig.2 Experimental comparison of focusing frequencies at 750 Hz

圖3 聚焦頻率在850 Hz上的仿真實(shí)驗(yàn)對(duì)比圖Fig.3 Experimental comparison of focusing frequencies at 850 Hz

圖4 聚焦頻率在1 350 Hz上的仿真實(shí)驗(yàn)對(duì)比圖Fig.4 Experimental comparison of focusing frequencies at 1 350 Hz

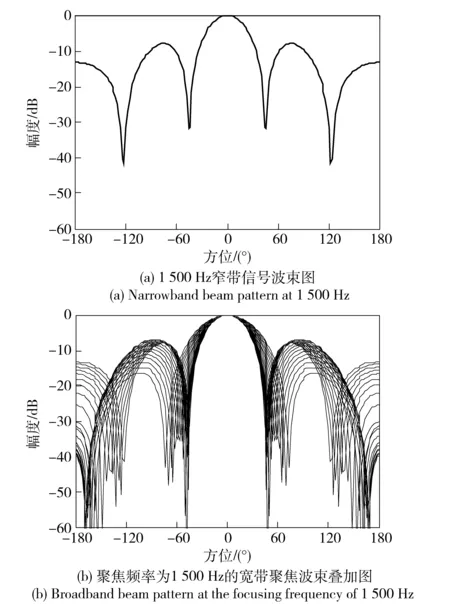
圖5 聚焦頻率在1 500 Hz上的仿真實(shí)驗(yàn)對(duì)比圖Fig.5 Experimental comparison of focusing frequencies at 1 500 Hz

從波束圖的主瓣寬度、旁瓣級(jí)的角度對(duì)5種聚焦頻率下寬帶波束形成的效果進(jìn)行了對(duì)比分析。從以上的對(duì)比結(jié)果及表1、表2、表3的數(shù)據(jù)分析可以看出，在最佳聚焦頻率聚焦的寬帶波束與其對(duì)應(yīng)的窄帶波束的一致性較好，圖1(b)中各個(gè)頻率上的主瓣寬度與其對(duì)應(yīng)的窄帶波束相差5.73°，旁瓣級(jí)接近圖1(a)中的窄帶信號(hào)旁瓣級(jí)，只相差0.75 dB. 在確定聚焦頻率點(diǎn)時(shí)，當(dāng)選擇的聚焦頻率小于879 Hz的仿真結(jié)果如圖2和圖3所示，聚焦前后的寬帶波束與窄帶波束的一致性較差，寬帶聚焦波束的主瓣寬度可以保持較好的一致性，主瓣寬度變化較小，但是旁瓣級(jí)變化較大，達(dá)到了3.83 dB. 當(dāng)選擇的聚焦頻率大于879 Hz的仿真結(jié)果如圖4和圖5所示，聚焦前后的寬帶波束與窄帶波束的一致性較差，寬帶聚焦波束的主瓣寬度也可以保持較好的一致性，但是主瓣寬度變化較大，達(dá)到了19.72°，旁瓣級(jí)變化也較大。因此，通過(guò)聚焦變換在最佳聚焦頻率上的寬帶聚焦波束圖的效果是最優(yōu)的。從而證明了最佳聚焦頻率的有效性。

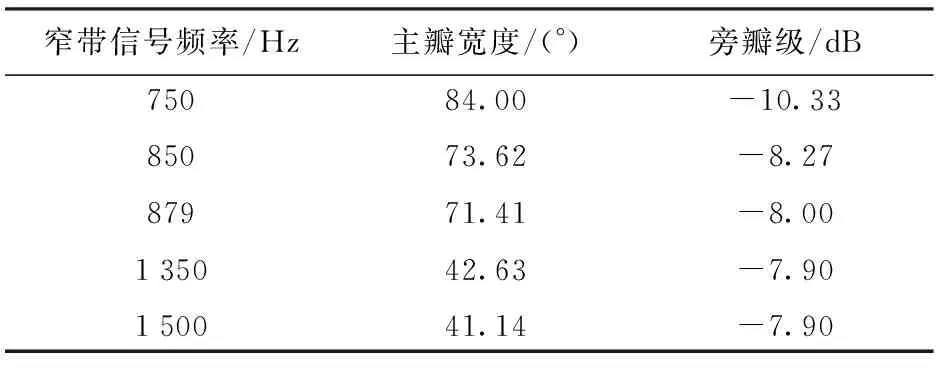
表1 窄帶信號(hào)波束形成參數(shù)對(duì)比

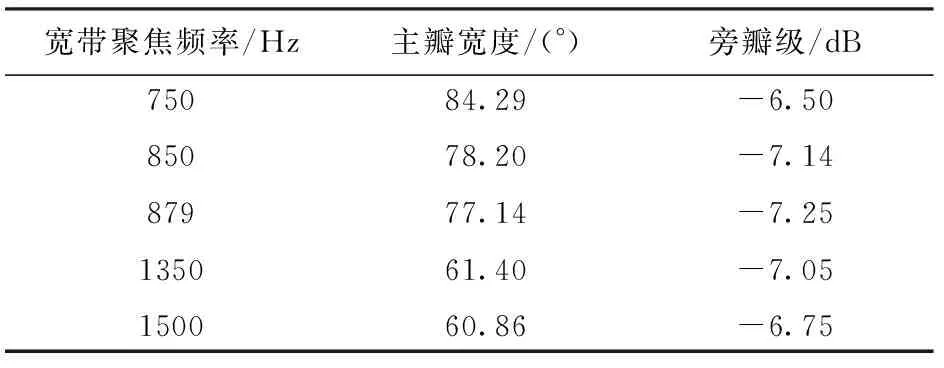
表2 寬帶信號(hào)波束形成參數(shù)對(duì)比

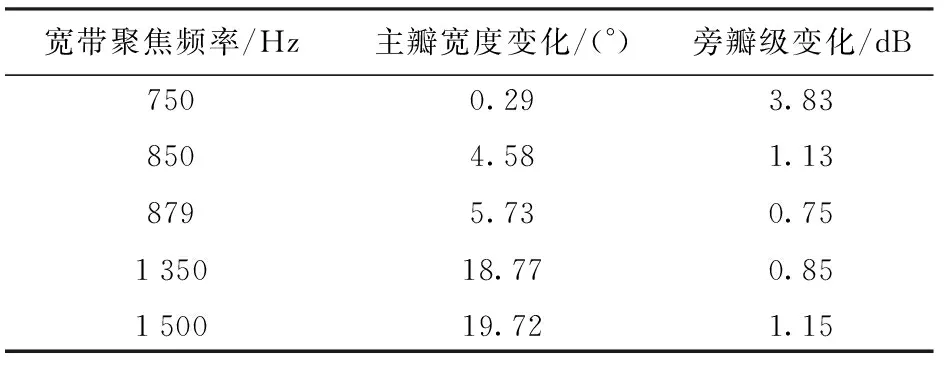
表3 窄帶信號(hào)與寬帶信號(hào)波束形成參數(shù)變化對(duì)比

3.2 仿真2：基于RCB優(yōu)化的寬帶聚焦波束形成算法

為了驗(yàn)證RCB算法對(duì)聚焦矩陣的修正作用，使21個(gè)窄帶信號(hào)利用RCB算法校正的最佳聚焦矩陣(fj)聚焦在最佳聚焦頻率f0=879 Hz上，將寬帶問(wèn)題轉(zhuǎn)換為窄帶問(wèn)題后，利用常規(guī)波束形成算法完成寬帶聚焦波束形成。該算法的時(shí)間復(fù)雜度為O(n3)。

由圖6可以看出，該算法得到的寬帶聚焦波束其主瓣為76.43°，旁瓣級(jí)為7.4 dB，與圖1(b)中未通過(guò)RCB校正的寬帶聚焦波束對(duì)比，可以看出其波束形成效果優(yōu)于校正前的波束圖，其寬帶波束與其對(duì)應(yīng)的窄帶波束保持了較好的一致性，主瓣寬度減小了0.71°，旁瓣級(jí)下降了0.15 dB. 從而證明了RCB算法在寬帶聚焦波束形成中有效地修正了聚焦矩陣。

圖6 RCB校正后聚焦在879 Hz寬帶波束圖Fig.6 Broadband beam pattern at 879 Hz after RCB correction

3.3 仿真3：基于最佳聚焦頻率的2階錐寬帶聚焦波束形成算法

將寬帶信號(hào)劃分為21個(gè)窄帶信號(hào)，設(shè)每個(gè)窄帶的中心頻率為fj，j=1,2，…,21. 利用最佳聚焦頻率的確定方法確定出該寬帶信號(hào)的最佳聚焦頻率為f0=879 Hz；利用RSS聚焦算法使j個(gè)窄帶信號(hào)全部聚焦在最佳聚焦頻率f0=879 Hz上；最后利用2階錐規(guī)劃方法完成窄帶波束形成。該算法的時(shí)間復(fù)雜度為O(n2)。

由圖7可以看出，該算法得到的波束疊加圖，其主瓣寬度為26.6°，旁瓣級(jí)可以達(dá)到23.3 dB，與常規(guī)波束形成算法相比較有更好的波束形成效果。

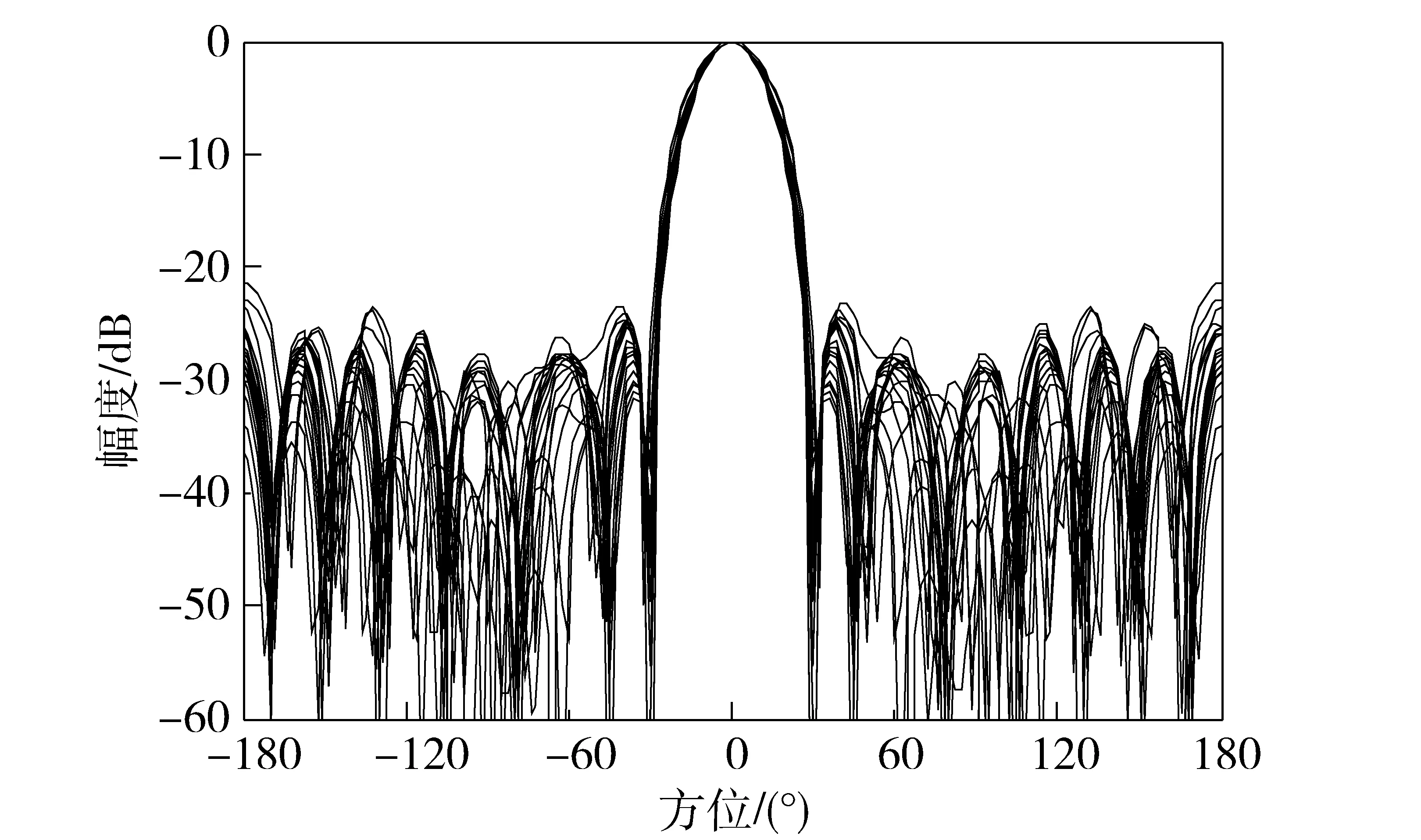
圖7 基于最佳聚焦頻率的2階錐寬帶聚焦波束圖Fig.7 Two-order cone broadband focusing beam pattern based on optimal focusing frequency

3.4 仿真4：雙重優(yōu)化的寬帶聚焦波束形成算法

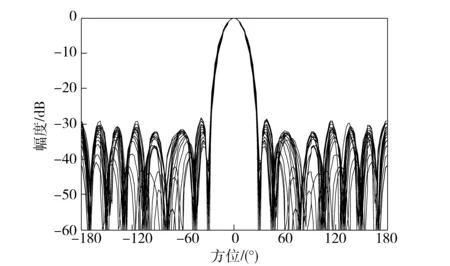
圖8 雙重優(yōu)化的寬帶聚焦波束圖Fig.8 Dual optimized broadband focusing beam pattern

寬帶信號(hào)通過(guò)雙重優(yōu)化的寬帶聚焦波束形成，其寬帶波束主瓣保持恒定，主瓣寬度為22.8°，旁瓣級(jí)可以達(dá)到28.5 dB. 與之前的波束圖對(duì)比，通過(guò)雙重優(yōu)化的寬帶聚焦波束形成，其波束形成的效果是最優(yōu)的。為了進(jìn)一步驗(yàn)證算法的有效性，對(duì)該算法進(jìn)行了湖試實(shí)驗(yàn)驗(yàn)證。

4 湖試實(shí)驗(yàn)

本文中的算法在某水庫(kù)進(jìn)行了湖試實(shí)驗(yàn)驗(yàn)證。實(shí)驗(yàn)水域深為8.5 m，水面較為開闊，采用24元圓環(huán)形基陣，半徑為0.5 m. 發(fā)射信號(hào)由美國(guó)HP/Agilent公司產(chǎn)HP33120A函數(shù)/任意波形發(fā)生器產(chǎn)生，頻率范圍[750 Hz，1 500 Hz]，為矩形調(diào)制的正弦脈沖信號(hào)，選用其中8個(gè)頻率點(diǎn)，分別為750 Hz、857 Hz、964 Hz、1 071 Hz、1 178 Hz、1 285 Hz、1 392 Hz、1 500 Hz.發(fā)射信號(hào)通過(guò)增益為50 dB功放放大后送到鑲拼圓環(huán)發(fā)射換能器作為聲源。發(fā)射過(guò)程中濾波放大器的輸入、輸出增益保持不變，但濾波的中心頻率和信號(hào)頻率保持一致。數(shù)據(jù)采集系統(tǒng)的采樣頻率為50 kHz，數(shù)據(jù)存儲(chǔ)長(zhǎng)度設(shè)為5 s，平均輸入信噪比約為37 dB.

先利用RCB算法對(duì)實(shí)測(cè)的8組陣列流形進(jìn)行校正，由校正的陣列流形確定出修正的聚焦矩陣，在[750 Hz，1 500 Hz]的頻率范圍內(nèi)，由最佳聚焦頻率的確定方法確定出最佳聚焦頻率f0=879 Hz，權(quán)值是通過(guò)24陣元的理想圓陣的陣列流形設(shè)計(jì)得到的，是基于最佳聚焦頻率的2階錐的寬帶聚焦波束形成算法的權(quán)值，得到如圖9所示，并與基于最佳聚焦頻率的常規(guī)寬帶聚焦波束形成算法，以及2階錐寬帶波束形成算法進(jìn)行對(duì)比，如圖10所示。

圖9 實(shí)測(cè)流型的8頻率點(diǎn)波束疊加圖Fig.9 Beam superposition of measured array manifolds at 8 frequency points

由圖9、圖10及表4可以看出：寬帶信號(hào)在8個(gè)頻率點(diǎn)的主瓣寬度都可以保持較好的一致性，其寬度差不超過(guò)2.5°；在8個(gè)頻率點(diǎn)中，最高的旁瓣級(jí)為21.0 dB，最低的旁瓣級(jí)為33.0 dB. 通過(guò)圖10中本文算法分別與常規(guī)波束形成算法和2階錐寬帶波束形成算法的對(duì)比，可以看出本文提出的雙重優(yōu)化算法在保證波束恒定的前提下，在各個(gè)頻率點(diǎn)都具有更低的旁瓣級(jí)，從而證明了該算法的有效性。

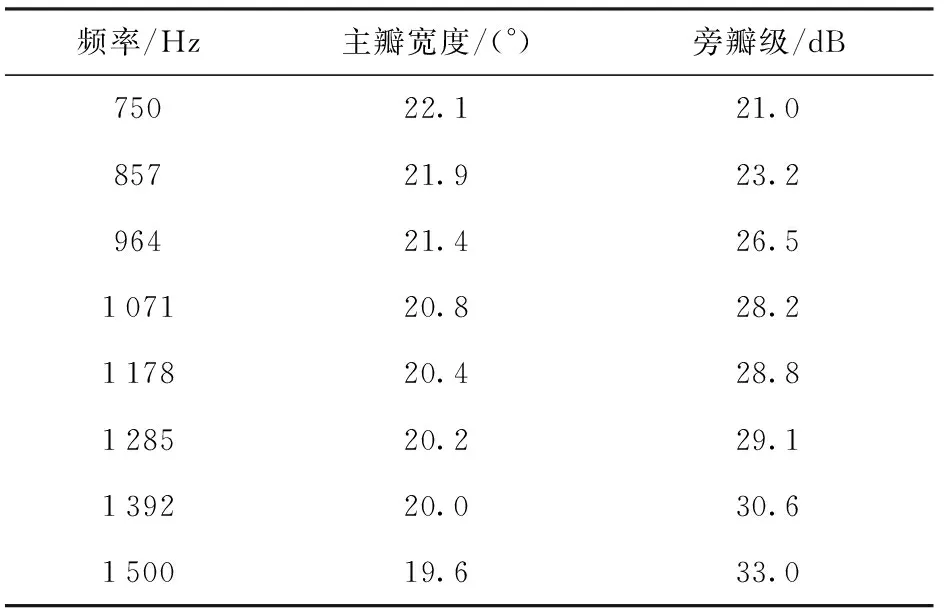
表4 寬帶信號(hào)8頻率點(diǎn)的波束參數(shù)

5 結(jié)論

本文研究了利用CSM算法解決寬帶聚焦波束形成問(wèn)題，提出了雙重優(yōu)化的寬帶聚焦波束形成算法。該算法利用RCB算法修正聚焦矩陣，使寬帶信號(hào)聚焦在此頻帶范圍的最佳聚焦頻率上，再利用基于2階錐的最低旁瓣波束形成算法。這不僅彌補(bǔ)了在確定聚焦矩陣時(shí)，對(duì)初始方向估計(jì)的偏差對(duì)聚焦效果的影響，還考慮到聚焦頻率選擇的偏差對(duì)聚焦效果的影響。通過(guò)仿真實(shí)驗(yàn)和湖試實(shí)驗(yàn)的驗(yàn)證，證明了最佳聚焦頻率的有效性，以及RCB算法在寬帶聚焦波束形成中對(duì)聚焦矩陣的修正作用，從而進(jìn)一步表明雙重優(yōu)化的寬帶聚焦波束形成算法在保證波束恒定的前提下，在不同的頻率點(diǎn)處的旁瓣級(jí)更低，波束形成效果更優(yōu)，從而驗(yàn)證了該算法的有效性。

References)

[1] 陳輝, 趙擁軍, 劉成城,等.基于二次型約束的穩(wěn)健寬帶恒定束寬波束形成[J].數(shù)據(jù)采集與處理, 2016, 31(4):815-822. CHEN Hui, ZHAO Yong-jun, LIU Cheng-cheng, et al.Robust wideband constant beamwidth beamforming algorithm based on quadratic constraint[J].Journal of Data Acquisition and Processing, 2016, 31(4):815-822.(in Chinese)

[2] Hung H S,Mao C Y.Robust coherent signal-subspace processing for direction of arrival estimation of wideband sources[J]. IEEE Proceedings of Radar,Sonar and Navigation, 1994, 141(5): 256-262.

圖10 實(shí)測(cè)流型的8頻率點(diǎn)波束圖Fig.10 Beam patterns of measured array manifolds at 8 frequency points

[3] 張進(jìn), 葉中付, 汪彥龍.基于一致聚焦的寬帶信號(hào)DOA估計(jì)方法[J].電路與系統(tǒng)學(xué)報(bào), 2011, 16(1):131-136. ZHANG Jin, YE Zhong-fu, WANG Yan-long. Direction-of-arrival estimation algorithm for wideband sources based on consistent focusing[J]. Journal of Circuits and Systems, 2011, 16(1): 131-136.(in Chinese)

[4] Wang H, Kaveh M. Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wide-band sources[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1985, 33(4): 823-831.

[5] Hung H, Kavel M. Focusing matrices for coherent signal-subspace processing[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1988, 36(8): 1272-1281.

[6] 王志朝, 張?zhí)祢U, 萬(wàn)義龍, 等. 基于寬帶聚焦矩陣和高階累積量的OFDM信號(hào)的來(lái)波方向估計(jì)[J]. 計(jì)算機(jī)應(yīng)用, 2013, 33(7):1828-1832. WANG Zhi-chao, ZHANG Tian-qi, WAN Yi-long, et al. Direction of arrival estimation of orthogonal frequency division multiplexing signal based on wideband focused matrix and higher-order cumulant[J]. Journal of Computer Applications, 2013, 33(7):1828-1832.(in Chinese)

[7] 王娟, 馮青, 吳仁彪, 等. 一種用于聲學(xué)成像的穩(wěn)健寬帶恒定束寬波束形成方法[J].西安電子科技大學(xué)學(xué)報(bào):自然科學(xué)版, 2007,34(1):154-158. WANG Juan, FENG Qing, WU Ren-biao, et al.A robust wideband constant-beam width beamforming method for acoustic imaging [J]. Journal of Xidian University: Natural Science, 2007, 34(1)：154-158.(in Chinese)

[8] 朱維杰. 寬帶水聲陣列信號(hào)處理的原理方法及應(yīng)用[D].西安:西北工業(yè)大學(xué), 2003. ZHU Wei-jie. Study on principle and method of broadband underwater acoustic array signal processing[D]. Xi’an: Northwestern Polytechnical University, 2003.(in Chinese)

[9] Claudio E D, Parisi R. Waves: weighted averages of signal subspaces for robust wideband direction finding[J].IEEE Transactions on Signal Processing, 2001, 49(10): 2179-2191.

[10] 甘甜, 王英民.一種穩(wěn)健的恒定束寬波束形成方法[J].聲學(xué)學(xué)報(bào), 2012,37(1):18-24. GAN Tian, WANG Ying-min. A robust broadband beamforming method of constant beam width[J]. Acta Acustica, 2012, 37(1):18-24.(in Chinese)

[11] 畢楊, 王英民.一種穩(wěn)健的寬帶聚焦波束形成算法[J].計(jì)算機(jī)工程與應(yīng)用, 2015, 51(4):218-221. BI Yang, WANG Ying-min. Robust broadband focused beam-forming algorithm[J]. Computer Engineering and Applications, 2015, 51(4):218-221.(in Chinese)

[12] 周琳, 黃春琳, 粟毅. 基于魯棒Capon波束形成的探地雷達(dá)成像算法[J]. 電子與信息學(xué)報(bào), 2012,34(5):1024-1029. ZHOU Lin,HUANG Chun-lin,SU Yi. A ground penetrating radar imaging algorithm based on robust Capon beamforming[J]. Journal of Electronics & Information Technology, 2012,34(5):1024-1029.(in Chinese)

[13] Stoica P, Wang Z S,L J. Robust Capon beamforming[J]. IEEE Signal Processing Letters, 2003, 10(6):172-175.

[14] 馬遠(yuǎn)良, 劉孟庵, 張忠兵, 等. 淺海聲場(chǎng)中拖曳線列陣常規(guī)波束形成器對(duì)本艦噪聲的接收響應(yīng)[J]. 聲學(xué)學(xué)報(bào),2002, 27(6): 481-486. MA Yuan-liang, LIU Meng-an, ZHANG Zhong-bing, et al. Response of the towed line array to the noise of the tow ship in shallow water[J]. Acta Acustica,2002, 27(6): 481-486.(in Chinese)

[15] Ma Y L, Liu M A, Zhang Z B, et al. Receiving response of towed line array to the noise of the tow ship in shallow water[J]. Chinese Journal of Acoustics, 2003, 22(1): 1-10.

[16] 夏麾軍,馬遠(yuǎn)良,汪勇,等. 高增益對(duì)角減載波束形成方法研究[J]. 聲學(xué)學(xué)報(bào),2016,41(4):449-455. XIA Hui-jun, MA Yuan-liang, WANG Yong, et al. Study on diagonal reduced load beamforming[J]. Acta Acustica, 2016,41(4):449-455.(in Chinese)

Research on Dual Optimized Broadband Beamforming Algorithm

BI Yang1,2， WANG Ying-min2，WANG Qi2

(1.School of Electronic Engineering, Xi’an Aeronautical University, Xi’an 710077, Shaanxi，China; 2.College of Marine, Northwestern Polytechnical University，Xi’an 710072，Shaanxi, China)

When the focusing matrix is identified in the coherent signal-subspace method, the deviation of the initial direction and the deviation of focusing frequency selection have an effect on the final focusing effect, even making the algorithm fail. A dual optimized broadband beamforming algorithm is presented. The algorithm is to use the robust Capon beamforming algorithm to correct the focusing matrix, the broadband signals are focused on the best focusing frequency by the corrected focusing matrix, and the narrowband signals are beamformed by the second-order cone programming algorithm. The computer simulation results and lake experiments show that the proposed algorithm can make the beam constant, and lower the sidelobe level at each frequency point.

acoustics; focusing matrix; focusing frequency; robust Capon beamforming algorithm; second-order cone programming; broadband beamforming

2016-11-15

畢楊(1981—)，女，講師，博士。E-mail:biyangg@163.com

TN929.3

A

1000-1093(2017)08-1563-09

10.3969/j.issn.1000-1093.2017.08.014