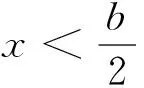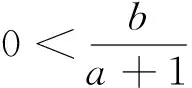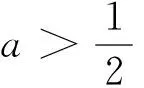例析充要條件在數學解題中的導向性

江蘇省蘇州實驗中學 (215000)

董逸婷

例析充要條件在數學解題中的導向性

江蘇省蘇州實驗中學 (215000)

董逸婷

高中數學經歷了多次課程改革，充要條件的內容都做了保留甚至是強化.2003年《普通高中數學課程標準(實驗稿)》中“常用邏輯用語”作為單獨一章被列入選修1-1、選修1-2中.充要條件是一種邏輯思維方法.但是，反觀我們的教學，一般都詳細講解了充分條件、必要條件的含義及判斷方法，而弱化了充要條件在解題時的向導作用.本文筆者從運用充要條件優化解題策略方面談談粗淺的看法，以期拋磚引玉.

利用結論成立的必要條件優化解題過程

例1 設0(ax)2的解集中的整數恰好有三個，求實數a的取值范圍.

含參整數解問題一直是不等式的一個難點.學生處理時往往不能準確的進行條件轉化.如本例的充要條件也很難一步到位.遇到此類問題我們可以先把條件弱化，求出問題弱化后的參數a的取值范圍，即原問題的一個必要條件，再在這個必要條件的基礎上尋找突破口，進一步探究原問題的充要條件，從而求出參數的取值范圍.

首先，將不等式(x-b)2>(ax)2先轉化為(a2-1)x2+2bx-b2<0(*)

因為0-1.此條件為題目的第一個必要條件，利用該條件，可以局限住參數a的取值范圍，有效縮小了a的討論范圍.

下面問題轉化為了假二次不等式的整數解問題.現將問題弱化成不等式有解：

①當-1

因為a>1，所以2a-2

又已知0

回顧本題解題過程，解題的關鍵是利用二次函數圖像求出恰有三個整數解的一個必要條件a>1，在這個必要條件下得出原不等式的解集是一個開區間，再在這個必要條件下，求出區間右端點只能在某一個小區間內活動，從而由已知可以確定這個區間的三個整數，進而得出這個區間左端點的活動區范圍，列出不等式，求出參數范圍.充分體現了必要條件的解題功能.

解題過程中如能合理利用題中的必要條件，首先縮小題設參數范圍，再在該范圍下討論，可以極大減少分類討論情況，降低解題難度.如下例,2008年江蘇卷填空第14題：

例2 設函數f(x)=ax3-3x+1(x∈R)，若對于任意x∈[-1,1]，都有f(x)≥0成立，則實數a的值為 .

命題者將此題放在填空的最后一道題，作為把關題.乍一看，這類問題很容易想到求f(x)=ax3-3x+1,x∈[-1,1]的最小值；或者利用參數分離法，注意到x∈[-1,1]，必須分類討論，求參數分離后的函數的值域或最值.無論哪種方法，都會消耗學生太多時間與精力.如能從另外一個角度考慮，先嘗試求它的必要條件，再進行下一步研究：

顯然，必要條件的利用得到了意想不到的簡化作用.

2.利用結論成立的充分條件優化解題過程

例3 設函數f(x)=ex-1-x-ax2.

(1)若a=0，求f(x)的單調區間；

(2)當x≥0時，f(x)≥0，求實數a的取值范圍.

本題第一問是常規的單調性計算，通過求導可得f(x)在(-∞,0)上單調遞減，在(0,+∞)上單調遞增.

第二問常見方法有兩種：一是分類討論的方法，可能會出現不知如何分類，或者分類太多，不容易找到分類標準；二是分離參數法，只需求出參數分離后的函數的最值或值域即可.但是，參數分離后的函數的值域或最值求解時可能比較困難，需要對函數多次求導或借助高等數學中的洛比達法則，這也明顯超出了中學數學的范圍.這種情況如果我們可以有意識合理的使用題目的充分條件優化解題過程，可以極大降低題目解答的復雜性.

分析本題，依題當x≥0時，f(x)≥0，即f(x)=ex-1-x-ax≥0，而f(0)=0.即f(x)≥f(0).如果可以證得f(x)在(0,+∞)上單調遞增，即f′(x)=ex-1-2ax≥0，則結論成立.

本題是可以直接對a進行分類討論求解不等式恒成立問題的，但是上述解法先探求結論成立的充分條件，再證明其必要性.這種方法操作性很強，不失為處理該題的一種妙法.

前蘇聯大教育家贊可夫強調知識間的聯系，他認為，“聯系的確立，并不是因為材料的各個片段的學習在時間上相近，而是因為材料的各部分之間每一種關系本身在學生知識體系的形成過程標志著前進的運動”.邏輯從內容上看似乎很獨立，在高考中看似也只體現在一個填空題或是第15題中一部分，但是它是一種辯證的思維方法，是各部分知識的紐帶.

反觀上述幾例，充要條件作為邏輯思維方法，在解題中形成策略，其解題策略在數學中廣泛應用.如在例1中，先討論不等式有解，再討論有有限個整數解；例3中先求出其充分條件，即使函數在定義域上單調時a的范圍，再證明其必要性，避免了含參討論.另外，在函數一章中，對于含參不等式恒成立，求參數取值范圍一類問題時，也可利用特殊值法先求出其充分條件，局限范圍后再討論.

因此，在平時教學中，應該重視充要條件在解題導向性中的應用，特別是在高三專題復習時尤其注意其作為解題策略的重要性，指導學生合理利用題目充要條件突破難點，培養學生辯證思維的能力.