生成性教學的“偽”與“真”

廣東省梅州市梅縣區高級中學 (514011)

李浩然

生成性教學的“偽”與“真”

廣東省梅州市梅縣區高級中學 (514011)

李浩然

長期以來，教師在預成性思維的指導下，形成了靜態的預設性教學.教師在教學過程中嚴格按照課前預設進行教學，教學活動以教師的教為主線，考慮的是教師應該教什么，怎么教，很少考慮學生想學什么，怎么學，學生沒有決定權，甚至沒有發言權，導致學生思維僵化，使學生不能成為學習的主人.在批判傳統教學過分預設的基礎上，新課程強調知識的生成過程，師生的交往互動以及成長的價值追求，從而凸顯出教學的生成性特點.

1 生成性教學的內涵

生成性教學是在彈性預設的前提下，在教學過程中充分利用各種資源，根據不同的教學境況，靈活地進行教學活動，鼓勵學生對所學數學知識進行自我理解、自我解讀，尊重學生的個人感受和獨特見解，循著教學→生成→利用→再生成→再利用這一動態演進路線，在生成和利用的反復交替中，不斷將教學過程向縱深推進，推動學生的知識建構和認識的發展.

2 生成性教學的“偽生成”

新課程改革把“生成”當作自覺的價值追求，當作彰顯課堂生命活力的常態要求.生成性教學滿足了教學改革的期待，演繹了眾多“未曾預約的精彩”.但在具體實施過程中，數學課堂上卻出現“預設型生成”、“流程型生成”、“放任型生成”等“偽生成”.

2.1 預設型生成

在預設型生成中，學生自由探索的空間微乎其微，盡管賦予了學生表達的機會，可一旦與教師的預設發生沖突，教師便會用各種方式誘導學生走上早已預設好的道路，一切都必須掌握在教師預設好的計劃之中，學生實際上是被生成者、被建構者，整個教學過程缺乏學生的主動、主體角色.教師僅把“生成”作為體現新課程改革理念的手段以便迎合外界的評價，但實質仍將學生視為被動接受知識的容器，仍然屬于傳統的預設性教學.

2.2 流程型生成

數學課堂教學“隨時都有可能發現意外的通道和美麗的圖景，而不是一切都必須遵循固定線路而沒有激情的行程”(葉瀾).然而，有些教師將生成從由以產生的情境中剝離出來，使之流程化，使生成性教學陷入一種固化模式.該模式規定教師“應該做什么、不該做什么，先做什么、后做什么”，還限定了各類活動的時間，要求教師按照固定的流程去實施，強調的是套路與流程，從而限制了教師的積極性和創造性，壓制了學生的生命活力和個性化發展.

2.3 放任型生成

在放任型生成中，教師不顧教學目標與學科內容的特點，對生成性教學進行簡單化的處理，在教學過程中放任學生隨意生成，不加干預，失去了教師的主導作用.盡管教學形式上表現出學生的主動表達及交流，但由于學生身心發展的不完善性、不成熟性等特點，如果放任學生的課堂行為，很難達到預期的教學效果.放任型生成只追求形式上的學生生成活動，不顧生成的過程與結果，其結果不僅無法使師生達到理解與對話，其間也很難見到學生理智的探索及思維的碰撞.這樣的生成不是真正生成性教學意義上的生成.

3 從“偽生成”走向“真生成”

有效的數學課堂教學必然遠離“偽生成”，呼喚“真生成”.那么如何利用數學課堂教學進展中的各種資源，靈活處理，從而生成教學活動，還課堂以“真生成”的魅力？

3.1 錯誤中引出生成，對話中促進生成

學生不出錯的課堂，不是真正的課堂.然而，“學生的錯誤都是有價值的(布魯納)”，教師要在數學課堂上抓住學生“錯誤”的時機，巧妙、合理地處理好學生的“錯誤”這一教學資源，從學生的認知規律出發，正確引導對錯誤的分析，從糾錯中體驗快樂和成功.而在析錯、糾錯過程中可產生多種對話形式，通過師生互動和反饋，最終建構知識的意義，同時促進新問題的生成，使數學課堂更加真實、靈動、精彩.

師：請同學們認真思考這個問題怎么解決.

師：請大家分析以上解法對嗎？

師：但生1的解題過程沒有問題呀.(讓學生自己發現問題)

師：說說你的解題過程.

該題通過學生的出錯——析錯——糾錯得到解決，至此，課堂已達到“利用邊化角解決問題”的教學目標，筆者準備開始新的內容，生5突然舉手.

生5：老師，我用的是另一種方法.

師：好，說說看.

師：很好！直接利用邊的關系來求.

筆者剛講完，另一位同學迫不及待地說：“老師，有更簡單的方法，我是利用圖形解的，但不知對不對.”

“說吧!”筆者鼓勵道.

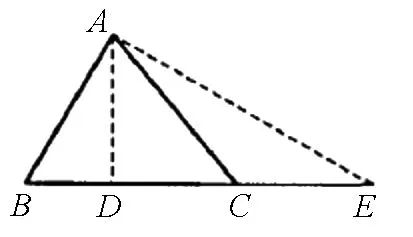
圖1

生6剛講完，熱烈的掌聲就響起來.無疑，同學們在欣賞這個簡潔、富有創造性的解法.

通過利用學生“錯誤”資源，使整個數學課堂進入一個“對話——生成——獲得”的良性循環，學生在自主探索中找到了學習的樂趣，成為學習的主人．

3.2 疑惑中驅動生成，解惑中創生生成

數學課堂中學生常常會產生各種疑惑，這些真切的疑惑，往往是豐富教學內容的新的生長點，借機創生生成，不僅能夠滿足學生解惑的愿望，而且可以引導學生在認知沖突中投入學習.因此，數學課堂上教師要善于利用學生生成的各種有用的疑點，借題發揮，在引導學生深入思考疑點的過程中推進教學進程.

案例2 已知橢圓5x2+6y2=30的左、右焦點為F1、F2，P是橢圓上一點，且∠F1PF2=60°，求ΔF1PF2的面積.

師：說說你的解法.

生1用的是通法且過程無誤，而整體求解的過程也無誤，結果卻大相徑庭，孰對孰錯？不僅學生充滿疑惑，筆者也感到奇怪與不解.

師：我們共同探討問題出在哪里?

生3：從圖形上看∠F1PF2不可能是60°.

師:該如何證明∠F1PF2不可能是60°?

師：解釋得很好！原來此題無解是命題者疏忽所致.

筆者還就此引申：(作為課外思考題)

學源于思，思源于疑.學生在學習時常常產生諸多疑問.教師要營造寬松、民主的教學氛圍, 因勢利導，順水推舟，在疑問中驅動生成，在解惑中創生生成，以促使學生思維通暢，主動建構.

3.3 求異中激起生成，探究中尋求生成

課堂中經常容易生成一些不成熟的看法或有待求證的認識，這些生成的看法、認識雖不是“知識創新”，卻可能是啟動一個新的探究過程的觸發點，教師應及時引導學生“探一探”，追根究底地將學生的思維引向深入，讓學生在“探個究竟”中獲得知識.

n·2n-1(n∈N*).

經過師生的分析討論，分別采取“利用二項式定理”、“倒序相加法”、“數學歸納法”證明了該恒等式，這正是筆者課前的預設.至此，筆者正準備下一教學環節，而前排的生1輕聲問道：“老師，能不能用賦值法來證明？”筆者覺得此思路可行，但是否湊效心里也沒底，筆者決定順著生1的思路“探一探”.

師：大家討論一下，能否用生1提出的賦值法來證明.

生3怯怯地說：“由2n到n·2n-1像求冪函數的導數：(xn)′=n·xn-1.”

筆者覺得在理，便鼓勵道：大家用求導的方法試試看.

生4突然興奮地說：“兩邊求導！兩邊求導可以證明！”

師：說說你的證明.

話音一落，掌聲一片.筆者也不禁為學生們的奇思妙想而拍案叫絕.

心理學研究表明，在任何人的心靈深處，都有一種迫切的需要——希望自己是一個發現者和探索者.因此，在數學課堂上應多鼓勵學生提出不同的方法、思路，不同的探求路徑，雖然這會“打亂”教學的預設，令教師始料未及，但教師如果能循著學生的思路另辟蹊徑，往往可以引出不一樣的精彩，收到意想不到的教學效果.

數學課堂教學改革所要追求的價值要旨是生成性教學，它是基于預設與生成的辯證統一的生成.所以，教師不能停留在傳統的預設性教學模式上，也不能追求只有生成的課堂，而應該機智地安排數學課堂的教學內容，科學的看待預設性教學，并將其正確地引領到生成性教學的道路上來，超越“真預設”，追求“真生成”.

[1]趙緒昌.例談生成性教學資源的利用策略[J].中國數學教育(高中版)，2012,5.

[2]馬玉琪.教學生成與生成教學[J].上海教育科研，2012,10.

[3]郭少英，朱成科.生成性：當代課堂教學改革的旨趣[J].遼寧教育，2014,3.