多指標(biāo)面板數(shù)據(jù)因子分析方法研究

李 鵬

(福州大學(xué)經(jīng)濟與管理學(xué)院 福建 福州 350116)

?

多指標(biāo)面板數(shù)據(jù)因子分析方法研究

李 鵬

(福州大學(xué)經(jīng)濟與管理學(xué)院 福建 福州 350116)

目前，國內(nèi)學(xué)者在多指標(biāo)面板數(shù)據(jù)因子分析方面的研究較少，而面板數(shù)據(jù)是常用的一種數(shù)據(jù)形式，因子分析是常用的一種綜合評價方法。本文把多指標(biāo)面板數(shù)據(jù)和傳統(tǒng)因子分析結(jié)合起來，將面板數(shù)據(jù)各個時間截面數(shù)據(jù)按時間順序平鋪展開形成一個大截面數(shù)據(jù)，然后對此進行傳統(tǒng)因子分析，減少了因子分析的次數(shù)，也能提取多指標(biāo)面板數(shù)據(jù)的重要信息。

多指標(biāo)；面板數(shù)據(jù)；因子分析

一、引言

因子分析在1904年由Chales Spearman提出，它將多個變量綜合為少數(shù)幾個因子。目前，它的主要有兩個應(yīng)用：一是得到因子得分進行排序，即將多個變量降維成一個綜合的變量，該變量保留了之前多個變量的所有信息，可以根據(jù)該變量的大小對評價對進行排序；二是對因子進行分類，即根據(jù)相關(guān)性大小把原始變量分組，使得同組內(nèi)的變量之間相關(guān)性較高，而不同組的變量之間相關(guān)性則較低。

二、面板數(shù)據(jù)的數(shù)字特征

(一)單指標(biāo)面板數(shù)據(jù)

單指標(biāo)面板數(shù)據(jù)的數(shù)據(jù)格式可用二維表或者矩陣表示。

設(shè)總體共由N個樣品,每個樣品的特征用一個指標(biāo)X來表示，時間長度為T，則Xi(t)表示第i個樣品在t時間的指標(biāo)值。

截面數(shù)據(jù)的數(shù)據(jù)格式也是用一個二維表來表示的，設(shè)總體共由N個樣品，每個樣品的特征用p個指標(biāo)來表示，則Xij表示第i個樣品第j個指標(biāo)的數(shù)值。

(二)多指標(biāo)面板數(shù)據(jù)

1.多指標(biāo)面板數(shù)據(jù)的數(shù)據(jù)格式

多指標(biāo)面板數(shù)據(jù)的結(jié)構(gòu)要復(fù)雜一些,不同于單指標(biāo)面板的數(shù)據(jù)可以由一個簡單的二維表來表示，用三維表來表示。多指標(biāo)面板數(shù)據(jù)除了具有截面維度和時間維度外,還增加了指標(biāo)維度，因此多指標(biāo)面板數(shù)據(jù)實際上是一張三維表格，如表1所示。研究總體共有N個，每個樣品的特征用p個指標(biāo)表示(X1,X2,…,Xj,…,Xp)，時間長度為T,則Xij(t)表示第i個樣品第j個指標(biāo)在t時間的數(shù)值。

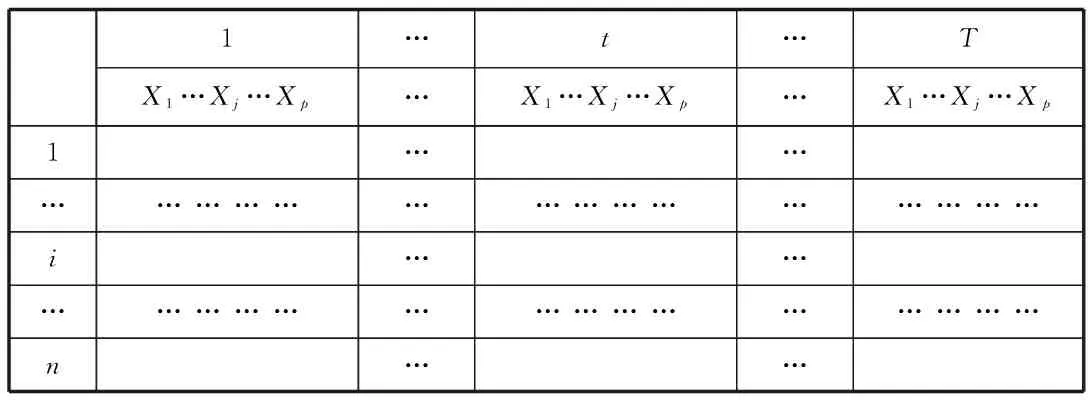
表1 多指標(biāo)面板數(shù)據(jù)[1]

矩陣表示為：

2.多指標(biāo)面板數(shù)據(jù)的幾個統(tǒng)計量

下面給出多指標(biāo)面板數(shù)據(jù)的幾個統(tǒng)計量，在多指標(biāo)面板數(shù)據(jù)因子分析中需要用到這幾個統(tǒng)計量。

(1)第j個指標(biāo)的均值

(1)

(2)第j個指標(biāo)在t時間的均值

(2)

(3)第j個指標(biāo)的方差

(3)

(4)第j個指標(biāo)在t時間的方差

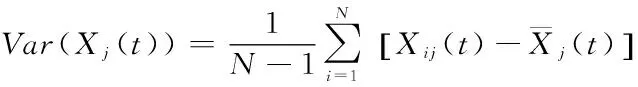
(4)

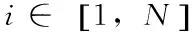
三、傳統(tǒng)因子分析方法步驟

設(shè)X=(X1,…,Xp)’是觀測的隨機向量。

傳統(tǒng)因子分析的基本步驟如下[2]：

(1)計算樣本均值和樣本方差

(2)原始數(shù)據(jù)標(biāo)準化

由于研究問題中所選取的各個指標(biāo)的單位可能存在差異。為了消除不同指標(biāo)之間由于量綱不同造成的誤差，使評價指標(biāo)相互可比，因此須對各指標(biāo)的原始數(shù)據(jù)進行標(biāo)準化處理，最大程度減小研究結(jié)果的誤差。數(shù)據(jù)標(biāo)準化之后，得到相關(guān)系數(shù)矩陣R。

(3)適用性檢驗

因子分析方法的核心思想之一是對原有指標(biāo)進行縮減，從原始變量中的信息重疊部分提取因子，以達到減少變量個數(shù)的目的。因此，因子分析方法要求原始變量之間有較強的相關(guān)關(guān)系。通常使用KMO檢驗和巴特利特球型檢驗等方法對變量之間相關(guān)性進行檢驗，當(dāng)指標(biāo)具有統(tǒng)計顯著性時，則表示通過了因子分析模型的適用性檢驗。

(4)求相關(guān)系數(shù)矩陣R的特征值和標(biāo)準化特征向量

記λ1≥λ2…≥λp≥0為R的特征值,其相應(yīng)的單位正交特征向量為l1,l2,…,lp。

(5)求因子的載荷矩陣A

求出各個因子載荷的值是運用因子分析進行綜合評價的關(guān)鍵，常用的因子載荷求解方法包括主成分分析法、主軸因子法、最小二乘法、極大似然等。

根據(jù)累計貢獻率要求確定因子載荷矩陣,確定公因子的個數(shù)m。

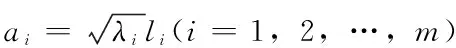
(6)求因子得分和綜合得分

在建立起因子模型之后，則需要考察模型每一個變量之間的相互關(guān)系，那么就需要計算因子得分來實現(xiàn)這一目的。因子得分就是指公共因子在每一個變量上的得分，這需要找到提取公共因子時用原始變量和公共因子之間建立的線性表達式，通過將原始變量的標(biāo)準化數(shù)據(jù)值代入表達式中，就可以求出各個因子的得分。

[1]王培,王焱鑫,崔巍.面板數(shù)據(jù)的因子分析[J].貴州大學(xué)學(xué)報(自然版),2009,26(6):10-13.

[2]王學(xué)民.應(yīng)用多元分析[M].上海財經(jīng)大學(xué)出版社,2014.

[3]董鋒,譚清美,周德群.多指標(biāo)面板數(shù)據(jù)下的企業(yè)R&D能力因子分析[J].研究與發(fā)展管理,2009,21(3):50-56.

[4]任娟.多指標(biāo)面板數(shù)據(jù)融合聚類分析[J].數(shù)理統(tǒng)計與管理,2013,32(1):57-67.

李鵬(1990-)，男，漢族，湖北荊門市人，管理學(xué)碩士，福州大學(xué)經(jīng)濟與管理學(xué)院，研究方向：創(chuàng)新管理與評價。