親歷過程??建立模型

陳麗娟

“圓環的面積”是人教版第十一冊第五單元的知識，主要目標是：讓學生認識圓環，了解并掌握圓環的特征和圓環面積的計算方法。教材的例題極其簡單（如圖1所示）：

我看到這個例題的第一個想法是太簡單了，不就是用外圓面積減去內圓面積求出圓環的面積？可是越深入備課越能領會新課程的理念：思想比公式更重要，建模比計算更重要。以往我們的課堂重在知識的傳授、技能的訓練，忽視了數學思想實質。本節課我們不應將會計算圓環面積作為終極目標，而要引導學生在掌握圓環面積計算方法的基礎上，深度思考，使學生感受到知識之間的內在聯系，領悟數學模型之妙。鑒于學生在實際生活中對環形已有大量的接觸，但對圓環的形成過程甚少感悟；學生對計算圓環面積能夠盡快掌握，卻對以此類教學模型解決實際問題不能運用自如，因此我進行了教學設計與實踐。下面我結合“圓環的面積”的教學實踐，談談如何引導親歷過程，建立模型。

一、欣賞圖片，初步感知身邊的圓環

課程改革以來，大家越來越強調讓學生親身經歷實踐活動，通過認知、體驗、感悟，獲得新知、技能和方法。本課一開始，我用課件逐一展示現實生活中的圖片（如圖2所示）：

課前教師收集了一些圖片，請看，這是……

看來圓環在生活中隨處可見。

通過直觀展示圖片喚起了孩子對“圓環”已有的經驗，讓學生感受在生活中到處都能接觸到圓環，將抽象的“圓環”文字變成了看得見的形象，積累這方面的經驗，可以幫助學生更好地理解概念、建構知識。

二、動手操作，親歷圓環概念的形成過程

數學新理念強調：在知識的學習過程中，應有親身體驗，只有親身經歷概念的形成過程，所學知識才能理解透徹并靈活運用。因此，我注重引導學生動手操作，親歷圓環概念的形成過程，在認識圓環的環節中給學生提供了自己創作圓環的空間，親歷圓環這個圖形的形成過程，初步感悟圓環的特點就是兩個同心圓，從外圓中減去內圓，剩下的部分形狀就是圓環。

我一方面提供給每個學生一個圓形紙片，請學生猜它的半徑，口述這個圓的面積算式，培養學生估測意識與能力，并復習本節課的基礎圓的面積計算方法。

我另一方面引導學生動手操作：剪出圓環：以O為圓心，在圓形紙片上畫半徑為整厘米的小圓，剪掉內圓，剩下的這個部分形狀是什么？（圓環，環形）思考：這個圓環是如何形成的？由于體驗了環形“再創造”的整個過程，學生能輕松自如地理解了“大圓中去掉小圓的面積就是圓環”。下一個環節“求圓環的面積”對學生來說便水到渠成。

三、直觀探究，經歷計算圓環面積的全過程

荷蘭數學家弗賴登塔爾認為：數學學習應該由學生把自己要學習的東西自己去發現或創造出來，只有實行再創造獲得的知識才能真正被掌握，被靈活運用。我長期的教學經驗積累確實反映了這一現實：學生如果被動地接受學習內容，他對學習的內容就難以真正理解，更談不上靈活運用了。

在學生自己創作出圓環的基礎上，我把三個不同的圓環用磁鐵粘在黑板上，問：這是同學剪的圓環，你認為哪個圓環面積大？

學生猜測：小圓半徑小的圓環大；第三個圓環面積大……

老師：用事實數據來說話，請算出你手中圓環的面積。

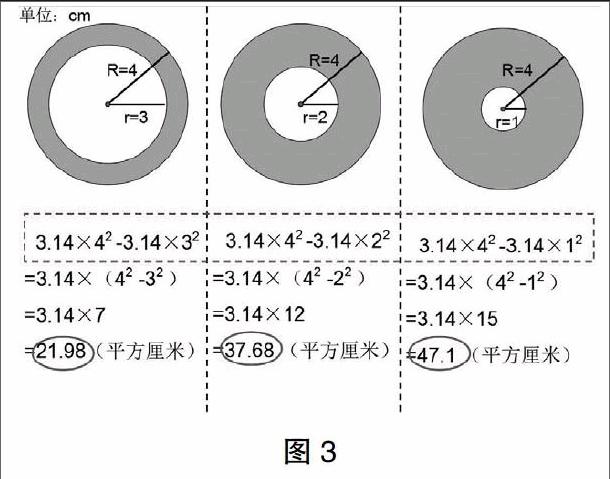
學生獨立計算出自己手中圓環的面積并展示結果，有以下三種情況（如圖3所示）：

緊接著我引導學生觀察思考：請看這三個算式，你發現了嗎？求圓環面積都是用……？（外圓面積減內圓面積得到圓環的面積。）

我繼續引導學生更深層次的思考：既然都用外圓面積減內圓面積得到圓環的面積。那為什么我們計算出來的圓環面積最后結果不一樣？有的學生說挖去的小圓面積小，所以圓環面積大；有的學生認為第三個的環寬最大，所以圓環面積最大。這時老師順勢出示了學生的錯例：3.14×（4-3）2=3.14（平方厘米）。

教學內容傳達給教師的是一道道例題、一個個知識點，我們要領會教材內涵，依據課堂學生的實際學習情況，找到知識的生長點與發展點，引導學生自己思考、探索，在經歷、感受中體驗著知識的建構過程。教學中，發現求圓環的面積時部分學生會用π乘環寬的平方，怎樣讓學生理解這種方法的錯誤呢？我設計了常見的環寬相等的箭靶（如圖4所示），直觀感知、并提供數據計算不同環的面積，對比發現明明每一環大小不一樣，如果用3.14乘環寬的平方求圓環的面積所有結果卻都相等，從而證明這是不可行的，圓環的面積只能是外圓面積減內圓面積。并且解釋了在賽場上射中不同環的得分不一樣的原因。

這樣引導學生參與計算圓環面積的全過程，在活動中體驗，在對比中思考，在思考中領悟掌握知識，學習活動慢慢內化成學生的心智活動，學生學習有動力有創造，思維得到發展，數學思想方法得以滲透。

四、拓展延伸，構建求組合圖形面積的一般模型

教學過程中，我們還要注重對學生的感性體驗適時地進行概括和提升，促進學生方法掌握。在學生理解掌握了圓環的概念、圓環面積的計算之后，我們要針對這類圖形建構數學模型，掌握這類圖形的解題策略。

本課最后的拓展延伸，以課件形式逐一展示下列圖形，讓學生口述每個圖形陰影部分面積的計算方法，并歸納總結計算方法的相同之處（如圖5所示）。

以上題目雖然不是圓環的面積，但求這樣的兩個圖形之間陰影部分的面積都可以運用“外面圖形面積—里面圖形面積”這一模型進行解答，拓展了計算組合圖形面積的一般方法，成功地構建數學模型。之后我們用數學模型來解決生活中的實際問題，以實現“形式的”數學知識向現實生活的“復歸”，也就是在“學”與“用”之間為學生搭建起了一座無形的橋梁，學生解答數學問題才能得心應手，感受數學思想方法的無限魅力。

本節課通過讓學生觀察生活中的圓環、動手創作圓環、探究圓環的面積計算方法，最后延伸到計算組合圖形面積的一般方法，一步一步引導學生經歷了知識形成的過程，將知識進行內化，不斷完善。也許圓環的面積這個知識很淺，但我們要教得厚實，讓學生在經歷再創造的過程中感受建模的力量。

（作者單位：福建省莆田市荔城區梅峰小學 ）