對考查向量的試題背景分析與教學備考建議
上海市第四中學 …周 科
對考查向量的試題背景分析與教學備考建議
上海市第四中學 …周 科
《上海市高中數學學科教學基本要求》(試驗本)以及《普通高等學校招生全國統一考試上海卷考試手冊》都強調對學生創新意識和創新能力的考查,考查的目的是基于強調培養中學生的個性品質,開拓中學生的數學視野,促進中學生理性思維的逐步形成。多年來,上海的高考試卷命制過程中都希望所命制的試卷能很好地貼切這一考查要求,通過命題專家的努力,這些年的數學高考卷都出現了很多具有創新性的試題。但這些好題也恰恰是學生難以逾越的一道道坎,這一方面暴露出當前數學教學中知識遷移、組合、融匯的程度不高,能力區域不寬泛,創新意識不強,同時,學生也沒能很好地發揮數學基本思想、基本方法在這類題中的基礎性、工具性作用。本文僅就向量及其應用中的問題,通過幾個典型例題做一個探究。
一、向量題的考查特點分析及典型例題剖析
1.以向量為背景,考查三角函數
依據《上海市中小學數學課程標準(試行稿)》及其調整意見和高考選拔人才的選拔要求,結合中學教學實際,考試旨在考查學生的數學素養。如何在三角函數、向量這些傳統意義下的中低檔試題中進行能力立意呢?近幾年的上海卷給出了較為滿意的回答。譬如:
例1 (2016年高考數學上海卷理科第12題)在平面直角坐標系中,已知上的一個動點,則的取值范圍是。
試題分析:本題利用數形結合思想,將問題轉化到單位圓中,從而轉化成平面向量的坐標運算,利用三角函數的圖象和性質,得到的取值范圍。主要考查了考生的邏輯推理能力、基本運算求解能力、數形結合思想、轉化與化歸思想等。
2.以向量為背景,考查函數的值域
高考命題以基礎知識為載體,結合對基本思想、基本方法與技能的考查,突出考查學生分析問題、轉化問題、解決問題的能力,在解題思路和方法的尋找上突顯學生的數學素養。近幾年高考數學上海卷在這一點上做得比較成功。譬如:
例2 (2012年高考數學上海卷理科12題) 在平行四邊形ABCD中,邊AB、CD的長分別為2、1,若M、N分別是邊BC、 CD上的點,且滿足的取值范圍是。

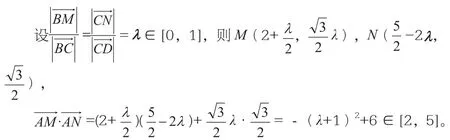
解法1是用向量的數量積運算,將其轉化為函數問題;解法2是采用“建系”,用平面向量運算的坐標表示轉化為函數問題。本題較好地考查了學生用數學基本知識和技能解決數學問題的能力。
3.以向量為背景,考查概率
高考命題要遵循《考試說明》,在高考數學《考試說明》中提出試題具備高信度、效度、必要的區分度和適當的難度。傳統涉及概率的試題一直是單一知識點,將向量和概率相結合,較為充分地踐行了這一宗旨。
例3 (2016年高考數學上海卷理科第14題) 如圖,在平面直角坐標系xOy中,O為正八邊形的中心,,任取不同的兩點點P滿足則點P落在第一象限的概率是
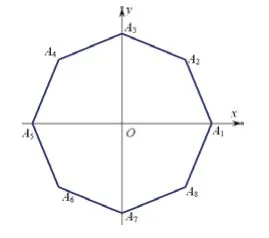
試題分析:本題主要考查古典概型概率的計算。解答本題的關鍵在于能準確確定所研究對象的基本事件空間、基本事件個數,利用概率的計算公式求解。本題能較好地考查考生的數學應用意識、基本運算求解能力、數形結合思想等。
4.……以向量為背景,考查解析幾何中存在性問題
例4 (2014年高考數學上海卷理科第14題) 已知曲線若對于點存在C上的點P和 L上的點Q使得的取值范圍為。

本題考查了兩個基本能力:推理論證和運算求解。運算能力是思維能力和運算技能的結合,提高運算求解能力的關鍵是“算理”,要讓思在算之前,通過思明確算的方向,并對運算結果有一定的預見性。
5.以向量為背景,考查多變量問題
現在已進入大數據的信息化時代,高考試題也順應這一變化,命題時除了設置一些“三基”試題外,也設置了一些信息量大、多變量的問題。譬如:

本題信息量大,綜合性強,思維要求高,考查學生對信息的提取和處理能力,考查學生運算求解能力和分析、解決問題的能力。
二、備考建議
1.注重基礎,加強知識交匯性訓練
結合近幾年上海卷對向量知識點的考查特點,在向量復習中要注重對基礎知識的內在挖掘,考查知識的交匯性問題比較多,因而在課堂教學中,我們要注重基礎知識,加強能力培養,從注重學習結果向注重學習過程轉變,要從學會轉向會學,要讓學生從被動接受轉向主動發現,要從信息單向傳遞轉向信息多向交流,以適應課程改革的新要求。
2.重視數學思想方法的應用,培養學生運算能力
解決數學問題是離不開數學思想方法的,數學思想方法在解決問題中有著舉足輕重的地位,方法選擇得當,往往有出奇制勝的效果,方法思路混亂,可能導致思維受阻。另外,要加強學生運算能力的培養,有不少學生就是因為運算能力不強導致計算錯誤,進而影響解題的進度,使得解答陷入困境。
3.解題思路的生成才是教學的重點
高三主要是解題教學,解題教學就是教會學生學會如何解題、怎樣解題,而不是只給學生講題、把題講明白、把題講懂。高三教學中教學時間緊、任務重,總感覺時間不夠用,課堂上師生都有些囫圇吞棗——基礎教學不夠扎實,例題、習題的講解更是急于求成,教師往往不注重“解題思路的生成過程”的分析、傳授、講解,而過多地關注或停留在答案和解題上。著名教育學家波利亞的解題理論告訴我們:解題要做到“七分構思(讀題、審題、發散、聯想、歸納),三分表述(書寫、運算、訂正、反思與回顧)”;解題無外乎就是“架起由已知通向未知的橋梁,橋梁承載著數學知識、思想、方法、能力、技巧”。教學中教師必須清楚“我講明白,不等于學生明白,更不等于學生理解、掌握和熟練運用”,加強解題教學的過程分析、注重解題思路與脈絡生成的傳授是教會學生的關鍵。
4.適當加大向量的研究難度,突出其工具性
從近幾年的高考試題來看,有關向量的考查難度呈不斷增大的趨勢。向量是代數和幾何的橋梁,向量既可作為表達問題的工具,也可作為解決問題的工具,本文例3中的向量兼備兩者的功能。
5.加強對上海卷考試大綱和考試說明的研究
高考命題的指導思想之一,是突出對數學基礎知識、基本技能、基本思想方法的考查。《考試說明》中對知識的考查要求依次分為三個層級:記憶水平;解釋性理解水平;探究性理解水平。考試要求對向量的考查要求為:(1)解釋性理解平面向量分解定理,會求向量的長度及夾角,懂得運用向量方法進行簡單的幾何證明;(2)探究性理解向量的數量積運算及其性質,平面向量的坐標表示,會用坐標討論兩個向量的平行或垂直。在復習過程中要依據學科基本要求和考試說明,仔細推敲、認真研究、全面鋪開,不放過任何一個可能考查到的知識點,注重在知識交匯處設置問題,培養學生處理綜合問題的能力。
6.注重回歸課本,加強對往年試題的研究
課本是教學之本,在最后的復習過程中,一定要加強對課本習題、重點例題的探究,注重對教材的挖掘和利用,許多好的高考試題都源于教材而高于教材,是對教材的二次開發和再利用,因此一定要用好教材,加強對課本的研究。
[1]2017年《普通高等學校招生全國統一考試上海卷考試手冊》
[2]過家福,王華民.三角函數、向量試題特點及應對策略[J].中學數學教學與參考,2017(5).
[3]胡書軍,李素香,霍紅梅.解題思路的生成才是解題教學的重中之重[J].中學數學教學與參考,2016(5).

