利用變式教學開闊學生思維
廣西博白縣旺茂鎮第一初級中學 吳世明
利用變式教學開闊學生思維
廣西博白縣旺茂鎮第一初級中學 吳世明
自初中數學課程改革實施以來,如何提高課堂教學的有效性成為教師關注的熱點。教師的智慧體現在其靈活多變的教學過程中。教師上好一堂生動、有趣而富有感染力的課,學生將受益匪淺。而學生作為教學的主要對象,教師應綜合運用多種方法,引導學生去主動探究問題。因此,變式教學將會成為課程改革發展的必然趨勢。
初中數學;變式教學;思維能力
所謂“變式教學”就是將數學問題進行不同角度、不同層次以及不同背景的變式,以達到揭示問題本質的教學目的。利用“變式教學”模式,可以將學生的思維向著“寬”和“深”的方向發散,為學生減輕學習壓力,通過一個問題解決一類問題,進而提高課堂效益。
一、一題多解,提升思維敏捷性
在“變式教學”過程中,教師要不斷培養學生思維的轉換能力,“一題多解”可以將學生的思維發散,不斷啟發學生從多個角度、不同層面去觀察、思考一道題,學生的思維能力就能得到實際鍛煉,獨自探究的意識也會得到加強。
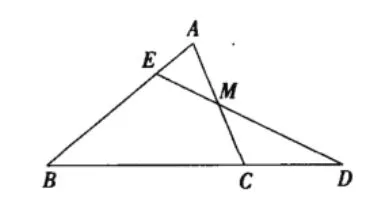
例如:如圖所示,已知在△ABC中,M是AC邊的中點,E是邊上的一點,且AE=AB,連接EM并延長,交BC的延長線于點D。求證:BC=2CD。
這是一道典型的幾何證明題,學生們在求證前要仔細閱讀題目給出的條件,理清思路。此題的解法眾多,如過點C作CF//AB交DE于點F,于是可以證明△AEM≌△CFM,從而由△CDF≌△BDE,就可以得到C=2CD。接著我又給學生們引薦了一種方法,取AB的中點F,連接CF,可以知道E是AF的中點,從而可以證明BC=2CD。類似取中點的方法還有許多,譬如取AB的中點F,連接FM、FC,于是可以證明四邊形CDMF是平行四邊形,從而再證得CD=FM=即BC=2CD。此題可以做三角形中位線,結合三角形的全等,三角形的相似,相似三角形的比例以及平行四邊形等解法,是一道典型的“一題多解”題,對于鍛煉學生的思維能力有極大的幫助。學生在做此道題的時候,教師首先應要求每一位學生拿出多種解法,而后讓學生之間互相進行交流、討論,最后共同做出總結,促進學生在學習過程中收獲更多的知識。
可見“一題多解”在初中數學教學中的重要位置。所以,教師要不斷地啟發學生,努力增強學生對學習的興趣與自信心,提升學生思維的敏捷性。同時,學生們在平時的練習中也要形成“一題多解”的意識,不拘泥于一種方法,努力挖掘自己的思維潛能,為后續的數學學習奠定堅實基礎。
二、一題多變,點燃思維靈感
“一題多變”就是將題目的條件、圖形的位置或者條件與結論等進行變形,然后重新組合成一個題型的解題方法。“一題多變”對學生的知識能力進行了鞏固性訓練,增添了學生在學習過程中的趣味性,喚醒了學生的求知欲望,促使學生樂于去研究此類題型。深刻剖析“一題多變”類題型可以鍛煉學生的思維邏輯,將題目化簡,從而達到舉一反三的效果。
此類題是關于求解取值范圍類的題型,在原始的例題中,是關于二次根式有意義,求x的取值范圍。接下來的幾個變式是關于例題的幾個變式,逐步將難度加深,一步步地加深題型的難度,也會讓學生逐步產生難題意識,尤其是在變式3中,通過對前面幾個變式的求解過程,學生更加容易找到求解變式3 的方法,大大縮小了變式3的難度,使得學生順利求解出正確答案!
通過“一題多變”的形式去改變教學的方式,不僅降低了題目的難度,而且大大地激發了學生的獨立思考與探究的興趣,有利于活躍課堂的氣氛,點燃學生的思維靈感。
三、一法多用,以不變應萬變
“一法多用”是對“變式教學”解決問題的方法加以總結與歸納,進而形成某一種技巧的解題方式。通過這種技巧的學習可以達到多題歸一的目的,使學生能夠迅速抓住題型的本質,將所學知識與能力的培養有效結合起來。通過“一法多用”,不但可以以不變應萬變,而且有助于學生良好學習習慣的養成,在提高課堂教學效率的同時,學生的思維廣度也得以拓展。
例如:(1)已知一元二次方程mx2-2x+1=0有兩個不相等的實數根,求m的取值范圍。(2)已知拋物線y=mx2-2x+1的頂點在x軸上,求m的取值范圍。(3)已知二次三項式mx2-2x+1在實數范圍內不能分解因式,求m的取值范圍。(4)若mx2-2x+1是一個完全平方式,求m的值。
這幾道題看似不同,其實解題方法極為相似,都是由(1)式變式而得到的,然后通過利用Δ=b2-4ac來解題。學生要深入剖析“一法多用”的題型,看透問題的本質,找到問題的關聯點,利用所學知識,從“萬變”中也要能夠學會“不變”的思維模式,不斷地進行探索與總結,這樣才能最大程度地理解并且掌握到“變式教學”的巧妙之處。
總之,教師在教學實踐中要深入剖析“變式教學”,使學生掌握學習數學的多種方法,開闊學生的思維境界。“變式教學”的方法多種多樣,本文只是例舉了部分,還有更多的方法值得教師去探索、去發現,將其巧妙地穿插于教學過程中,使學生的數學解題能力更上一層樓。

