A note to some identities are proved by Jacobian identity

Fengjiao LYU

（College of Mathematics Science，Chongqing Normal University，Chongqing 401331，China）

A note to some identities are proved by Jacobian identity

Fengjiao LYU

（College of Mathematics Science，Chongqing Normal University，Chongqing 401331，China）

Two infinite product identities involving sextuple product identity and celebrated Jacobi triple product identity，first derived by John A.Ewell in his thesis，is the Jacobian theory ofθfunctions of this note.These two identities，including one that implies Jacobi’s identity，are proved to be different from John A.Ewell’s method.This article combines the functional equation means and some analytically technique to prove these equations.And a corollary is consequently derived.

infinite product identity；θfunctions；Jacobi’s identity；sextuple product identity introduction

To proof the main results，we need some well-known results.For convenience，we first give out a identity theorem，ones can seen in page 1287of［1］，where author expressed the following sextuple product identity.

Theorem1［1］For each triple of complex numbersa，b，xwith a≠0，b≠0and x ＜1，then

In late 1995，Ewell［1］discovered a sextuple product identity，it is not only pretty shape but also have funny applications in the from of congruence of partition function（see［2－3］）.From the paper［4］，we can seen the various testified means and applications.In addition，in［3－5］we found that all the proof in these papers demand the Jacobi triple product identity and the sextuple product identity.The Jacobi triple product identity is a celebrated consequence，due to Gauss and Jacobi.And the sextuple product identity，due to Ewell，as shown in［1］.

In 1997，Ewell［2］proved an identity represented and being used by Ramanujan in his today classic research of certain arithmetical functions.In fact，the Jacobi triple product identity in one of the simplest and the most significant identities are vintage and crucial objects of study.It will be entertaining to derive some helpful theta function identities.In 1998，Ewell［5］derived eight-fold infinite products，namely Jacobi’s identity.In order to certify Jacobi’s identity，Ewell used an identity first proved by Jacobi in his theory of theta functions.

In 2002，Ewell［3］testified two further results of arithmetical interest.The objective of present paper is to conform all the equations just alluded to a individual formula.Depend on the functional identity method and Jacobi triple product identity，we derived primary theorem.The staple theorem and it’s proof will be given in section 2.

1 Preliminary

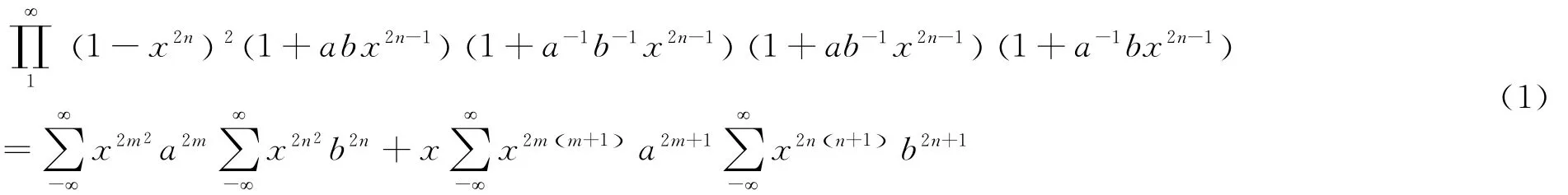
The author proved the theorem 1.His proof is indicated on the celebrated Gauss-Jacobi triple product identity：

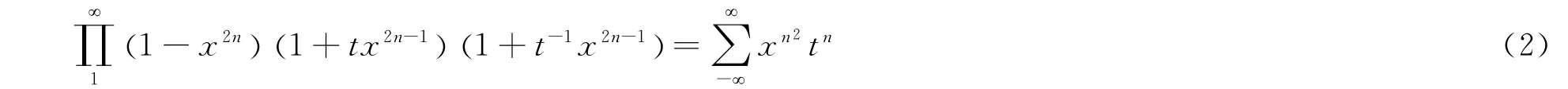
Which is effective for each pair of complex numbers t，xsuch that t≠0and x＜1.

2 Main Results and Proofs

Take these applications intoconsideration，as far as possible other people，it appears reasonably that the fundamental proof of these identities ought to be put forward.So we suggest to do in the present note.Details are given in this segment.In this section，we will give out the main results of this article.And then use the functional equation way and the analytically skill proved it.In other words，by mainly combining the function identities with Jacobi triple product identity，we prove the following result.

Theorem2 For each complex numberxand x ＜1，then

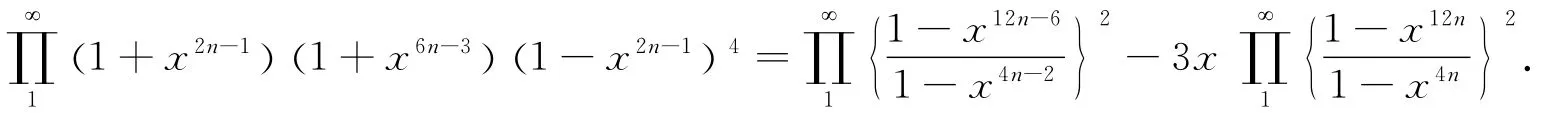
Proof We know that author first use identity（2）to show each series on the right side of identity（1）as an infinite product.

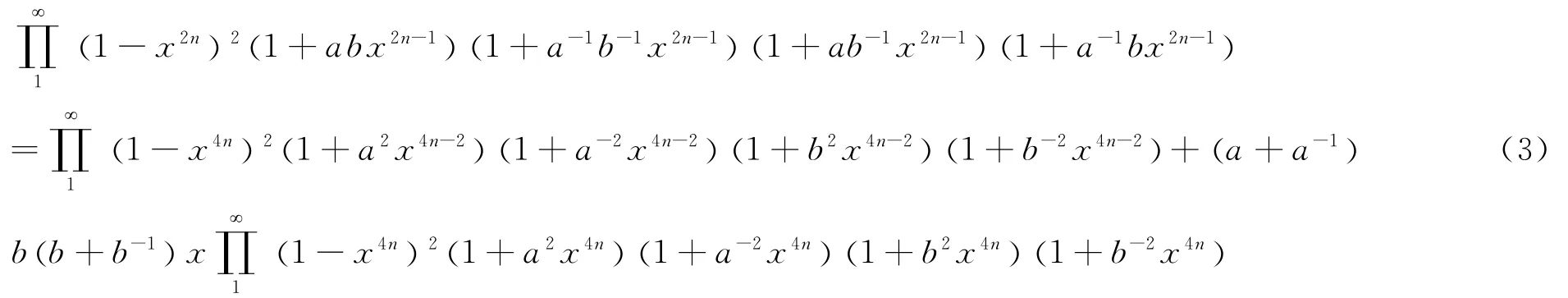
In（3），we let a＝bto have

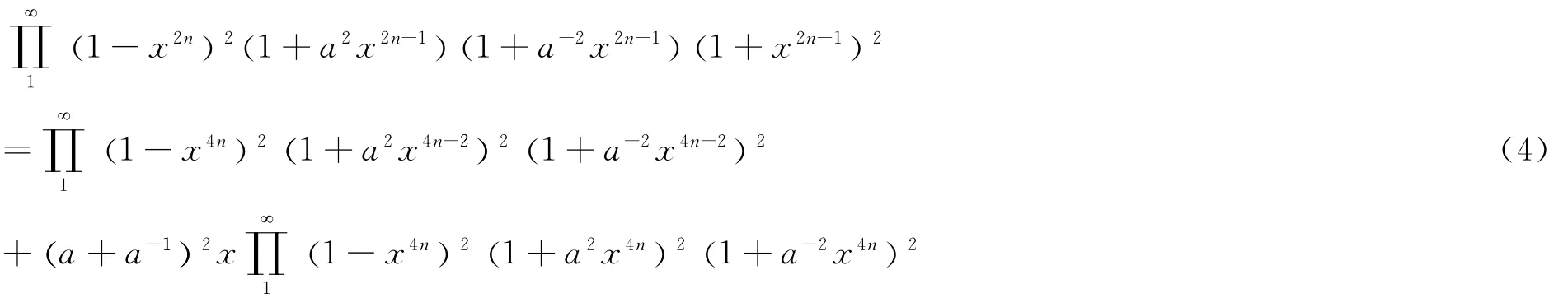
And a→iato get

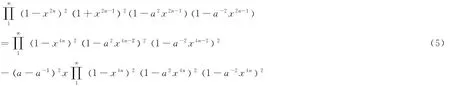
then to get

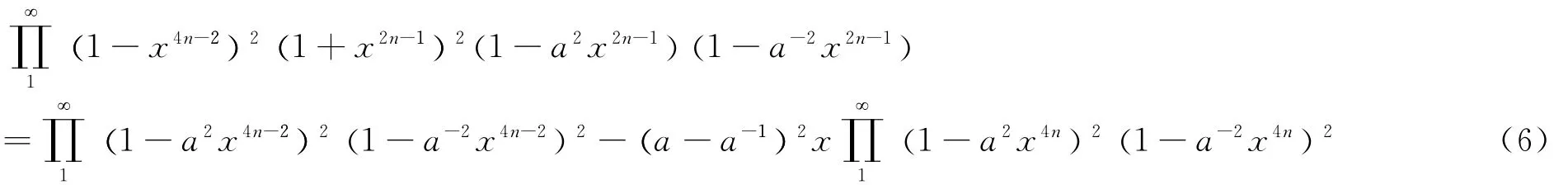
In（6），we then let a→ρto get

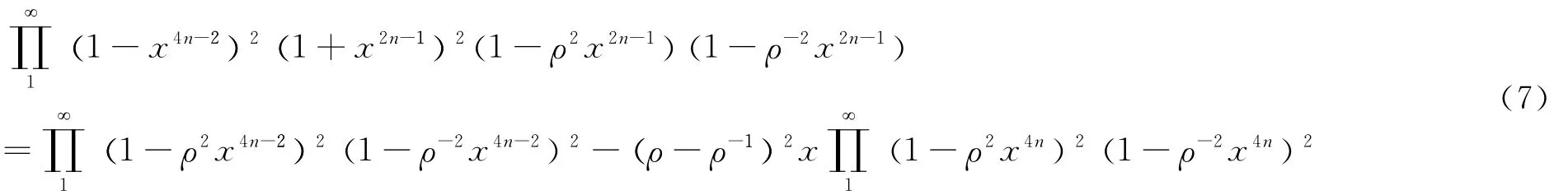
And simplify this identity by make use of the following three identities.The first equation：

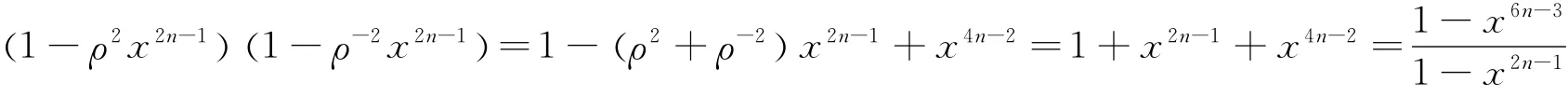
The second equation：

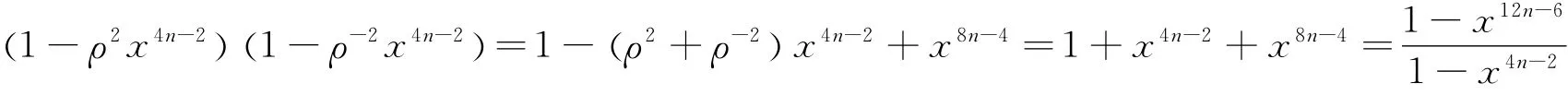
The third equation：

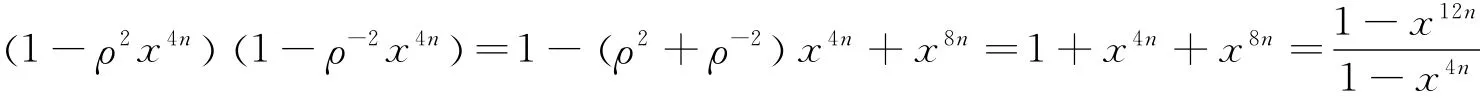
Bring these three equations into（7）to obtain

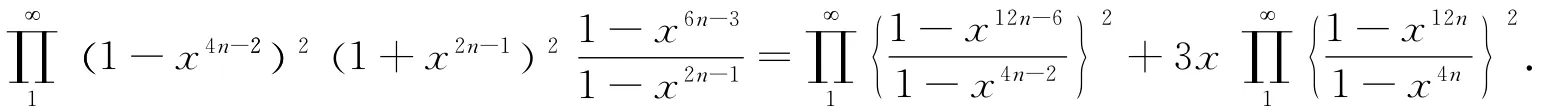
Then we simplify this identity by use （1－x4n－2）2＝（1－x2n－11）2（1＋x2n－1）2to have

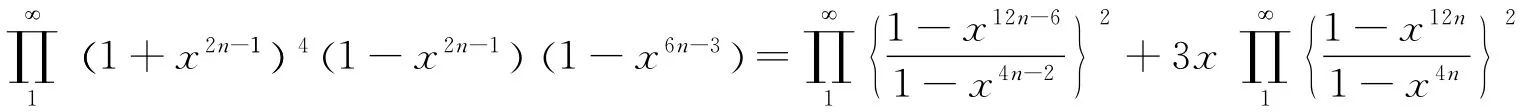
Finally，in the foregoing identity，let x→－x，then the theorem 2follows.

In fact，according the above theorem we can obtain a corollary as following.

Corollary 1 For each complex number x，

Proof In（4），we let a→ia2to get

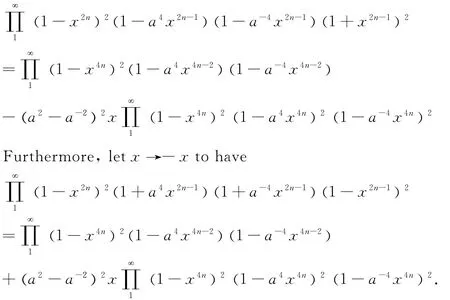
And multiply the foregoing identity and（7）to obtain

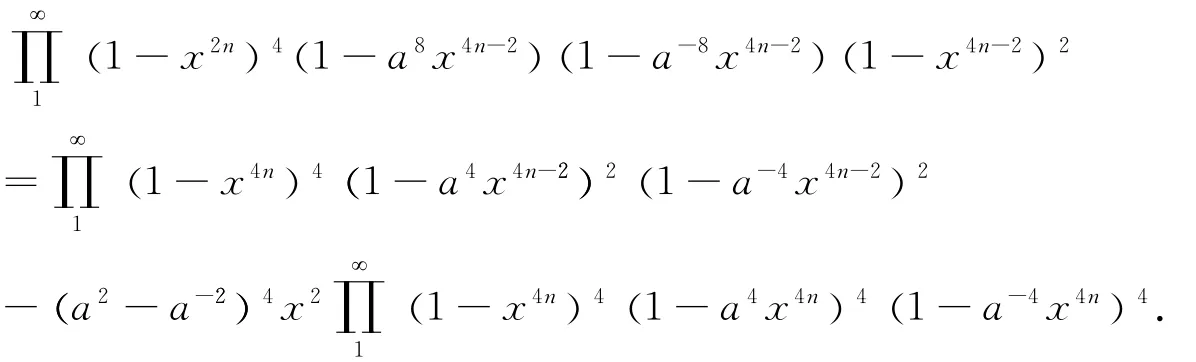
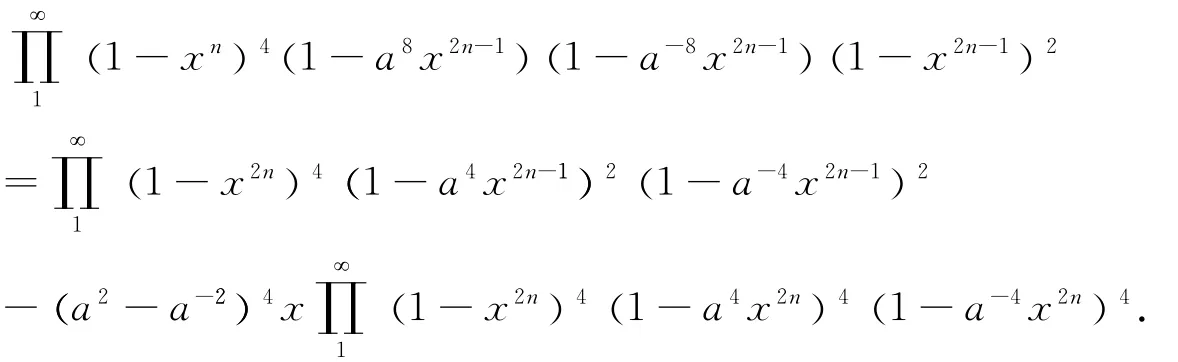
The rest result of this paper is the identity of the following theorem.Of course，Our proof is based on the celebrated Jacobi triple product identity and the sextuple product identity.

Theorem3 For each complex number xand x ＜1，then.we obtain the desired result.

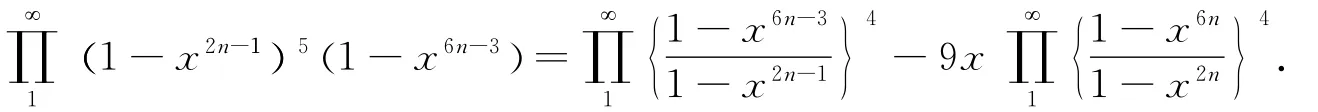
Proof In（6），we let x→－xto have

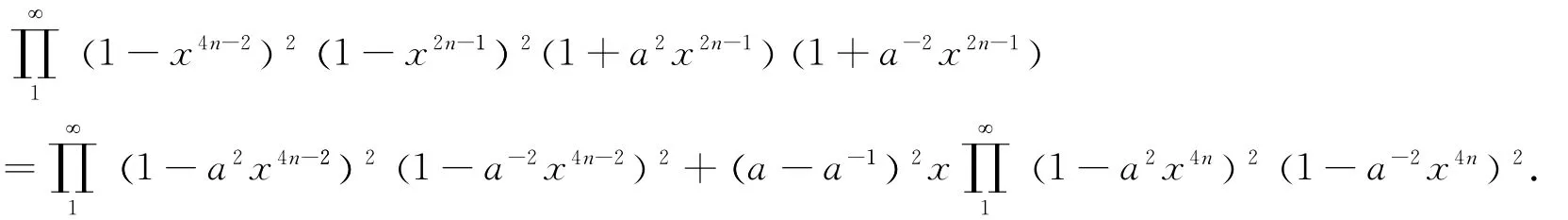
And multiply the resulting identity and（6）to get

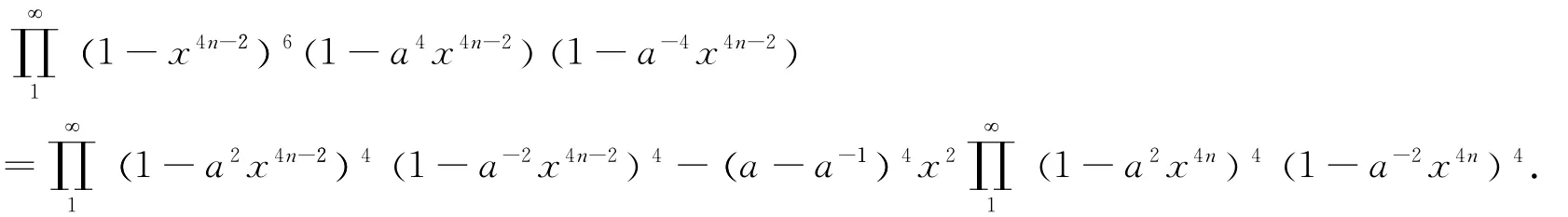
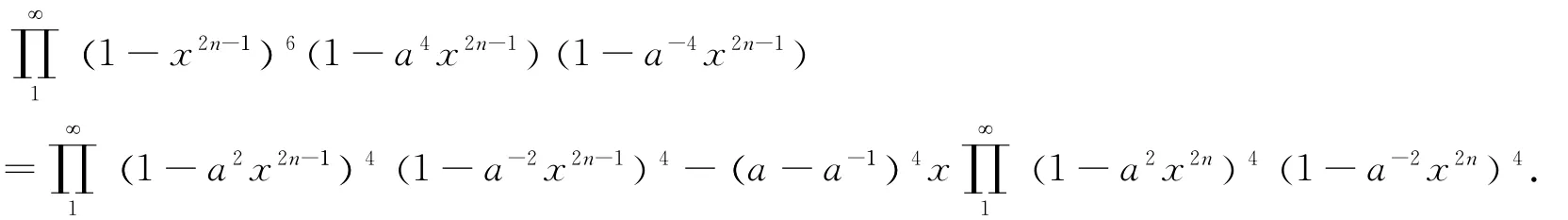
Finally，in the foregoing identity let a→ρto have

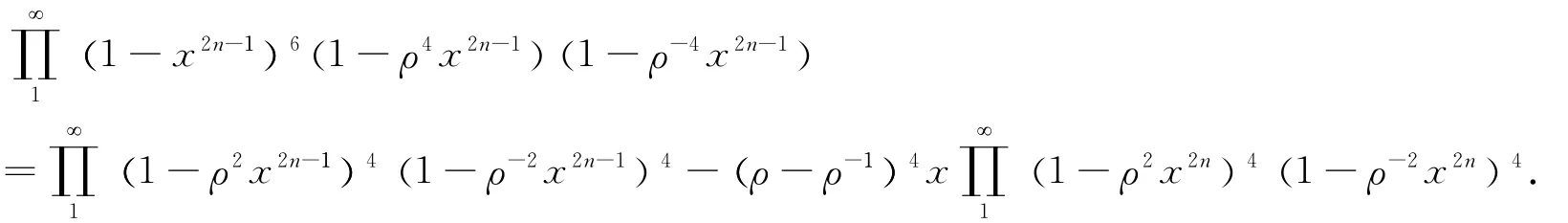
And simplify the foregoing identity by appeal to the following three identities.The first equation：

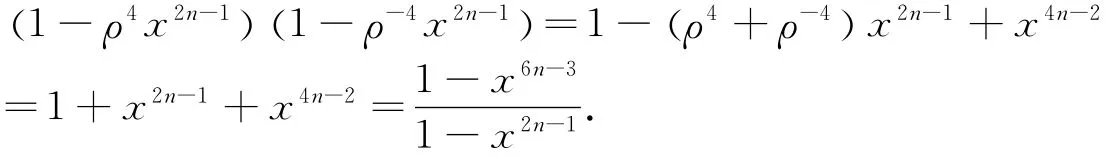
Of course，we know the second equation：

The third equation：

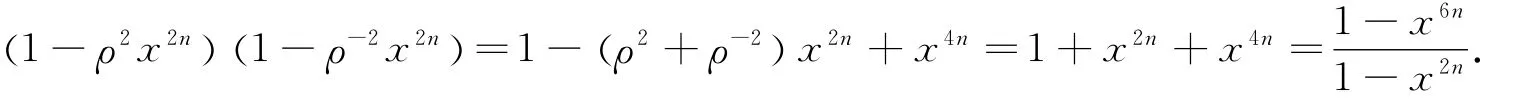
Finally，and simplify to prove identity.We can obtain what we want.

3 Conclusion

It is clear that there are many identities associated with the theory of theta functions.In this paper we have proofs twoinfinite product identities by using the well－known Jacobi triple product identity and sextuple product identity.By uniting the functional equation method and the analytically skill，we derived these result.On the other hand，comparing to John A.Ewell，we propose a method which is different from John to re prove these two identities，and the method is more concise.

［1］J.A.Ewell，Arithmetical consequences of a sextuple product identity［J］.Rocky Mountain J.Math，1995，25（4）：1287－1293.

［2］J.A.Ewell，On an identity of Ramanujan［J］.Proceedings of the American Mathematical Society，1997，125（12）：3769－3771.

［3］J.A.Ewell，Further consequences of a sextuple product identity［J］.Rocky Mountain J.Math，2002，32（1）：123－128.

［4］J.A.Ewell，An easy proof of the triple－product identity［J］.Proceedings of the American Mathematical Society，1981，88（4）：270－272.

［5］J.A.Ewell，A note on a Jacobian identity［J］.Proceedings of the American Mathematical Society，1998，126（2）：421－423.

O175.9 Document code：A Article ID：1671-9476（2017）02-0020-04

10.13450／j.cnkij.zknu.2017.02.005

2016-09-18；Accepted：2016-10-16

Biography：LYU Fengjiao（1990－），female，Nanchong，Sichuan，postgraduate，research direction：special function.