基于阿克曼原理的舵機與差速電機協同控制算法的研究與應用

周潤發，楊 琦，汪元禮，李 丹，衛軍帥

（1.安徽工業大學 電氣與信息工程學院；2.安徽工業大學 工程實踐與創新教育中心；3.安徽工業大學 學生工作部，安徽 馬鞍山 243002）

基于阿克曼原理的舵機與差速電機協同控制算法的研究與應用

周潤發1，楊 琦2，汪元禮1，李 丹1，衛軍帥3

（1.安徽工業大學 電氣與信息工程學院；2.安徽工業大學 工程實踐與創新教育中心；3.安徽工業大學 學生工作部，安徽 馬鞍山 243002）

本文依據阿克曼原理分析了智能車C車模轉彎時前軸舵機角度與后軸電機差速之間的關系，提出了提出改進式的PID控制伺服舵機轉角與雙電機差速協同控制的優化算法，通過智能車在轉彎時速度和穩定性的實驗數據驗證了該算法正確性.

阿克曼原理；差速控制；PID控制

隨著最些年來汽車工業不斷發展和自動控制技術的不斷升級，智能汽車特別是無人駕駛汽車是發展的重要方向之一，如何使智能汽車高效、穩定地運行，特別是轉彎過程成為大家爭相研究的課題.本文依據阿克曼原理，對恩智浦智能C車模轉彎時前輪的轉向與后輪差速的協同配合進行研究，提出改進的PID控制算法，使車模能夠更好地轉向.

1 理論模型

阿克曼原理是在不考慮汽車質心側偏、汽車行駛過程中的側向力、橫擺角和極端惡劣的路況下，車輛無論是直行還是在拐彎時，如果每個車輪的運動軌跡都可以完全符合它的自然運動軌跡，那么就可以保證輪胎與地面間處于純滾動而無滑移現象.兩軸車在轉向行駛過程中，全部車輪須繞一個瞬時中心點（轉向中心）做圓周滾動，而且前內輪與前外輪的轉角應滿足一定的關系，這樣才可以保證輪胎與地面間處于純滾動而無滑移現象，從而保證車輛在行駛時是相對可控的.

恩智浦智能車競賽中的C型車模的二軸車機械結構決定了后軸兩輪與轉向中心在一條直線上，由于后軸兩輪距離與阿克曼原理的轉向中心的距離不等，所以只有在一段很短的時間內左右兩輪的轉速不同，才能繞一個轉向中心做圓周滾動,進而有效地保證整車的穩定性.

我們可以借助單片機高頻特性對整車的運動狀態進行分析，在每個微分時間段內，不斷地通過前軸舵機角度和對輸出PMW波對后軸電機之間的轉速進行調整，保證整車的配合，從而使車輛滿足阿克曼原理，進而保證輪胎與地面間處于純滾動而無滑移，使之過彎平穩，過程可控.

2 數學模型

2.1 后輪兩輪的差速關系

根據阿克曼轉向的幾何要求，恩智浦智能車C型車模所全部車輪就都必須繞一個轉向中心點做圓周滾動，如圖1所示，其中W為后輪兩輪的輪距，L為前后輪的間距，以及如圖示的各點與轉向中心的角度，入彎之后的車模后輪里面的轉速為V_in，入彎之后后輪外面的轉速為V_out.

根據物體的圓周運動規律公式V=ω×R，由于單片機的一個工作周期相對于整個運動過程非常短，設單片機的一個完整工作周期時長為dt，那么ω=dθ/dt，則導出速度公式V=dθ×R/dt.而且，R_in=R-W/2,R_out=R+W/2，如圖2所示，根據阿克曼原理，車輛的后輪必須繞同一個轉向中心做圓周滾動得知，此時就要滿足那么后面兩個輪子的角速度是相同，即可以推導出

內輪產生的移動dx_in=R_in×dθ/2π，外輪產生的偏移 dx_out=R_out×dθ/2π， 由 于 V_in= dx_in/dt, V_out=dx_out/dt，進而推導出過彎時的差速公式：

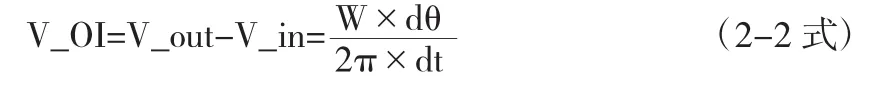
其中的W為常量，dt為常量是單片機完整工作一個周期的時間.為進一步分析dθ與理想位置（中線）的關系，改進PID控制算法，下面我們對dθ進行的探討.

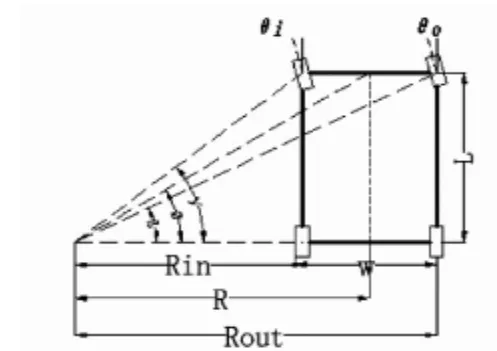
圖1

圖2

2.2 過彎的曲率與改變的角度dθ的關系

賽道提取算法是：車模上的傳感器（攝像頭）從車的近處向遠處掃描合理的區間內跳變點（即邊沿追蹤濾波算法），并將每一行的跳變點存入一個數組，因為車處于賽道之上，我們可以找到多行跳變點，不會出現完全丟線的情況.我們利用Δt時刻采集到的跳變點y1、y2，與Δ(t+1)時刻的跳變點y1'、y2'進行分析處理.利用斜率公式：tanθ=(y2-y1)/ (x2-x1)=Δy/Δx.其中Δx相當于傳感器（攝像頭）當前采集行行距D，y為跳變點的坐標位置.抽象出的賽道信息如圖3所示.

其中K為曲率，ds為微分弧長，dθ為偏移角度，dx在圖3中的體現為豎直方向的增加量.

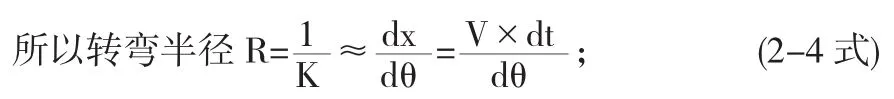
dθ如圖3標注所示，為y1與y1'相對于中心的偏移角度，也近似是直線y1y2與直線y1'y2'交線的夾角，由于在角度很小時存在tan（θ）≈θ，即可以得出

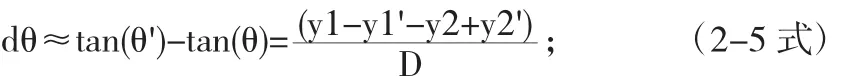
我們帶入上面的（2-2式），得到差速方程

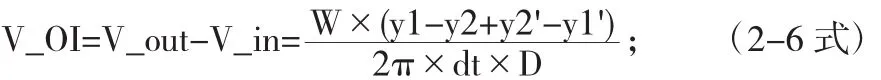
圖3

圖4

2.3 將差速進行自適應分配

為將差速分配給兩邊電機，我們設外輪轉速V_out= V+A×V_OI，內輪轉速V_in=V-(1-A)×V_OI，其中V為速度設定值,A為差速自適應分配比例因子，由2-1式，得

結合(2-4式)，（2-5式）與（2-6式），我們可以看出差速自適應分配比例因子主要由dθ所決定.而式中的(y1-y2)就是傳感器（攝像頭）在一個時刻從賽道提取出的路徑誤差，那么(y1-y2+y2'-y1')也就是經過dt后，同行路徑誤差之差.我們將其作為對系統輸出誤差的反饋，通過反饋來調整差速自適應分配比例因子以及差速大小，從而達到A可以通過誤差參數dθ進行自我調整.

2.4 舵機與差速的協同配合

通過舵機打角與電機差速的配合，從而保證舵機所打角度的轉向中心與電機差速的轉向中心一致，控制舵機轉角的PID控制程序為

其中J_angle為舵機所打的角度，P、I、D為PID控制的調整參數，ER_all為誤差的累積.

3 實驗數據及其分析

我們選取飛思卡爾K60單片機作為車模的控制核心，傳感器采用攝像頭OV7725，歐姆龍系列200P/R編碼器對兩邊電機測速，對電機轉速進行了閉環控制，并通過藍牙模塊將車輛在賽道中的位置情況實時傳輸給上位機.

車模電機主要技術參數如下：額定工作電壓7.2V；最大工作電壓9.6V；最大效率點：電流0.679A、轉速13050轉；最大功率點：電流1.537A、轉速8044轉；堵轉電流2.916A，馬達到后輪的傳動比為7.46.

測試賽道環境：賽道路面采用專用白色PVC耐磨塑膠基板制作.跑道表面為白色，賽道兩邊有黑色線，黑線寬25mm±5，沿著賽道邊緣粘貼，賽道寬度為45cm.（賽道中間坐標位置我們設為40），如圖4所示.

車輛過彎偏移賽道的數據記錄如下：如圖5所示的是差速控制時車模偏移賽道中線情況曲線，如圖6所示的是無差速控制時車模偏移賽道中線情況曲線，我們可以從圖中看出，在無差速控制時車模偏移賽道中線的范圍在21—68之間，在差速控制時車模偏移賽道中線的范圍在28—58之間，由此看出，在差速控制算法下車模偏移賽道理想中線的最大位置有較大幅度減小，增強了車模過彎的穩定性，與此同時，車模從偏移到回正的時間也將相應減少.我們測量車速時也發現，未加差速控制時車模過彎速度平均為1.9m/s，加入差速控制后平均車速提升為2.3m/s，速度提升超過20%.

圖5

圖6

由此可見采用基于阿克曼原理的舵機與差速電機協同控制算法能夠使過彎性能得到明顯提升.

4 結果與結論

通過將阿克曼轉向原理運用于C車車模過彎過程分析，在單片機控制C車模時的應用進行推導，提出差速分配比例因子，得出微分情況下阿克曼轉向原理的改進式PID控制伺服舵機轉角與雙電機差速控制的優化算法，使舵機打角的阿克曼轉向中心與電機差速的轉向中心相一致，從而在車模過彎過程舵機打角與電機差速更好地配合，對改進智能車的過彎性能以及現代電動汽車的發展研究具有實際意義.

〔1〕卓晴，黃開勝.學做智能車[M].北京：北京航空航天出版社,2007.3.

〔2〕李科澆,赫玉瑩，范恒超.后輪雙電機差速與前輪轉向協調控制在智能車模上的應用[J].科學與財富,2014(4)：46-47.

〔3〕姜明國,陸波.阿克曼原理與矩形化轉向梯形設計[J].汽車技術,1994(5)：16-19.

〔4〕楊其華,張乃標.雙電機獨立驅動電動汽車的電子差速自調節功能的分析研究[J].北京汽車,2008(5)：28-37.

〔5〕許曉飛,夏培容.智能車速度的模糊控制最優循跡策略研究[J].北京信息科技大學學報(自然科學版),2009,24(3): 85-86.

TP273

A

1673-260X（2017）07-0014-02

2017-04-18

安徽省大學生創新創業訓練計劃項目（201610360340）；安徽省大學生創業實驗室建設計劃項目（2015ckjh010）；安徽省思想政治教育改革計劃項目（szzgjh1-2-2016-5）；安徽工業大學校企合作實踐教育基地項目(2012-5)