關注過程，提升實效

解祥峰

[摘 要] 隨著新課程改革的深化，“過程與方法”作為增補的一個維度的教學目標讓我們教師越來越多地意識到“學習過程”的重要性，關注學生的學習過程能夠切實提升學生的數學核心素養，關注需要我們教師在問題的設計上更用心，需要我們對學生解題的過程和結果有統計與分析.

[關鍵詞] 高中數學；過程與方法；問題

新課程提出了三維教學目標，“過程與方法”是其中的一個維度，關注學生的學習過程是落實學生是學習的主體這一理念的重要保障，同時也意味著我們教師在教學過程中要改變傳統的灌輸式的數學教學方法，把引導學生的主動學習和探討作為教學活動的中心環節，唯有如此才能有效達成過程與方法目標，對于高中數學學科教學而言如何做到關注學生的學習過程呢？筆者認為需要我們教師精心設計問題，需要對學生的問題解決過程有足夠的關注，需要有足夠的耐心引導學生從思維障礙中走出.

[?] 課前情境的設計，引導學生自主加工和處理信息

對學生學習過程的關注應該從課前的自主預學開始，預學的過程是學生將原有知識和經驗作為資源進行信息加工和處理的過程，無論是新授課還是復習課，都應該引導學生高質量地完成這個過程. 對于高中數學這門學科，我們在情境的設計上應該盡可能地做到形象化、直觀化，這樣有利于信息的調取.

例如，“橢圓的方程復習”筆者設置了如下兩個情境，引導學生在課前進行信息加工和處理.

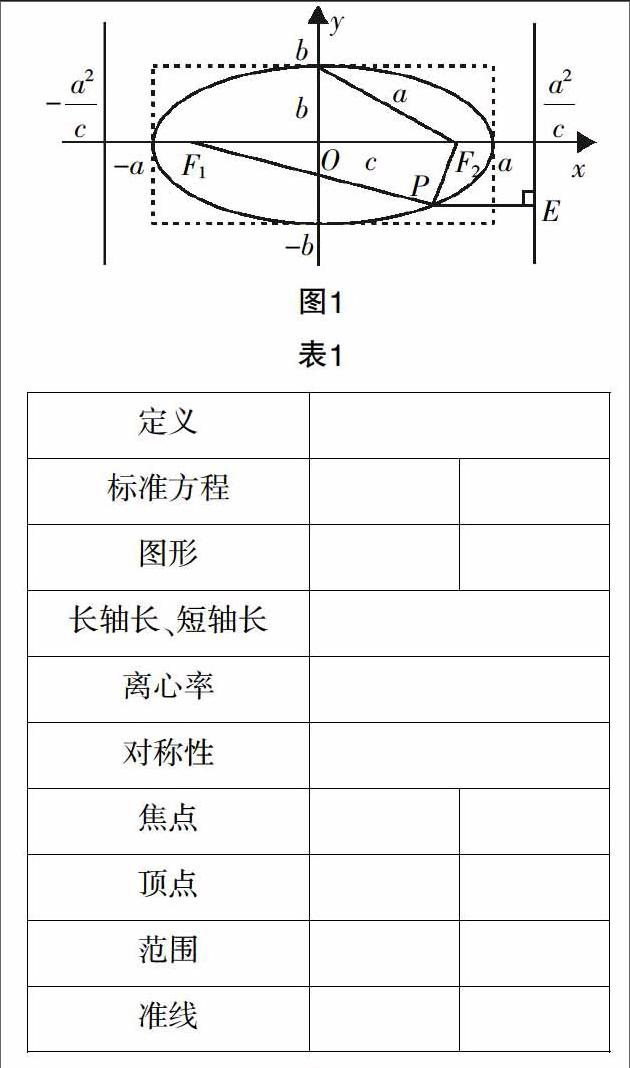
情境1：說說和橢圓相關的知識有哪些？并根據你所了解的知識填寫表格.

設計意圖：這樣的設計有助于“過程與方法”目標的達成，首先借助于圖1，學生在圖像直觀的帶領下，思維發散完成形到數的轉化，把幾何關系轉化為代數關系的思維過程，再借助于表格，引導學生對所學知識進行及時的回顧和總結，有利于學生充分掌握知識，厘清關系，為應用知識奠定基礎.

[?] 課內設計問題串，幫助體驗思維的過程

傳統的教學模式下，教學目標是單維度的，就是教給學生知識，考試似乎成為對學生知識面和方法面的考查. 隨著課程改革的深化，我們越來越多地認識到學生思維過程的重要性，而思維過程是不可灌輸的，我們在平時的課堂教學過程中如何幫助學生體驗思維的過程呢？筆者認為可以通過問題串的設置幫助學生體驗思維的過程，深化對數學概念的本質的認識.

下面以“函數單調性”重難點的突破為例，筆者設計了如下的問題串，幫助學生深入理解“任意”二字的含義.

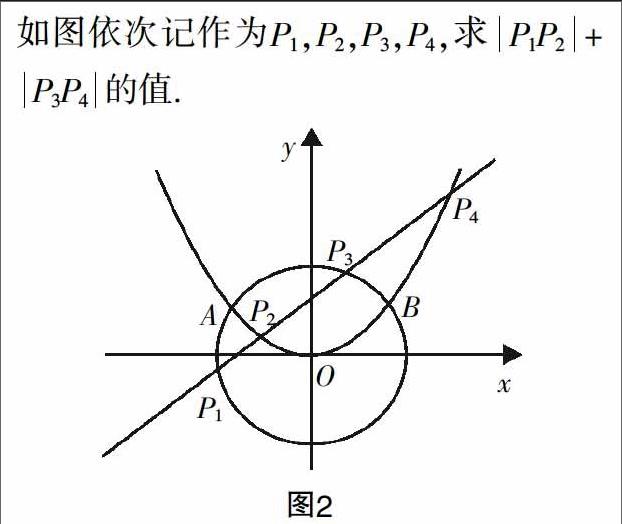
問題1：對于函數f（x）=x2，如果有f（-1）

問題2：對于函數f（x）=x2，如果有f（1）

問題3：x1，x2是區間[0，+∞）上任意的兩個數，如果x1

設計意圖：“函數單調性”定義的表述中“任意兩個”是經常用到的字眼，學生面對這樣的表述必然經常是心有疑慮的，因此，教師在教學中要引導學生感知“任意兩個”這種數學語言表達的重要性和必要性，激發學生的對比和思考，而且，“如何想到從任意兩點的變化方向這個角度來研究該函數屬于單調遞增函數還是單調遞減函數”正是教學的難點，也是“用局部點的性質刻畫整體性質”這一數學領域中經常用到的方法. 函數單調性的定義，要求對任意的x1、x2都要成立，即取遍所有的變量x. 學生的思維基礎在哪里？如果僅僅是采用反證法，“若命題不成立，則要舉反例來說明”，那么，學生的思維是沒有得到發展的. 處于這樣的思考，筆者在教學中進行了上面問題的設計，通過問題的設置，將“單調性概念”的理解具體化、形式化，這也是學生在分析解決問題的過程中必須解決的一個環節. 為了使學生的理解能力能夠突破題意，教師在教學過程中設置了一系列的問題，有針對性地引導啟發學生的思考和學習，達到教學的初衷和目的.

當然，對于高一的學生而言，其思維能力和理解能力是有限的，也是參差不齊的，在一節課的教學中，要達成學生對于某一個具體的概念（如上面的函數單調性）有深入理解是不可能的，學生對概念的理解也是有一個過程的. 因此，教師在教學中，要先從直觀的表述或者畫圖開始，使學生先建立對概念表象的初步認知，然后把學生的認知層面逐步提高上升至深度理解的理性層面，把圍繞核心問題設置的疑問鏈精心地思考設計好，并且根據學生各個階段的學習狀況恰如其分地穿插進問題設計的環節，使學生對數學原理理解得更為深刻，在體驗思考并解決問題的過程中使學生的思維能夠得到有序的發展與提升.

[?] 課外統計與調研學生解決問題的過程，引領學生走出困惑

對學生學習過程的關注不僅僅在課堂內，還應該延伸到課堂之外，尤其是對學生作業完成情況的過程性評價與分析. 很長一段時間，我們對待學生課后作業完成情況都是采用的結果性評價，即統計有多少人做錯了，錯的人多就上課統一講評一下正確的做法，如果錯的人不多則在作業本上用紅筆寫上大大的“訂正”二字. 這樣的處理方式有對學生學情的了解，但是缺乏對學生思維過程的調研，不利于過程與方法教學目標的達成，實踐經驗表明，教師不能僅僅憑借于學生對于問題解答的最后結果，尤其是關注學生解題過程中出現了怎樣的錯誤，反思學生出現錯誤的根源在哪里，是知識障礙，還是思維障礙，在講評的過程中要展示學生的錯誤，引導學生以學習小組為單位，分析錯在哪里，同時有針對性地引導學生自己歸納小結、反思與糾錯，使得學生在這個過程中提升自身的認知與探究能力. 下面就以一個具體的作業題進行分析.

作業：如圖2所示，點A與點B是圓x2+y2=12和拋物線x2=4y的兩個交點，其中，拋物線的焦點記作為F，有一條直線l經過點F且其斜率是1，該直線分別與圓和拋物線相交，且有四個不一樣的交點，

學生作業完成過程調研：學生作業完成的過程反映了他對于知識點掌握的情況，以及他在實際解答的過程中思維的方向，筆者可以掌握學生的學情，從學情出發，筆者再和學生一起進行探究、反思和糾錯，一般來說，學生作答有以下幾種情形.

情形1：對于知識點的掌握無法貫通，以致思維一團混亂，無法解答；

情形2：對于P1，P2，P3，P4的坐標基本能夠嘗試解出，但是無法進行下一步的作答；

有針對性地組織講評：對于學生解題大致會出現的情況有了一定的了解后，筆者注意找出學生錯誤的原因，并且在題目講評時，在學生錯誤的關鍵點上進行引導和點撥，啟發學生首先獨立思考，反思自己解題中的薄弱點，再一次分析與嘗試，試著找準解決問題的方向，提升自己的思維能力和解決問題的能力，當然也有可能再一次嘗試后，有部分學生還是找不到正確的解題思路，怎么辦？在學生獨立思考的基礎上，將學生作業暴露出來的錯誤的情形投影到大屏幕上，以學習小組為單位，大家來找茬，這樣的做法不僅僅關注了學生作業完成的過程，還豐富了學生從困惑中走出來的過程，學生對數學概念的印象和理解會更加的深刻.

總之，在教學改革日趨深入的當下，我們教師應該意識到知識的傳授只是新課程標準中教學目標的一個方面，對于高中數學來說，“過程與方法”相對其而言是重要的教學目標，關注“過程與方法”目標的達成是培養學生數學能力和素養的重要抓手，也是順應新的課程理念改變課堂教學模式的必然產物.不僅如此，大量高中數學教學實踐的經驗表明，“過程與方法”教學目標的達成能夠深化學生對知識的理解與掌握，即能夠助推知識與技能目標的達成；同時學生經歷了過程的體驗，對數學學習的興趣變濃了，解決困難的意志變強了，即能夠幫助學生形成正確的情感、態度和價值觀.