變速運轉球軸承保持架的動態性能仿真分析
屈馳飛,楊震,謝鵬飛,張致遠,李超強
(1. 洛陽軸研科技股份有限公司,河南 洛陽 471039; 2. 河南科技大學 機電工程學院,河南 洛陽 471003;3.北京控制工程研究所,北京 100094)
某型號特種電動機采用一對角接觸球軸承作為旋轉支承,該電動機在工作時需反復進行加速、減速或過零運轉,與勻速運轉相比,該工況下軸承的運轉狀態更加惡劣,保持架的動態性能更加復雜。為研究變速運轉下保持架的動態性能,利用動力學仿真軟件建立了變速運轉軸承仿真分析模型,對比分析了變速運轉和勻速運轉軸承的保持架動態特性。
1 仿真分析模型及求解
1.1 數學模型
1.1.1 保持架與鋼球的作用力
保持架兜孔與鋼球的法向作用力為[1-2]
(1)
Cp=0.5(Dp-Dw),
k=1.033 9(Rη/Rξ)0.636,
R=RξRη/(Rξ+Rη),
Rξ=0.5DwDp/(Dp-Dw),
Rη=0.5Dw,
ε=1.000 3+0.596 8Rξ/Rη,
Γ=1.527 7+0.602 3ln(Rη/Rξ),
式中:Kc為試驗數據確定的線性逼近常數,對于球軸承,Kc=11/Cp;zcj為第j個兜孔中心相對于孔內鋼球中心的位移;Cp為保持架兜孔間隙;Dp為保持架兜孔名義直徑;Dw為鋼球直徑;Kn為鋼球與保持架兜孔接觸處的載荷-變形常數。
1.1.2 保持架-引導套圈的作用力
由于流體動壓效應的存在,引導套圈與保持架之間會產生相互作用力及力矩,根據保持架與引導套圈的幾何關系,套圈引導表面與保持架定心表面可以看成是有限短的厚膜作用軸頸軸承的一個特例,如圖1所示。圖中:局部坐標系Sc={Oc,yc,zc}為保持架坐標系,yc軸為保持架中心與最小油膜厚度h0所在點的連線,與全局坐標y軸的夾角為ψc。保持架外圈引導時,ψc=ψ'c;內圈引導時,ψc=ψ'c+π。由油膜分布壓力產生的合力Fc可用2個正交分量F'cy和F'cz來表示,產生的摩擦力矩用M'cx來表示[1-2]。F'cy,F'cz,M'cx分別為
(2)
(3)
(4)
λ=e/C1,u1=R1(ω1(2)+ωc),V1=R1(ω1(2)-ωc),
式中:η0為潤滑油的動力黏度;R1為保持架定心表面半徑;L為保持架定心表面寬度;C1為保持架引導間隙;e如圖1中標注;λ為保持架中心相對軸承中心偏移量;u1為潤滑油拖動速度;V1為兩表面相對滑動速度;ω1(2)為軸承外(內)圈角速度;ωc為保持架角速度。
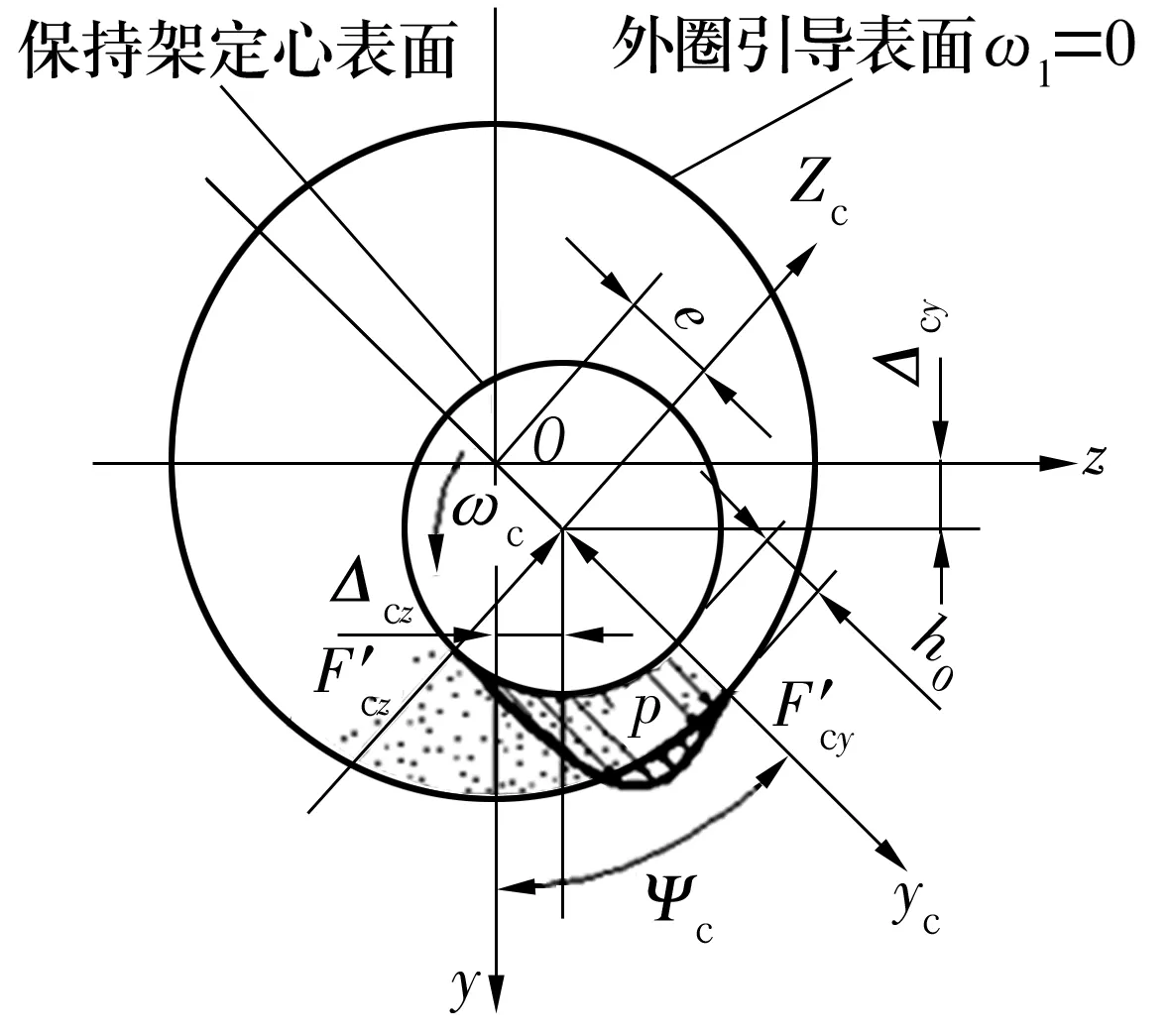
圖1 引導套圈與保持架的接觸關系Fig.1 Contact relationship between guide ring and cage
F'cy,F'cz和M'cx是在保持架坐標系Sc中度量,在建立保持架平衡方程時,需將這些力以及力矩投影到軸承靜坐標系中,即
(5)
ψc=arctan(Δcz/Δcy),
式中:ψc,Δcz,Δcy見圖1。
1.2 求解過程
利用ADAMS系統CMD語言開發了參數化變速球軸承保持架動態仿真分析模型[3-5],基于數學模型以及鋼球與套圈的相互作用模型,用FORTRAN語言編寫軸承零件相互作用力子程序,并編譯生成動態鏈接庫文件與ADAMS求解器模塊連接。FORTRAN程序通過調用功能子程序SYSARY讀取ADAMS中每個時間步長的系統狀態值,計算出初始解,再通過數組RESULT傳遞給ADAMS求解器,完成每個步長的積分求解。
2 仿真結果
利用建立的軸承仿真模型,以某型號軸承為例進行仿真分析,軸承主要結構參數見表1。主要分析軸承在勻速和變速2種工況下的動態性能,軸承勻速運轉轉速為3 500 r/min,變速運轉軸承轉速曲線如圖2所示。

表1 結構參數Tab.1 Structural parameters
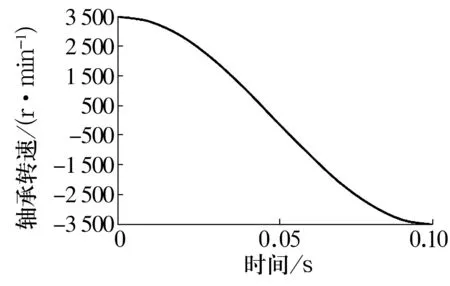
圖2 轉速曲線Fig.2 Speed curve
仿真分析軸承在0.1 s內的動態性能,分10 000步進行計算,在仿真開始時首先給鋼球和保持架設定一個初速度,在仿真計算約0.002 s(計算步長為200)后,鋼球與保持架的轉速趨于穩定。
2.1 保持架受力分析
保持架主要受保持架與鋼球的作用力和保持架與引導套圈的作用力。勻速和變速運轉條件下保持架受力仿真結果如圖3、圖4所示。由圖可以看出,變速運轉軸承的保持架受力均大于勻速運轉軸承,結合圖2可以看出,變速運轉軸承在轉速方向變化后保持架受力突然增大,然后減小,說明保持架與鋼球和引導套圈間出現了劇烈碰撞。

圖3 保持架與鋼球的作用力Fig.3 The force between cage and steel ball
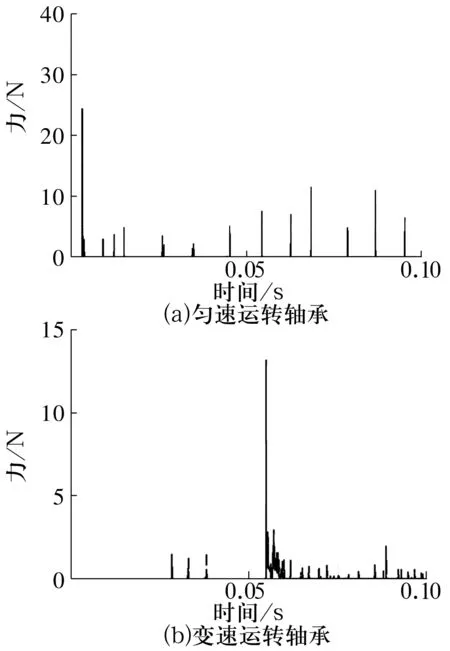
圖4 保持架與引導套圈的作用力Fig.4 The force between cage and guide ring
2.2 保持架打滑率對比分析
軸承保持架打滑率為
(6)
式中:n為保持架實際轉速;ncl為保持架理論轉速。
保持架打滑率反映了保持架實際轉速與理論轉速的差值,打滑率越小,保持架實際轉速與理論轉速越接近,鋼球與溝道間的滾動成分越多,滑動成分越少,由滑動導致的摩擦與磨損越小,越利于保持架運轉穩定;反之,打滑率越大,將給保持架運轉穩定性帶來不利影響。
勻速和變速運轉軸承保持架的打滑率如圖5所示,可以看出:1)勻速運轉時,由于軸承承受軸向和徑向聯合載荷,鋼球在經過徑向承載區時轉速發生變化,從而造成保持架打滑率出現波動,平均打滑率約為2.3%,最大打滑率約為3.3%;2)變速運轉過程中,結合圖2可以看出,在軸承從正轉變為反轉后,保持架打滑率突然增大至61%,這是由于軸承套圈轉速換向過快,套圈溝道對鋼球的拖動力不足,造成鋼球公轉換向相對于套圈出現滯后,鋼球在溝道內出現打滑,從而導致保持架打滑率突然增大。

圖5 保持架打滑率Fig.5 Slipping rate of cage
2.3 保持架質心軌跡分析
保持架質心運動軌跡的發散和平滑程度,可以反映保持架的運轉穩定性,質心軌跡越規則越平滑,說明保持架運轉越穩定;反之,保持架運轉穩定性較差。勻速運轉和變速運轉軸承保持架的質心軌跡如圖6所示,軸承仿真0.1 s,共5.5個速度循環周期。由圖6可以看出,勻速運轉軸承的保持架質心軌跡非常規則,近似為圓形;而變速運轉軸承保持架的質心軌跡比較紊亂,質心有較大的斜向位移,出現了類似菱形的質心軌跡,這說明保持架受到了較大的沖擊力,造成保持架質心位置突然變化。

圖6 保持架質心軌跡Fig.6 Trajectory of cage centroid
3 結論
利用動力學仿真模型實現了變速運轉軸承的仿真分析,通過分析勻速和變速運轉條件下軸承的保持架受力、打滑率以及質心軌跡,得出如下結論:
1)相對于勻速運轉軸承,變速運轉軸承的保持架受到的瞬間碰撞力更大,保持架運轉軌跡相對紊亂;
2)對于變速運轉軸承,在軸承轉速換向后,由于套圈對鋼球的拖動力不足,造成鋼球在溝道內出現了嚴重的打滑現象,從而造成保持架打滑率、保持架與鋼球以及引導套圈的作用力急劇增大。

