例談一類數陣圖的填法

文︳李艷華

例談一類數陣圖的填法

文︳李艷華

數陣圖是一類非常有趣的數學問題，它變化多端，引人入勝，奇妙無窮。許多喜歡探究數字規律的人對數陣圖十分著迷，以至有些人留連其中，用畢生的精力研究它的變化。大數學家歐拉對它都有著濃厚的興趣，數陣圖的魅力由此可見一斑。在給學生講解數陣圖的教學中，筆者嘗試用淺顯易懂的方法，帶學生進行了探究。

諸如下面的數陣圖，要將所給定的數填入圓圈內，使各線上的數字之和相等，我們無需盲目去套，按下面的方法即可輕而易舉地填出。

圖1 填入1～13

圖2 填入1～19

圖3 填入1～25

圖1：由于1+2+3+…+13＝（1+13）×13÷2＝91，91需減去一個奇數才能被2整除，所以交叉處的可填1，3，5，7，9，11，13，共有7種基本填法。

圖2：由于1+2+3+…+19＝（1+19）×19÷2＝190，190需減去1，4，7，10，13，16，19，即減去除以3余1的數才為3的倍數，所以交叉處的可填這7個數，故共有7種基本填法。

圖3：由于1+2+3+…+25＝（1+25）×25÷2＝325，325需減去1，5，9，13，17，21，25，即減去除以4余1的數才為4的倍數，所以交叉處的可填這7個數，故共有7種基本填法。

第二步：按如下順序填入。先填好交叉處的A，再將其他數由小到大按圖以B，C，D，E，F…的順序（似8字形）依次填入即可（如圖4、5、6所示）。

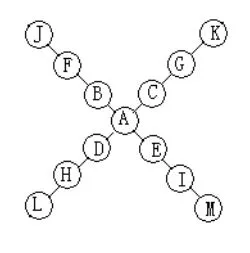
圖4

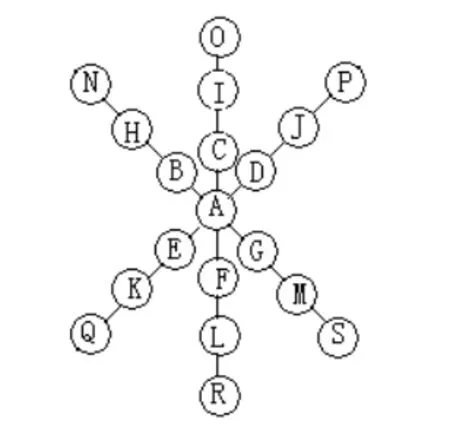
圖5

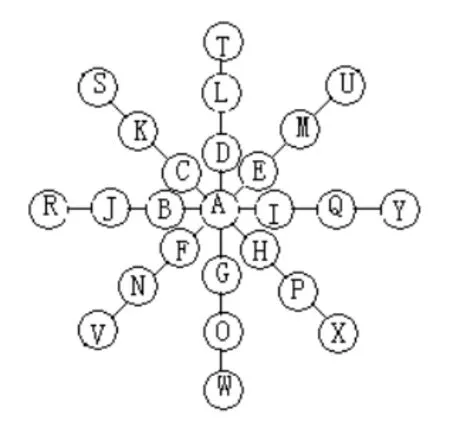
圖6

下面給出圖4、圖5中的A為7，圖6中的A為9時的一種填法（如圖7、8、9所示）。

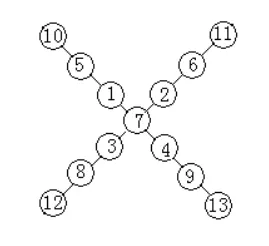
圖7

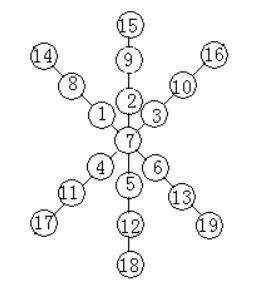
圖8

圖9

對于這類數陣圖，我們還可以得出這樣的規律：基本填法的種數與線上的個數相同。

對于圖3，如要求三個大的圓上的數之和也要相等，我們需將按上法填好的數進行對調。不過此時的基本填法減少了：因為325減去5，9，17，21時不是3的倍數，亦即交叉處的內只能填1，13，25才能使三個圓上的數之和也相等。具體填法較易，下面僅以13為例填之（如圖10所示）。

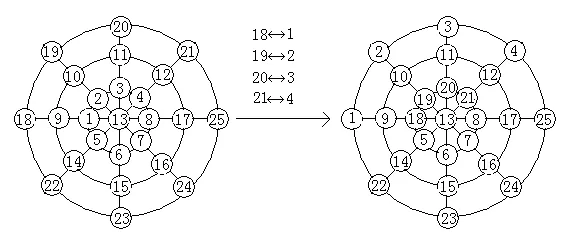
圖10

（作者單位：綏寧縣民族小學）