連續碳纖維增強復合材料汽車頂蓋鋪層優化*

肖志，杜慶勇，莫富灝，韋凱，楊旭靜，邢楊

(湖南大學，汽車車身先進設計制造國家重點實驗室，長沙410082)

連續碳纖維增強復合材料汽車頂蓋鋪層優化*

肖志，杜慶勇，莫富灝，韋凱，楊旭靜，邢楊

(湖南大學，汽車車身先進設計制造國家重點實驗室，長沙410082)

本文中基于抗雪壓性能需求，對連續碳纖維增強復合材料汽車頂蓋結構開展了多層次鋪層優化設計。首先，進行了連續碳纖維增強復合材料力學性能試驗和參數反求，并將分析所得應力應變曲線與試驗結果對比，結果誤差均在允許范圍之內，驗證了所選取的材料本構模型參數的正確性。然后，以頂蓋質量最小化為目標，開展了汽車頂蓋自由尺寸優化、尺寸優化和層組優化，在優化過程中同時兼顧了工藝約束和頂蓋剛度兩個方面的要求。優化后，連續碳纖維增強復合材料汽車頂蓋的質量比原始鋼制件減輕了59.3%，頂蓋在加載過程中未出現明顯的屈曲現象，滿足設計要求。

汽車頂蓋;碳纖維復合材料;鋪層優化;剛度分析

前言

為減少汽車的能源消耗和對環境的污染，輕量化技術得到了廣泛關注。復合材料，尤其是連續碳纖維增強復合材料(carbon fiber reinforced polymer，CFRP)的應用是實現汽車輕量化的重要途徑。CFRP是一種可設計性較強的復合材料，其鋪層方式得到了國內外學者的廣泛研究。

CFRP力學性能表現為各向異性，其力學性能與材料的微觀組分和鋪層方式有密切的關系，因此許多學者在鋪層優化方面做了大量的研究工作。文獻［1］中使用微遺傳算法研究了汽車CFRP下擺臂鋪層順序對其承載能力的影響并獲得最佳鋪層順序。文獻［2］中基于修正PSO算法和Kriging代理模型，對多工況CFRP保險杠開展了相關優化研究。文獻［3］中基于Kriging模型采用遺傳算法對CFRP翼子板的鋪層形式開展了相關研究工作。文獻［4］中使用PSOA算法對復合材料傳動軸進行了鋪層優化設計，并與遺傳算法結果進行了對比，驗證了算法優勢與可行性。文獻［5］中使用優化軟件對CFRP薄壁結構進行了優化研究。近年來針對汽車CFRP構件的優化設計與分析雖已經開展了不少研究，但關于汽車頂蓋的研究仍較少。文獻［6］中針對汽車CFRP頂蓋的生產工藝參數和生產制造過程進行了相關研究。文獻［7］中將CFRP與鋼材相結合并應用到汽車頂蓋制造中，經測試，其材料力學性能優異且在汽車頂蓋抗壓潰工況中取得較好效果。迄今為止，CFRP優化設計研究多是基于矩形板、傳動軸等優化算法的研究，很少有文獻結合工藝可行性開展實際制件的結構設計研究。

本文中基于汽車CFRP頂蓋制造工藝可行性與抗雪壓性能需求，采用自由尺寸優化、尺寸優化和層間組合優化相結合的多層次優化方法對汽車CFRP頂蓋進行了鋪層設計，以兼顧制件工藝要求與性能目標。

1 CFRP力學性能測定

1.1 CFRP樣件制備

在數值分析過程中，材料本構參數的正確獲取與分析結果的準確性有著密切的關系，本文中為獲取材料數值模型本構參數，采用試驗與數值分析相結合的方法，對CFRP開展相關研究。在CFRP板材制備試驗中，碳纖維選用常州市宏發縱橫新材料科技股份有限公司生產的CC-P400－12，樹脂選用惠柏新材料科技(上海)股份有限公司生產的環氧樹脂LTC-6010A/B。在材料制備過程中，依次在真空輔助成型工藝平臺上鋪放下脫模布、碳纖維材料、上脫模布、導流網和真空袋等，當密封性和壓力達到要求的條件時注入樹脂，并在適宜的條件下進行固化處理，從而制備試驗用CFRP板材，如圖1所示。材料制備平臺溫度為35℃，預固化時間為4h，后固化溫度為80℃，后固化時間為4h。

1.2 力學性能試驗與參數反求

在制備試樣板材基礎上，為正確獲取CFRP數值模型本構參數，開展了材料單向拉伸試驗和三點彎曲力學性能試驗，并根據試驗結果反求材料本構參數，從而保證數值分析模型參數的準確性。CFRP單向拉伸試驗和三點彎曲試驗分別在微機控制電子萬能試驗機CMT5105和CMT4304上進行。其中，單向拉伸試驗參照標準GB/T 3354—1999［8］進行，拉伸速率為2mm/min，環境溫度為23℃，樣件選用標距(測量長度)為50mm、厚度為1.96mm的8層CFRP試樣。三點彎曲試驗參照標準GB/T 1449—2005［9］進行，加載速率為2mm/min，環境溫度為23℃，樣件選用跨距為26mm、厚度為2.01mm的8層CFRP試樣，試驗結果如圖2所示。

圖1CFRP板材制備及其試樣

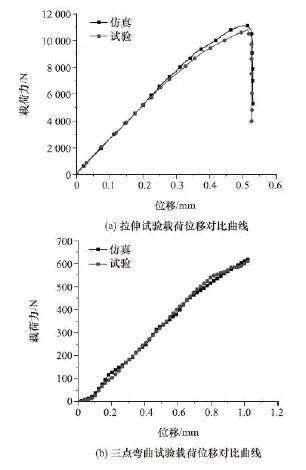
圖2 材料力學性能試驗與分析對比曲線

由于材料試驗只能獲得試件的宏觀應力應變曲線等數據，而無法獲得試件全場的應力應變分布和損傷演化的具體過程。本文中基于有限單元法建立了CFRP力學性能數值分析模型，在力學性能試驗基礎上通過材料數值模擬反求材料本構參數，其流程如圖3所示。

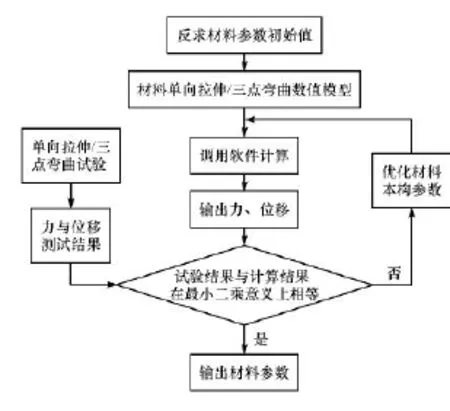
圖3 材料參數反求流程圖

在CFRP數值分析過程中，通過定義殼單元沿厚度方向的積分點數量來定義復合材料鋪層數量，一個積分點代表一個復合材料鋪層，每個積分點處的材料坐標系旋轉角度代表單層碳纖維的鋪層方向角［10］。CFRP失效模擬方式為Chang-Chang失效準則［11－12］，該準則包含了4種失效準則，即纖維拉伸破壞、纖維壓縮破壞、基體開裂和基體擠壓［13－14］，該失效準則的具體表達式如下。

對于纖維拉伸模式σ11＞0，則E1=E2=E12=μ12= μ21=0且判斷

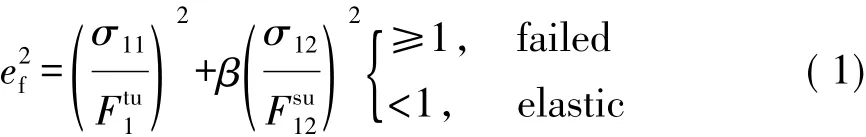
對于纖維壓縮模式σ11≤0，則E1=μ12=μ21=0且判斷

對于基體拉伸模式σ22＞0，則E2=μ21=G12=0且判斷

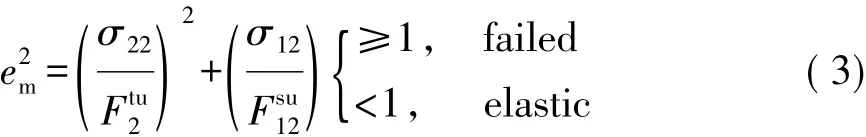
對于基體壓縮模式σ22≤0，則E2=μ21=μ12=G12=0且判斷

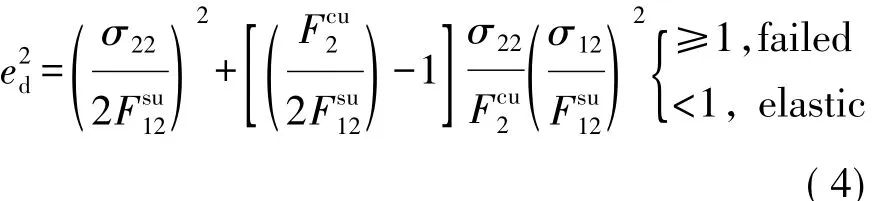
式中:E1，E2，E12分別為縱向彈性模量、橫向彈性模量、面內剪切模量;β為剪切應力比例系數，可人為地定義在纖維拉伸模式下剪切所占的權重，當β=1時，計算失效準則相當于Hashin失效準則，當β=0時，式(1)將等效為最大應力準則，通常情況下，β無法通過試驗來獲取，需要經過試錯法進行標定;μ12，μ21分別為主泊松比及次泊松比;Ftu1，Ftu2，Fcu1，Fcu2，Fsu12分別為縱向拉伸強度、橫向拉伸強度、縱向壓縮強度、橫向壓縮強度、面內剪切強度;σ11，σ22和σ12分別為材料在軸向方向、橫向方向和面內方向承受的應力;ef，ec，em，ed分別為各模式下判斷失效與否的參數。采用LS-DYNA軟件對CFRP力學性能進行數值分析，并經試驗驗證，材料力學性能試驗與數值模擬如圖4所示，反求所得材料力學性能參數如表1所示。通過力學性能試驗與數值分析曲線(如圖2所示)對比可以看出，CFRP在準靜態拉伸斷裂前，應力應變曲線趨近于線性變化，材料表現為線彈性性質，無明顯的屈服特征。同時，由準靜態單向拉伸應力應變曲線可以明顯看出CFRP斷裂失效表現為明顯的脆性斷裂特征。

圖4 材料力學性能試驗與仿真分析

表1 CFRP力學性能參數

2 CFRP汽車頂蓋數值模型

采用ABAQUS軟件對汽車頂蓋進行雪壓分析時，取車身上半部作為研究對象，網格基本尺寸為5mm×5mm，四邊形單元和三角形單元類型分別為S4R和S3，CFRP制件與鋼制件之間采用膠粘模擬，膠粘單元類型選為COH3D8，對車身側圍截斷位置約束X，Y，Z 3個方向的平動，評判頂蓋在重力載荷、1.28kPa的雪壓工況及卸掉雪壓載荷3種工況條件下CFRP汽車頂蓋是否會發生屈曲現象，雪壓分析有限元模型如圖5所示。加載過程中，根據汽車頂蓋在室外積雪過程的實際情況，將一個復雜的非線性動載問題簡化為分布均勻加載的靜態剛強度試驗問題。同時，將乘用車頂蓋積雪這一隨機過程量化，通過分析加載前后頂蓋位移變化來評判頂蓋在積雪過程中是否出現永久變形和屈曲現象，以此來評判優化結果的可行性。數值分析采用隱式靜態幾何非線性算法，考慮了幾何非線性、邊界條件非線性和卸載后的殘余變形，對CFRP汽車頂蓋進行雪壓屈曲分析，了解CFRP汽車頂蓋的承載與變形能力，判斷是否滿足汽車頂蓋剛度要求。

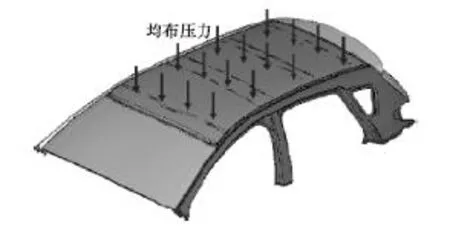
圖5 汽車頂蓋雪壓分析數值模型

3 CFRP汽車頂蓋鋪層優化設計

3.1 初始模型雪壓分析

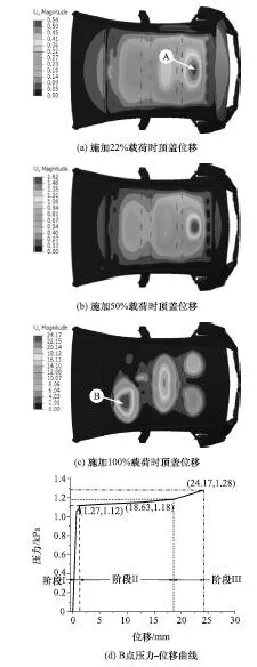
圖64 層CFRP汽車頂蓋雪壓變形過程

考慮到CFRP性能和汽車頂蓋輕量化要求，在初步設計階段采用4層CC-P400－12作為環氧樹脂LTC-6010A/B的增強材料，厚度約為1.0mm，并通過數值分析來校核頂蓋剛度是否滿足相關要求，模擬積雪壓力時頂蓋位移變化簡圖和最大變形位置的壓力-位移曲線，如圖6所示，其中，數值模型在施加壓力時載荷采取線性增加方式。由圖6(a)～圖6 (c)位移變化云圖可知，4層CFRP汽車頂蓋位移隨著壓力的增加而增大，且初始最大變形位置發生在CFRP汽車頂蓋后橫梁與后支撐梁之間的A點;隨后載荷繼續增加，最大變形位置由A點轉移到B點。由圖6(d)可見，在4層CFRP汽車頂蓋受壓初始階段(階段Ⅰ)具有較好的抗變形能力;當壓力達到1.12kPa時(階段Ⅱ)，4層CFRP汽車頂蓋位移由1.27mm激增至18.63mm，這表明4層CFRP汽車頂蓋出現幾何軟化響應，發生屈曲現象［15］;而后當壓力達到1.18kPa后(階段Ⅲ)，4層CFRP汽車頂蓋剛度繼續增加，最大變形達到24.17mm。由于4層CFRP汽車頂蓋在受壓過程中出現屈曲現象，故無法滿足雪壓剛度要求。

3.2 CFRP汽車頂蓋鋪層優化設計

由4層CFRP汽車頂蓋剛度計算結果可知，在

頂蓋受載過程中該鋪層方案無法滿足相應的雪壓分析要求，故在同時考慮制造工藝約束和頂蓋雪壓分析要求的條件下對CFRP汽車頂蓋進行鋪層優化設計。在優化設計過程中采用自由尺寸優化，尺寸優化和復合材料層組優化3種優化方法，優化流程如圖7所示。

3.2.1 自由尺寸優化

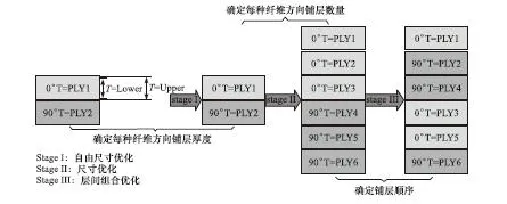
圖7 鋪層優化設計流程

在初始設計過程中，汽車CFRP頂蓋剛度能較好地滿足剛度要求，通過自由尺寸優化來獲取每種鋪層角度的最佳鋪層厚度。在自由尺寸優化過程中為復合材料建立與鋪層角度相對應的幾個超級層，該階段每一鋪層角度所在超級層厚度可連續變化。優化時，對各纖維鋪層角度的鋪層厚度進行優化，優化約束為汽車CFRP頂蓋任意節點位移，優化目標為汽車CFRP頂蓋質量最小，優化數學表達式如下所示:

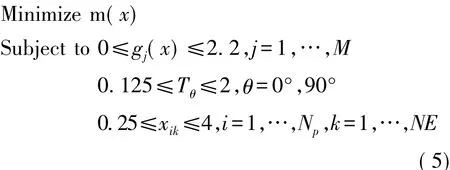
式中:m(x)為頂蓋質量;gj(x)為第j個約束響應;M為總的約束數量;Tθ為對應鋪層角度的鋪層厚度; xik為第i個超級層中第k個單元的厚度;NE為單元數量;Np為超級層數量。

為使結構能較好地滿足裝配工藝和制造工藝要求，在優化設計過程中取制件總體厚度為制造約束目標:

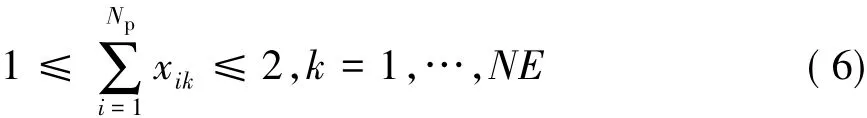
從而使得優化結果更好地滿足實際要求。

3.2.2 尺寸優化

通過自由尺寸優化，能較好地確定每種鋪層角度所需的鋪層厚度，但由于層合板在制備過程中有一定的厚度要求，且鋪層數量對制件的力學性能均有較大影響，所以研究中通過尺寸優化設計將制件單層厚度與設計變量之間的關系進行耦合分析，以獲得每種鋪層角度在給定鋪層厚度條件下的最佳鋪層數量。尺寸優化數學模型除采用與自由尺寸優化相同的模型外，還需建立多個設計變量之間的關系［16］。尺寸優化設計過程中，一個設計變量與其他設計變量間的關系可表示為

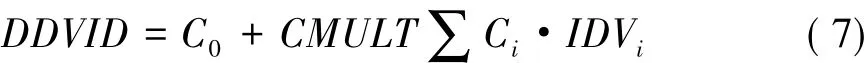
式中:DDVID為該階段最終的優化設計變量;C0為一常量;IDVi為獨立變量標識;Ci為IDVi的系數; CMULT為常量系數。

因此鋪層厚度設計變量之間的關系可表示為

式中:T為總的鋪層厚度變量;取C0=0;CMULT=1; Ci=1。

在該優化過程中，同時兼顧了工藝制造過程中單層結構的制件厚度，在本次優化設計過程中設置每一鋪層角度單層結構的厚度是相等的，即取t= 0.25mm［2］，在前期優化所得單種角度厚度基礎上計算制件總的鋪層層數:

式中:Ni為每種鋪層角度對應的鋪層層數;Ti為每個角度對應的總的鋪層厚度。

在該優化設計過程中，對每一纖維鋪層角度的厚度變量都進行了計算，并最終確定了每一纖維鋪層角度所需的最佳鋪層層數和CFRP汽車頂蓋所需設計的總的厚度尺寸。

3.2.3 層組優化

CFRP的力學性能與纖維角度的排列順序有著緊密的關系，在層組優化階段，實際的目的是為了獲得結構的最大剛度系數矩陣，從而使結構的剛度達到最大。在CFRP制備過程中，鋪層結構設計應避免固化過程中由于彎曲、拉伸和扭轉等耦合效應引起的翹曲變形和樹脂裂紋，為此在鋪層設計過程中應避免使用同一方向的鋪層組，如果使用，應不多于4層［17］。在層組優化設計階段考慮了該制造工藝約束，因此本文中選取同一鋪層角度連續鋪層數量最多為兩層，以使頂蓋制造能較好地滿足制造工藝要求。

經自由尺寸優化、尺寸優化和層組優化后得到CFRP頂蓋鋪層數量為6層，鋪層順序為［0/90/90/ 0/0/90］，單層厚度為0.25mm，如圖8所示，其中11 101～11 103及12 101～12 103分別代表各鋪層組編號。

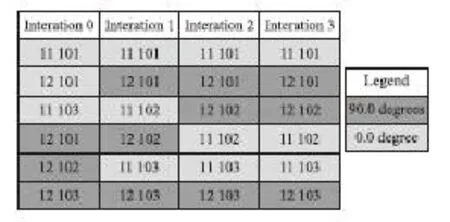
圖8CFRP頂蓋鋪層順序優化結果

3.3 優化結果與分析

經自由尺寸優化、尺寸優化和層組優化之后，對CFRP汽車頂蓋再次進行雪壓分析，分析結果表明，6層CFRP汽車頂蓋在進行數值分析的過程中，頂蓋最大變形量為1.922mm，與鋼制頂蓋分析結果0.769mm對比可見，雖然變形量大于鋼制頂蓋變形量，但變形依然處于彈性范圍之內，未出現明顯的屈曲現象，且在整個分析過程中，6層CFRP頂蓋的位移變化趨勢比4層CFRP頂蓋穩定，因此判斷6層 CFRP頂蓋未出現明顯的屈曲現象，剛度能滿足要求，最終頂蓋位移云圖和頂蓋壓力-位移變化曲線如圖9和圖10所示。

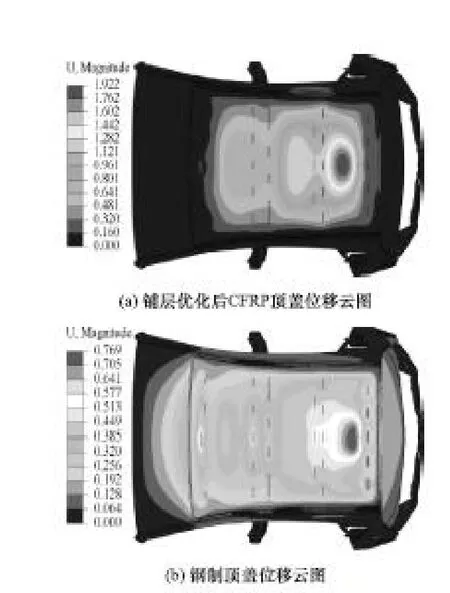
圖9 頂蓋分析位移云圖

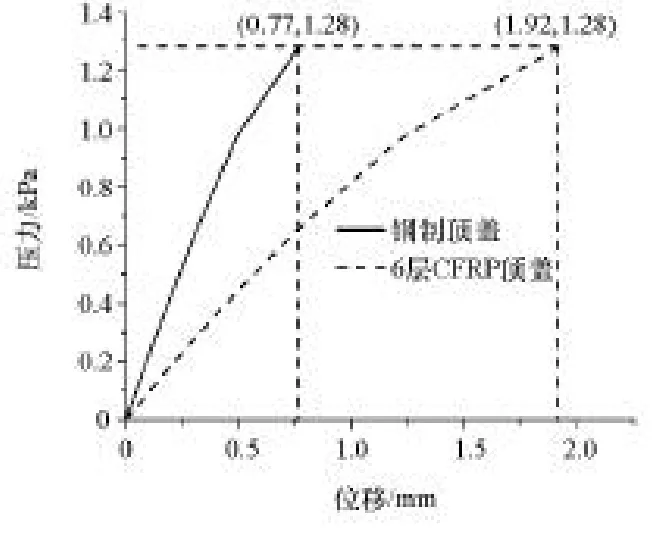
圖10CFRP頂蓋和鋼制頂蓋壓力位移曲線

通過優化使CFRP頂蓋在滿足剛度及工藝制造等因素的條件下質量有了較大幅度的減小，結果如表2所示。鋼制頂蓋初始質量為10.944kg，汽車CFRP頂蓋優化設計前的設計標準質量為8.906kg，優化后頂蓋質量降低至4.453kg，較設計標準質量減輕了50%，與鋼制件相比減輕了59.3%，如圖11所示。

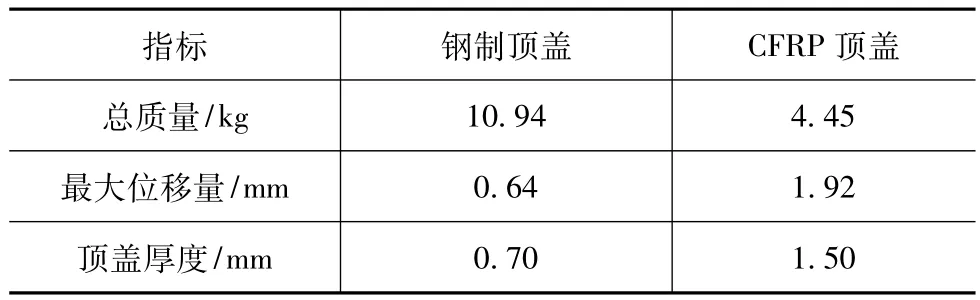
表2 頂蓋優化設計分析結果

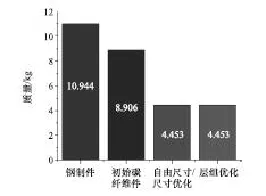
圖11 頂蓋優化前后質量對比

4 結論

本文中圍繞汽車CFRP頂蓋鋪層優化設計開展了材料制備、材料力學性能測定和數值模擬分析，并最終通過自由尺寸優化、尺寸優化和層組優化，完成了汽車CFRP頂蓋鋪層優化設計，得出以下結論。

(1)CFRP數值模擬曲線與力學性能試驗曲線對比結果，誤差在5%以內，驗證了CFRP建模的有效性、選用材料本構模型參數和失效準則可用于后續的數值模擬。

(2)在優化過程中同時兼顧了制造工藝約束和制件剛度兩方面的要求，較好地克服了僅使用理論算法控制制件剛度的局限性，使制件在滿足剛度要求的同時，成型工藝可行性更好。

(3)將CFRP與傳統的鋼材對比發現，CFRP剛度和強度都較金屬材料有較大的提升，尤其是在汽車結構輕量化方面的效果顯著，通過優化，汽車CFRP頂蓋質量比鋼制頂蓋減輕了59.3%。

［1］KIM D H，CHOI D H，KIM H S．Design optimization of a carbon fiber reinforced composite automotive lower arm［J］．Composites Part B:Engineering，2014，58:400－407．

［2］LIU Z，LU J，ZHU P．Lightweight design of automotive composite bumper system using modified particle swarm optimizer［J］．Composite Structures，2016，140:630－643．

［3］程章，朱平，馮奇，等．碳纖維復合材料汽車翼子板優化設計研究［J］．汽車工程學報，2015，5(5):367－374．

［4］MANJUNATH K，RANGASWAMY T．Ply stacking sequence optimization of composite driveshaft using particle swarm optimization algorithm［J］．International Journal for Simulation and Multidisciplinary Design Optimization，2014，5:A16．

［5］嚴君．基于OptiStruct碳纖維復合材料薄壁結構優化設計研究［D］．太原:中北大學，2012．

［6］REICHWEIN H G，LANGEMEIER P，HASSON T，et al．Light，strong and economical epoxy fiber reinforced structures for automotive mass production［C］．Detroit，2010:1－20．

［7］BAMBACH M．Fibre composite strengthening of thin steel passenger vehicle roof structures［J］．Thin-Walled Structures，2014，74:1－11．

［8］GB/T 3354—1999定向纖維增強塑料拉伸性能試驗方法［S］．1999．

［9］GB/T 1449—2005．纖維增強塑料彎曲性能試驗方法［S］．2005．

［10］楊旭靜，張振明，鄭娟，等．復合材料前防撞梁變截面多工況多目標優化設計［J］．汽車工程，2015，37(10):1130－1137．

［11］Livemore Software Technology Corporation．LS-DNA keyword user's manual［G］．California:Livemore Software Technology Corporation，2001．

［12］張振明．變厚度復合材料汽車防撞梁優化設計研究［D］．長沙:湖南大學，2014．

［13］FERABOLI P，WADE B，DELEO F，et al．LS-DYNA MAT54 modeling of the axial crushing of a composite tape sinusoidal specimen［J］．Composites Part A:Applied Science and Manufacturing，2011，42(11):1809－1825．

［14］DUAN S，TAO Y，HAN X，et al．Investigation on structure optimization of crashworthiness of fiber reinforced polymers materials［J］．Composites Part B:Engineering，2014，60:471－478．

［15］Van Veldhuizen B，Kranendonk W，Ruifrok R．The relation between the curvature of horizontal automotive panels，the panel stiffness and the static dent resistance［J］．Materials and Body Testing IBEC，1995，95:62－70．

［16］李楚琳，張勝蘭，馮櫻，等．HyperWorks分析應用實例［M］．北京:機械工業出版社，2008．

［17］沈真，章怡寧．復合材料結構設計手冊［M］．北京:航空工業出版社，2001．

Ply Optimization on Vehicle Roof of Continuous Carbon Fiber Reinforced Polymer

Xiao Zhi，Du Qingyong，Mo Fuhao，Wei Kai，Yang Xujing＆Xing Yang
Hunan University，State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body，Changsha410082

In this paper，multi-layer ply optimization for the vehicle roof of continuous carbon fiber reinforced polymer(CFRP)is conducted based on the requirements of anti-snow performance．Firstly，material mechanical properties test for CFRP and inverse identification of material parameters are performed，and the stressstrain curves obtained by numerical simulation are compared with test results with errors within allowed range，verifying the rightness of material constitutive model parameters defined．Then，with minimizing roof mass as objective，free-size optimization，size optimization and ply stacking optimization on CFRP vehicle roof are carried out with both process constraints and stiffness requirements concurrently considered．After optimization the mass of CFRP roof is 59.3%lighter than that of original steel one，and no obvious bucking occurs during roof loading，meeting design requirements．

vehicle roof;CFRP;ply optimization;stiffness analysis

10．19562/j．chinasae．qcgc．2017．06．018

*國家自然科學基金(51475154，51405150)和湖南大學汽車車身先進設計制造國家重點實驗開放基金(31475006)資助。

原稿收到日期為2016年5月4日，修改稿收到日期為2016年8月13日。

莫富灝，助理教授，E-mail:fuhaomo@hnu．edu．cn。