基于工藝特征約束的改進遺傳算法①

張 節, 沈建新, 田 威

(南京航空航天大學 機電學院, 南京 210016)

基于工藝特征約束的改進遺傳算法①

張 節, 沈建新, 田 威

(南京航空航天大學 機電學院, 南京 210016)

為提高飛機裝配的精度, 減小定位的誤差, 優化具有復雜工藝特征的機身框件的支撐序列. 針對優化中工藝特征約束處理問題, 建立了工藝特征約束的廣義數學模型, 從理論角度提出了一種針對此類約束的不可行解修補算法, 并基于此算法設計一種改進的遺傳算法. 使用改進的遺傳算法優化某型飛機機身框在可重構柔性工裝上的支撐序列, 優化過程穩定, 最優序列下框的柔性定位誤差減小93.08%, 保證了飛機裝配的精度. 理論基礎分析和仿真結果分析表明, 改進的遺傳算法通用性強, 適用于各種約束優化問題; 收斂速度快且穩定, 具備可行性.

裝配精度; 遺傳算法; 約束優化; 修補算法; 工藝約束; 飛機裝配

隨著現代飛機制造技術的發展, 飛機產品的快速更新換代, 飛機裝配已逐漸向自動化、數字化發展, 可重構柔性裝配工裝以其可變性與通用性的特點廣泛應用于國外數字化裝配領域, 國內也開始重點發展這一項智能裝備技術. 裝配過程伴隨著誤差的產生, 如果誤差累積過大, 會導致飛機的關鍵裝配特性超出其目標值, 對裝配質量和周期造成嚴重的影響[1]. 因此, 對裝配件的定位誤差控制已成為急需解決的問題. 定位誤差的來源分為剛性和柔性兩部分[2]. 其中剛性部分主要來源于工裝的制造和安裝, 郭飛燕等[3]建立了誤差模型,并用補償法抑制了該種誤差; 柔性部分主要來源于裝配件的形變, 這也是本文研究的目的, 即通過優化定位/支撐的點陣布局來抑制柔性定位誤差.

考慮到飛機框件的復雜工藝特征, 框件在可重構柔性工裝上的支撐序列優化可以作為一種具有工藝特征約束的約束優化問題來處理. 其中, 工藝特征約束是約束條件在實際中的體現, 從狹義角度, 以機身框件為例, 主要包括交錯布置的加強筋和不規則的邊緣形狀等工藝特征; 從廣義角度, 主要包括等式、不等式約束和設計變量定義區間約束(如設計變量定義區間不連續且設計域離散). 求解約束優化問題的算法包括確定性算法和智能型算法[4]. 確定性算法(如投影梯度法、牛頓法、拉格朗日法等)要求目標函數在定義域內連續可微, 因此具有離散設計域約束優化問題無法解決.而智能優化算法在設計相對應的約束處理技術后, 均可用于求解約束優化問題. 鑒于智能優化算法是一類基于無約束的優化搜索技術, 在工程中使用智能算法處理約束優化問題時, 需要設計一種相對應的約束處理技術[5]. 約束處理技術作為當今研究熱點, 常見的包括懲罰函數法、轉化法、解碼法等[6]. 懲罰函數法是最常用的方法, 通過在適應值函數上加懲罰項, 從而將約束問題變為無約束問題. BARBOSA等[7]提出一種基于違反約束程度的自適應懲罰函數法處理約束優化問題;與其相似的還有HO PY[8]和DEB K[9], DEB K將自適應策略用于增廣拉格朗日乘子法, 提出改進的約束優化遺傳算法, 試驗證明該法具有高效性和精確性; 此外,還有MONTEMURRO[10]提出的自動動態懲罰函數法.轉化法是另一熱門技術, 該法直接將違反約束條件程度轉化為優化目標, 從而將約束優化轉化為無約束多目標優化問題, 如王俊年等[11]從多目標優化方法的角度出發, 將約束違背程度作為新的優化目標完成約束優化; TAKAHAMA T和SAKAI S[12]提出α約束法, 該法采用約束滿足水平表示個體滿足約束條件的程度. 轉化法或將個體區分為可行解和不可行解分別處理, 如林丹[13]提出調整違反約束條件程度閾值的方式, 自適應確定不可行解比例. 其它約束處理技術也是當今研究熱點, 如王曉圓等[14]針對遺傳算法中染色體, 提出染色體的約束檢查和調整技術, 解決了復雜約束問題; 甘敏[15]等將多目標優化法和自適應懲罰函數法結合, 提出穩健的新方法; Zhang C等[16]改進元啟發式算法, 提高其搜索性能的同時引入可行性與支配性規則, 并驗證了算法在處理約束優化問題時的精度和效率.

然而, 這些已有處理技術對不可行解通常采用“保留并改善”的對策, 依靠優化操作過程本身來處理. 在框件支撐序列優化中工藝特征約束下, 算法隨機性將在運行過程中產生大量不可行解, 從而影響找到可行解的概率; 且由于需要將優化程序與ANSYS等其他大型軟件聯合使用, 這些已有技術產生的不可行解常造成算法效率低、穩定性差甚至不可行等問題. 因此, 設計一個計算復雜度低、能處理工藝特征約束條件的約束處理算法, 具有一定的工程意義. 考慮到相比于其它算法, 遺傳算法不涉及搜索的方向、步長等參數, 且不失一般性, 本文面向交點孔定位的框件, 優化其支撐序列來減小裝配中的定位誤差. 針對支撐序列優化中的工藝特征約束, 提出一種不可行解修補算法, 并依此改進遺傳算法, 完成優化, 最后驗證該算法的可行性.

1 修補算法的原理

1.1 工藝特征約束的廣義數學模型和分析

不失一般性, 設優化問題有n個獨立的設計變量xi(i=1, 2,…, n), 則工藝特征約束(如圖1)的廣義數學模型如式(1)所示. 即變量在上下界中有m個不連續的定義區間; 有k個獨立變量滿足等式約束, l個獨立變量滿足不等式約束.

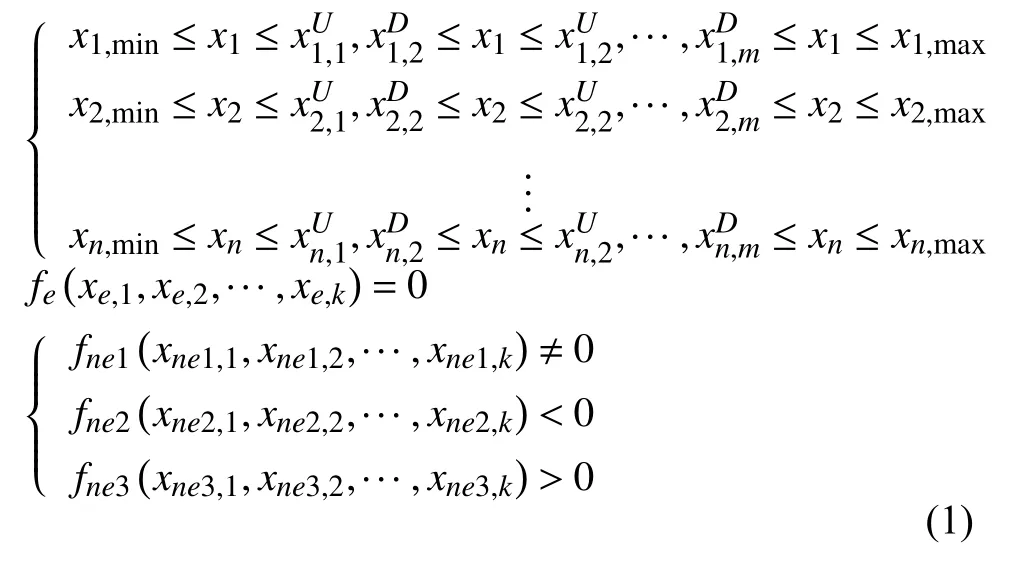
其中xn,min、xn,max為設計變量極值,為區間邊界.

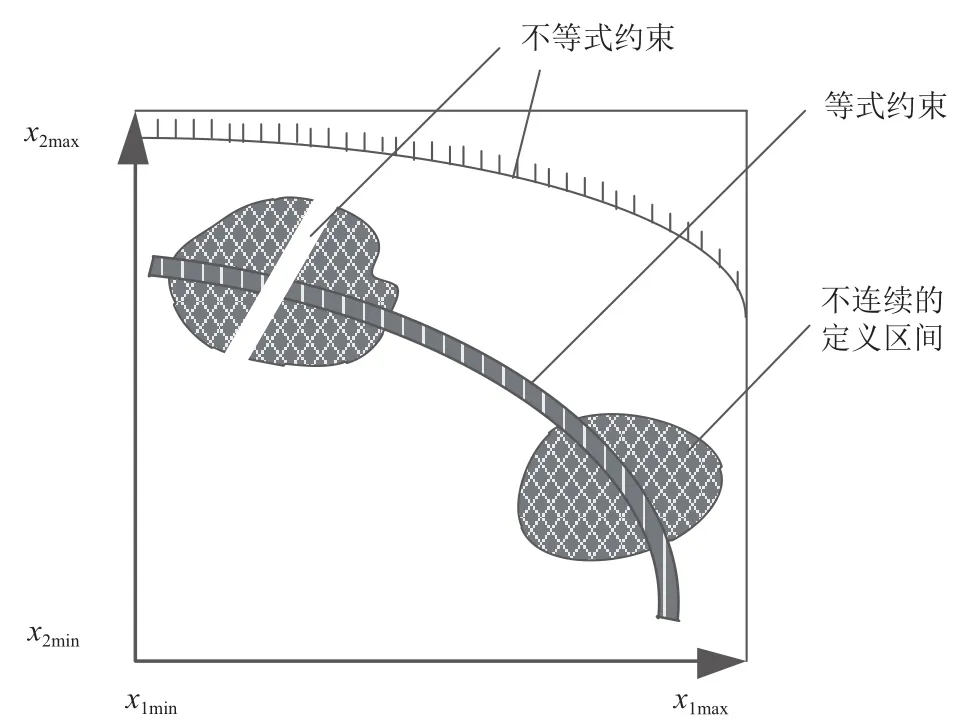
圖1 2個設計變量時的2維離散設計域

因此, 約束優化迭代過程中, 設計變量的解將產生以下四種問題:

(1) 設計變量不滿足定義區間約束;

(2) 設計變量不滿足等式約束;

(3) 設計變量不滿足不等式約束;

(4) 設計變量無解(沒有滿足約束的解).

對于第四種問題, 其產生的原因在于約束過多, 解決方法為重新建立優化數學模型, 本文不再贅述. 對于前三種問題, 本文提出一種有效的修補算法思路: 先處理違反等式約束的問題, 再處理違反不等式約束的問題, 最后處理定義區間約束的問題.

1.2 算法流程

針對任一設計變量xi進行討論, 設其在上下界區間內具有不連續的定義區間(如圖2).

圖2 設計變量不連續定義區間

Step1. 檢查xi是否處于中. 若否, 則在內隨機生成新值(如圖3(a));

Step2. 檢查xi是否滿足等式約束. 若否, 根據等式

fe=0獲取xi與其他設計變量的關系, 在內調整xi, 并相應調整其他設計變量, 使等式約束條件成立(如圖3(b));

Step3. 檢查xi是否滿足不等式約束. 若否, 根據不等式獲取xi與其他設計變量的關系, 在中滿足等式約束的區間內調整xi, 并相應調整其他設計變量, 使等式約束條件成立的同時不等式約束條件也成立(如圖3(c));

Step4. 檢查xi是否落入不連續的定義區間. 若否,則在滿足等式與不等式約束的區間內調整xi至定義區間,同時根據上述變量關系相應調整其它未落入區間的設計變量, 直至所有設計變量落入定義區間(如圖3(d)).

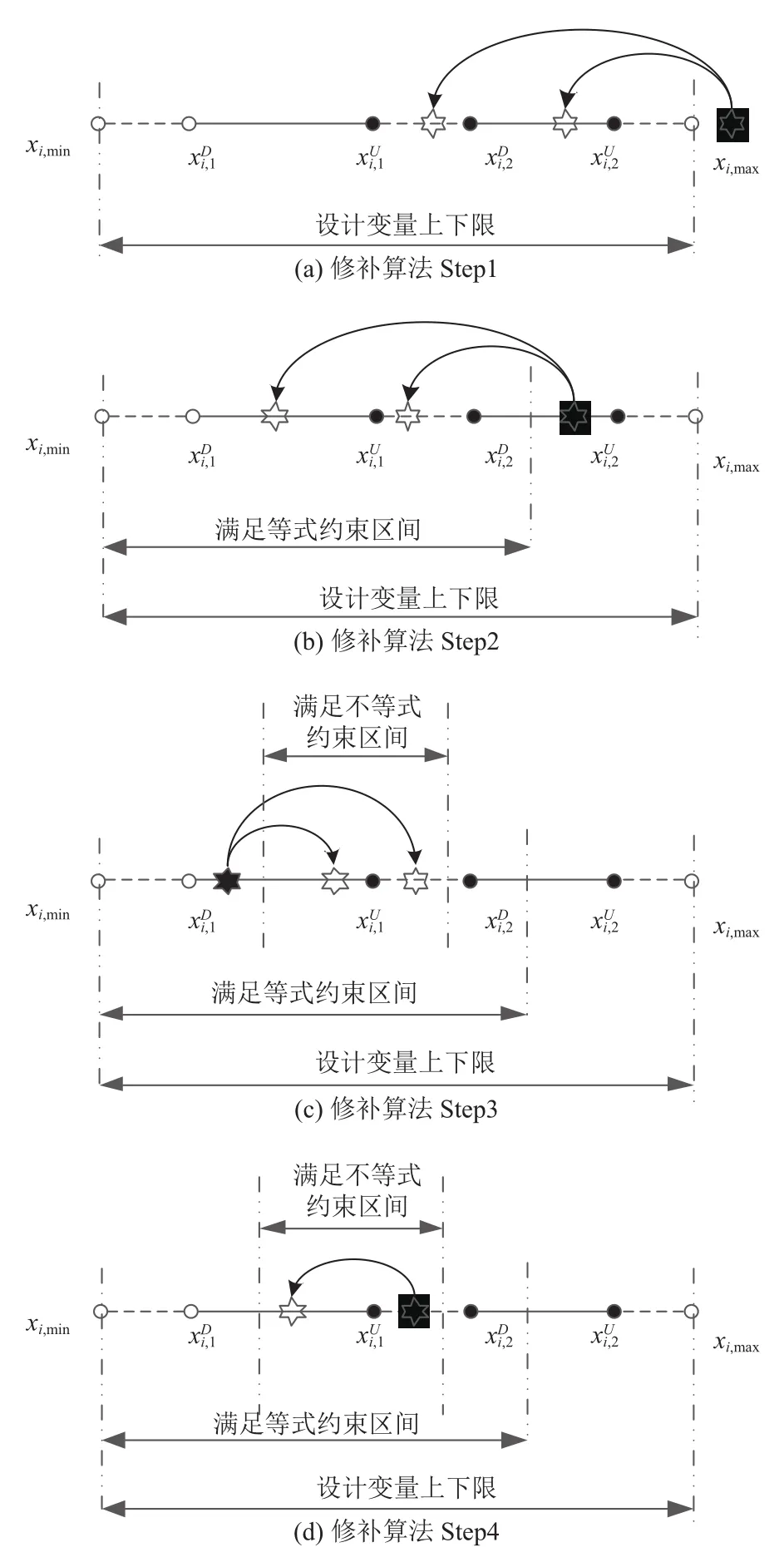
圖3 修補算法圖解

1.3 算法復雜度分析

由上述流程可得, 算法偽代碼如下:

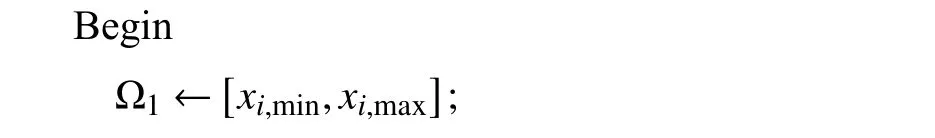
不失一般性, 假設設計變量的個數為n, 且所有設計變量均在變量上下界之外, 則該算法的復雜度如式(2):

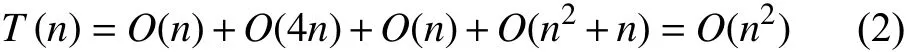
由復雜度可知, 該算法計算復雜度低, 且設計變量越少越簡單. 因此, 進行基于該算法的優化之前, 可以使用靈敏度分析簡化設計參數, 以增大優化效率.

2 改進遺傳算法及工程應用

2.1 背景介紹

飛機裝配是指將大量的飛機零件、標準件等按設計要求和技術條件在工藝裝備上進行結構鉚接、系統安裝等全過程[17]. 為保證飛機裝配的精度, 需要采用大量的裝配工裝[18]. 可重構柔性工裝作為裝配工裝的前沿產品, 實現數字量在飛機制造過程中的全流通, 其關鍵技術的突破將為相關行業的發展帶來巨大的機遇[19].可重構柔性工裝關鍵技術中, 裝配件支撐/定位方案的設計與優化成為解決定位誤差的方法之一, 同時也是近幾年的研究熱門. 張洪雙等[20]設計了一種三坐標數控定位器, 并使用遺傳算法優化了定位器的布局和最優行程; 金棟平等[21]針對機翼后緣的柔性支撐結構, 完成了其布局優化設計; 蓋玉春等[22]對飛機調姿工裝的支撐位置進行了優化; XIONG L等[23]和LU C等[24]分析了“N-2-1”定位原則, 并使用遺傳算法優化了薄壁件的支撐序列, 以減小加工過程中的形變定位誤差.

本文筆者所在課題組針對某型飛機機身的立式裝配設計了一種可重構柔性工裝. 基于框件的交點孔定位方式, 該工裝由4根筒狀定位器進行“銷-孔”定位與支撐. 由于框件在裝配中因柔性形變而引起定位誤差, 考慮到裝配精度要求(0.05 mm)的要求, 定位器的布置序列需要優化.

2.2 優化數學模型

采用遺傳算法對框的支撐序列進行優化, 將4根支撐件中心的極坐標作為設計變量, 中心點坐標處于可行域內(如圖4)作為約束條件, 框的最大形變定位誤差作為目標函數, 其數學模型如式(3):

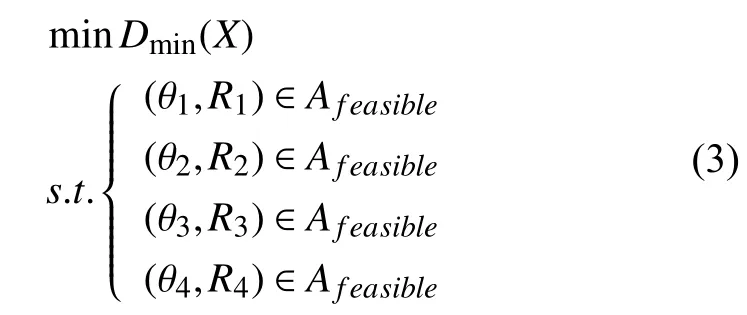
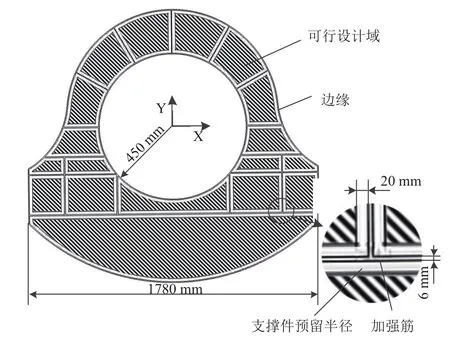
圖4 支撐中心點在工藝特征約束下的可行設計域

2.3 面向飛機裝配的工藝特征約束分析

在該框件的支撐序列優化中, 工藝特征約束在廣義上涉及不連續的定義區間和不等式約束. 例如, 當θ=1.5π時, 其約束類型在極坐標下如圖5所示.

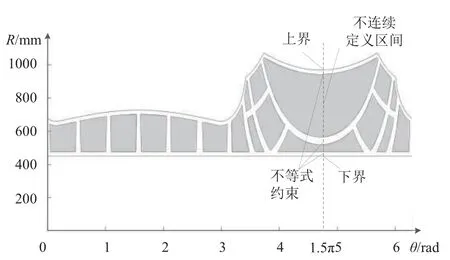
圖5 某型飛機機身框的工藝特征約束

其不連續定義區間的約束在狹義層面上體現于加強筋和邊緣的約束. 為了孔的位置不在加強筋上, 且定位器與加強筋不發生干涉, 需要使支撐件與加強筋和邊緣保持一定距離. 同時, 加強筋布置的復雜性和邊緣曲線的不規則性, 導致設計域被分隔為很多不規則的塊, 即離散的設計域.

其不等式約束在狹義層面上體現于極坐標下兩個坐標參數之間的關系. 因為框的邊緣為不規則的曲線,極坐標下框上各點的半徑與角度成函數關系, 因此合理的半徑應該處于各角度對應的最大值與最小值之間.

2.4 改進的遺傳算法

考慮到框件中工藝特征約束, 需要對優化算法進行約束處理. 然而常規的懲罰函數法等處理技術在該類工程問題中復雜、低效、穩定性差, 且優化過程中不可行解無法在導入ANSYS等有限元軟件后完成仿真分析, 嚴重制約優化的可行性. 因此, 基于上述修補算法改進遺傳算法.

改進后的遺傳算法流程如下:

Step1. 設定參數, 生成滿足工藝約束條件的初始種群, 種群中個體為所有支撐點的坐標信息;

Step2. 使用ANSYS軟件進行有限元仿真分析, 計算所有個體對應的工件最大形變量;

Step3. 進入遺傳操作循環;

Step4. 適應度值計算, 選出種群中的精英解;

Step5. 對種群執行選擇操作;

Step6. 對種群執行交叉操作;

Step7. 對種群執行變異操作;

Step8. 使用修補算法修正種群;

Step9. 使用ANSYS軟件仿真分析新種群個體對應的工件最大形變量, 使用精英解淘汰并替換產生形變量較大的個體, 得到新一代種群;

Step10. 判斷是否達到停止標準, 即判斷是否達到最大迭代次數, 或工件上最大形變量小于形變許用值且穩定于該最優值. 若已到, 則輸出最優解, 程序停止.若未到, 則轉到Step3.

該改進的遺傳算法流程圖如圖6所示.

3 優化結果及討論

(1) 通過運行改進的遺傳算法, 迭代得到用于支撐/定位用的交點孔的最佳序列, 即框的最佳支撐序列如圖7所示. 圖中各交點孔的位置在框內且保證了定位器不與框產生干涉. 框件在最佳支撐序列下最大誤差為0.02091 mm, 滿足裝配要求(0.05 mm), 且相比于原始設計方案(0.3022 mm)減小93.08%. 綜上可以看出該改進的算法具有可行、有效性.

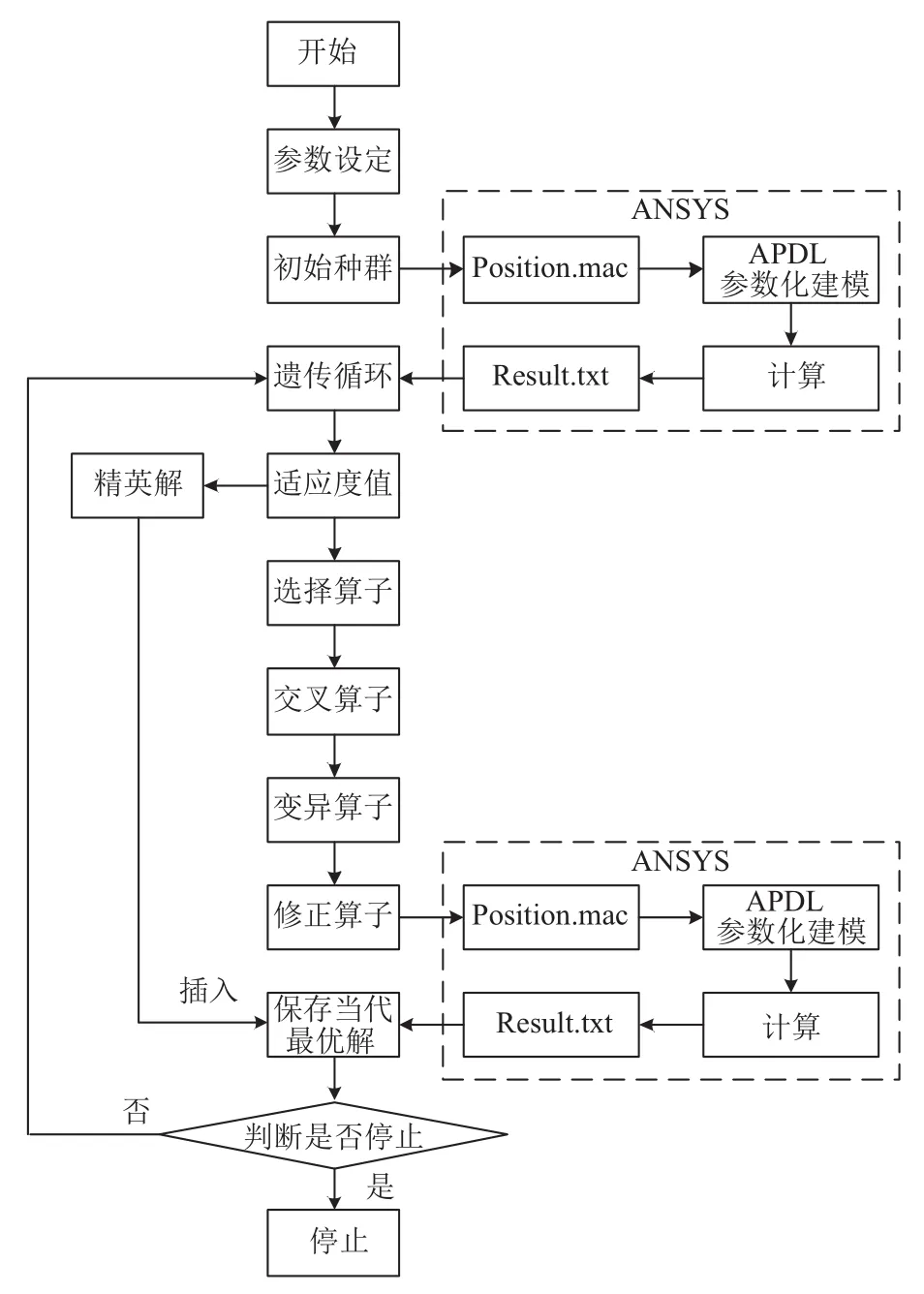
圖6 改進的遺傳算法流程圖

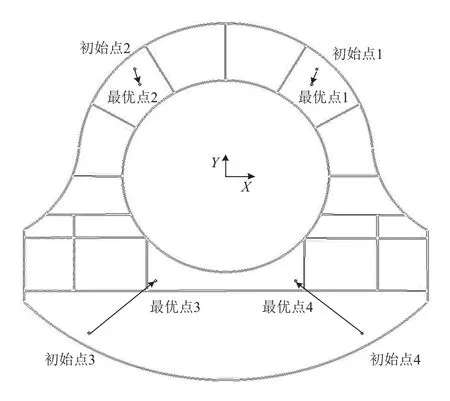
圖7 最優的支撐序列

(2) 選擇種群分別為40、60、80、100進行試驗,優化過程迭代圖如圖8所示. 由此可見, 該算法收斂速度快, 平均在25代左右收斂, 具有較好的優化效率. 優化運行過程中, 外部調用的有限元軟件未出現因不可行解而計算失敗的問題. 相比靜態、動態懲罰函數法,各方法在初代種群完成第一代遺傳操作后可行解的平均個數(50次獨立仿真)如圖9所示. 由此可得, 該算法具有較好的穩定性.

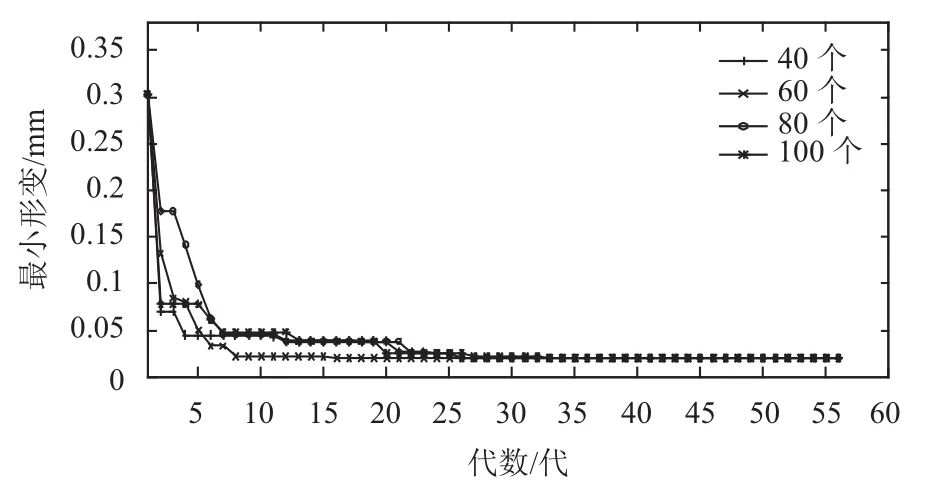
圖8 優化算法曲線圖

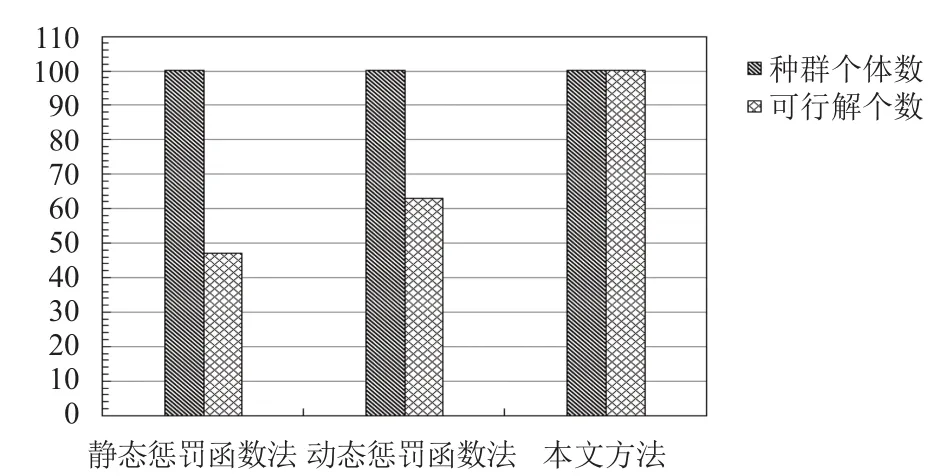
圖9 不同算法可行解個數對比

(3) 對比優化前后框件的形變云圖(如圖10)可知,優化算法將支撐點靠近加強筋布置密集的部位, 使框內產生較大形變的部位轉移到了加強筋布置密集的地方, 這樣能夠使加強筋承擔更多的載荷, 在保證整體最大形變量顯著減小的同時, 減小裝配過程中需要鉚接的部位(即邊緣部位)的形變誤差, 從而保證鉚接的精度.

(4) 本文針對工藝特征約束在狹義層面的體現(即加強筋、不規則邊緣、干涉情況約束等), 分析并建立了工藝約束在廣義層面上的約束數學模型(如式(1)所示),考慮了約束的所有類型(即等式約束、不等式約束、不連續定義區間約束、離散定義域約束). 因此, 本文提出的修補算法和改進的遺傳算法具有較廣泛的適用性, 能用于所有包含等式、不等式、離散定義區間和定義域的約束優化問題. 如圖11所示, 本文的改進遺傳算法用于機身前端框件的案例, 該框件具有更復雜的不規則邊緣. 由形變云圖可見, 本文的改進遺傳算法適用于此零件, 該框件在優化后的支撐序列下的形變量得到了改善.

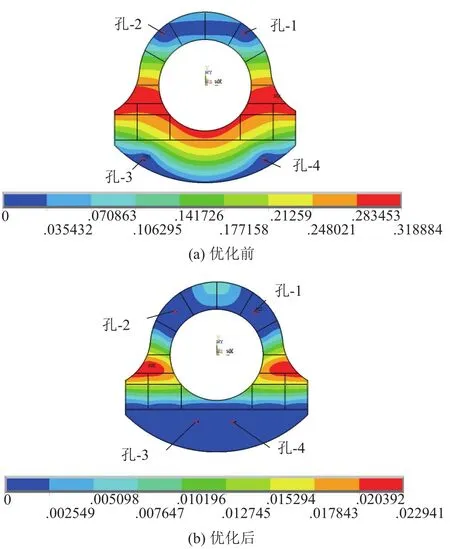
圖10 優化前后形變量云圖

圖11 機身前端框件優化前后形變量云圖

4 結論

(1) 本文將飛機機身框件因變形而引起的柔性定位誤差作為優化目標, 建立相應的優化數學模型, 對可重構工裝的支撐序列進行優化. 框的形變誤差減小93.08%, 提升了可重構柔性工裝在飛機裝配中的精度,推進了先進可重構柔性工裝在制造領域的應用.

(2) 從實際工程問題出發, 針對框的支撐/定位序列優化中的工藝特征約束, 提出一種修補算法, 并基于該算法改進遺傳算法. 改進的遺傳算法保證了種群中個體導入有限元分析軟件中運行的可行性, 保證了優化算法的穩定性, 有效地彌補了其他約束處理技術在處理工藝特征約束問題時的缺陷.

(3) 從工藝特征約束的本質出發, 建立工藝特征約束的廣義數學模型, 基于數學模型提出修補算法及改進的遺傳算法, 具有一定通用性, 能夠用于其他約束優化問題.

1馮子明, 鄒成, 劉繼紅, 等. 飛機關鍵裝配特性的識別與控制. 計算機集成制造系統, 2010, 16(12): 2552–2556.

2齊振超, 張開富, 李原, 等. 大型壁板自動鉆鉚定位誤差分析與優化. 航空學報, 2015, 36(10): 3439–3449.

3郭飛燕, 王仲奇, 康永剛, 等. 飛機立柱式柔性工裝定位誤差分析與精度保障. 計算機集成制造系統, 2013, 19(8):2036–2042.

4王勇, 蔡自興, 周育人, 等. 約束優化進化算法. 軟件學報,2009, 20(1): 11–29.

5MEZURA-MONTES E, Coello CAC. Constraint-handling in nature-inspired numerical optimization: Past, Present and Future. Swarm and Evolutionary Computation, 2011, 1(4):173–194. [doi: 10.1016/j.swevo.2011.10.001]

6KRAMER O. A review of constraint-handling techniques for evolution strategies. Applied Computational Intelligence and Soft Computing, 2010, (11): 1–11.

7BARBOSA HJC, LEMONGE ACC: An adaptive penalty method for genetic algorithms in constrained optimization problems. INTECH: Open Access Publisher, 2008: 9–34.

8HO PY, SHIMIZU K. Evolutionary constrained optimization using an addition of ranking method and a percentage-based tolerance value adjustment scheme. Information Sciences,2007: 2985–3004.

9DEB K, SRIVASTAVA S. A genetic algorithm based augmented Lagrangian method for constrained optimization.Computational Optimization and Applications, 2012, 53(3):869–902. [doi: 10.1007/s10589-012-9468-9]

10MONTEMURRO M, VINCENTI A, VANNUCCI P. The automatic dynamic penalisation method(ADP) for handling constraints with genetic algorithms. Computer Methods in Applied Mechanics and Engineering, 2013, 256: 70–87. [doi:10.1016/j.cma.2012.12.009]

11王俊年, 劉云連, 伍鐵斌. 改進的約束優化多目標遺傳算法及工程應用. 計算機工程與應用, 2015, 51(3): 247–253.

12TAKAHAMA T, SAKAI S. Constrained optimization by applying the α constrained method to the nonlinear simplex method with mutations. IEEE Trans. on Evolutionary Computation, 2005, 9(5): 437–451. [doi: 10.1109/TEVC.2005.850256]

13林丹, 李敏強, 寇紀淞. 基于遺傳算法求解約束優化問題的一種該算法. 軟件學報, 2001, 12(4): 628–632.

14王曉圓, 王愛民, 范瑞城, 等. 基于遺傳算法的配作齊停類調度約束處理技術. 計算機集成制造系統, 2014, 20(11):2788–2797.

15甘敏, 彭輝, 王勇. 多目標優化與自適應懲罰的混合約束優化進化算法. 控制與決策, 2010, 25(3): 378–382.

16ZHANG C, LI X, GAO L, et al. An improved electromag-Lnetism-like mechanism algorithm for constrained optimization. Expert Systems with Applications, 2013, 40(14): 5621–5634. [doi: 10.1016/j.eswa.2013.04.028]

17李維亮, 楊京京, 周良明. 基于模塊化設計的柔性裝配工裝關鍵技術研究. 機床與液壓, 2016, 44(4): 14–17.

18郭飛燕, 王仲奇, 康永剛, 等. 基于坐標孔的翼肋柔性裝配協調方法. 中國機械工程, 2014, 25(24): 3271–3277. [doi:10.3969/j.issn.1004-132X.2014.24.002]

19田威, 廖文和, 唐金成. 面向復雜產品裝配的柔性工裝共性技術研究. 中國機械工程, 2010, 21(22): 2699–2704.

20張洪雙, 蔣君俠, 柯映林, 等. 用于大部件調姿的數控定位器布局及行程優化. 計算機集成制造系統, 2013, 19(11):2742–2747.

21金棟平, 紀斌. 機翼后緣柔性支撐結構的拓撲優化. 航空學報, 2015, 36(8): 2681–2687.

22蓋宇春, 朱偉東, 柯映林. 大型飛機總裝配中支撐點設計分析技術. 浙江大學學報(工學版), 2013, 47(12): 2176–2183.

23XIONG L, MOLFINO R, ZOPPI M. Fixture layout optimization for flexible aerospace parts based on selfreconfigurable swarm intelligent fixture system. International Journal of Advanced Manufacturing Technology, 2013,66(9-12): 1305–1313. [doi: 10.1007/s00170-012-4408-5]

24LU C, ZHAO H W. Fixture layout optimization for deformable sheet metal workpiece. The International Journal of Advanced Manufacturing Technology, 2015, 78(1): 85–98.

Improved Genetic Algorithm Based on Process Constraint

ZHANG Jie, SHEN Jian-Xin, TIAN Wei
(College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

To improve the accuracy and eliminate the error of aircraft assembly, the fixture layout for aircraft frame component with complicated process feature is optimized. In terms of process constraints, a generalized mathematical model of constraints is constructed and a theoretical repairing method is proposed. Additionally, an improved Genetic Algorithm is proposed based on the repairing method. In the example of fixture layout optimization of reconfigurable flexible fixture for frame component, the improved algorithm performed stably and the flexible position error, as a consequence, had reduced dramatically, at around 93.08%. The theoretical analysis and simulation result show that the improved Genetic Algorithm adapts to various kinds of constraint optimization and is feasible for its fast convergence rate and stability.

assembly precision; Genetic algorithm; constraint optimization; repairing method; process constraint; aircraft assembly

張節,沈建新,田威.基于工藝特征約束的改進遺傳算法.計算機系統應用,2017,26(7):245–251. http://www.c-s-a.org.cn/1003-3254/5846.html

國家科技重大專項(2014ZX04001071)

2016-10-31; 收到修改稿時間: 2016-12-05