基于事件觸發的廣義網絡控制穩定性分析

阿如罕++趙立英+白敬

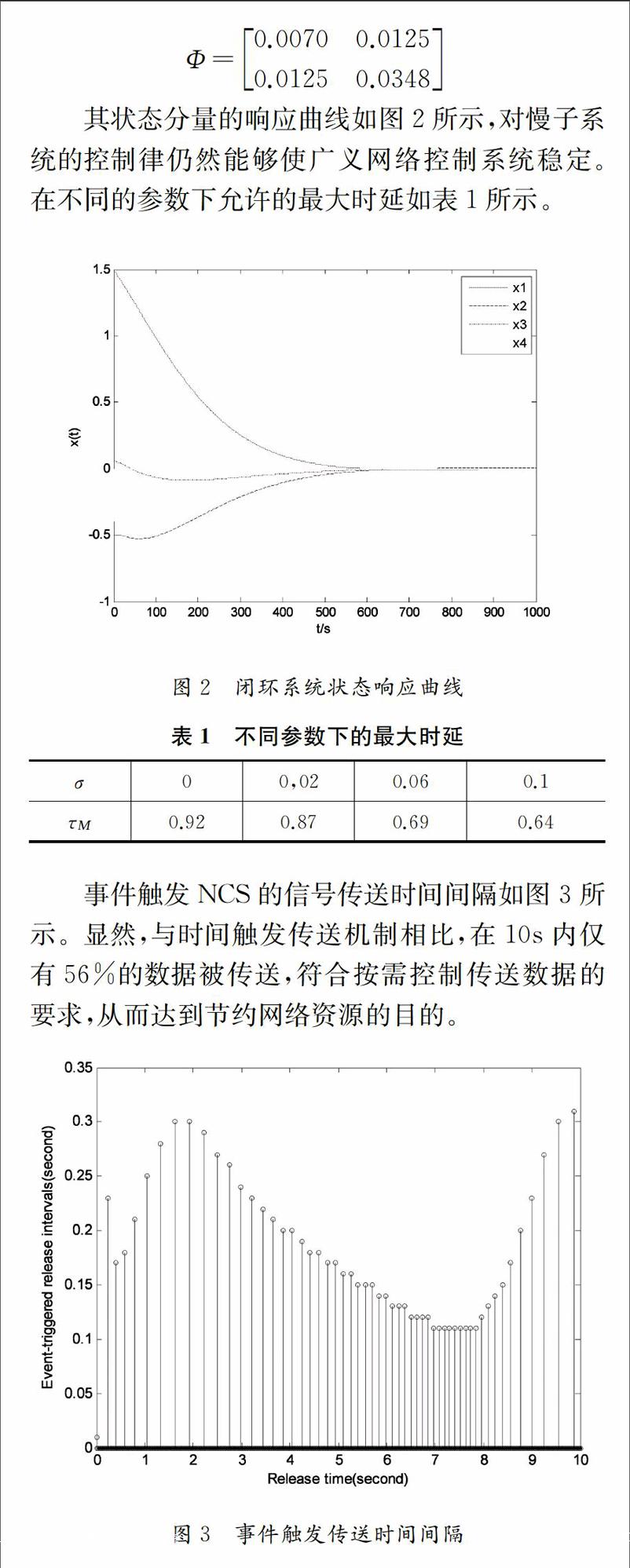
摘 要：本文以廣義系統為被控對象，對一類廣義網絡控制系統進行等價受限變換，通過建立慢子系統的狀態反饋控制使系統達到漸進穩定。進一步給出了在事件觸發機制下的系統穩定性條件。基于該穩定性判據，得到了輸出反饋控制器的設計方法，數值仿真結果表明了該方法的有效性。

關鍵詞：廣義網絡控制系統；事件觸發；線性矩陣不等式

中圖分類號：TP273 文獻標識碼：A

Abstract： In this paper，the controlled plant is singular system，and the singular networked control systems equivalent conversion is given. By estabilish the state feedback control of slow subsystem to guarantee the singular networked control systems stable. Moreover，a event-triggered communication scheme is proposed and the corresponding state feedback controller is designed. Finally，an practical example is given to show that the effectiveness and the feasibility of proposed approach.

Key words： Singular networked control systems； Event-triggered； Linear matrix inequality

1.引言部分

網絡控制系統NCS（networked control system，NCS）是通過網絡形成的反饋控制系統。其中被控對象、傳感器、控制器和執行器可以分布在不同的物理位置，由一個公共的網絡平臺完成信息交換，形成一種實時反饋閉環控制系統[1]。這種網絡化的控制模式與傳統的控制相比不僅能夠實現共享信息資源，減少連接線數而且具有易于擴展、易于維護、高效率、高可靠性及靈活等優點[2-3]。

近年來，有關NCS的分析與綜合方面的研究受到了國內外學者的廣泛關注。雖然網絡控制系統有很多優越性，但是網絡環境的影響是無法忽略的。針對網絡帶寬有限的情況專家學者提出了事件觸發機制[4-6]，即每個采樣數據都需要經過事件觸發條件的篩選，滿足條件的采樣可以經過網絡傳輸到控制器，而不滿足條件的信號會被直接舍棄。這樣可以保證閉環系統具有一定穩定性能的情況下與以往的時間觸發方式相比更加有效地節約網絡資源。

但目前的研究廣泛關注正常的網絡控制系統，考慮被控對象為廣義系統的并不多見。廣義系統又稱為奇異系統，它是一類涵蓋正常系統的更具一般化的動力系統[7]。在對廣義系統進行研究時，不僅要保證廣義系統在時間域 是穩定的，還要研究它的解在時間域 是正則的、無攝動的[8]。

文獻[9]以廣義系統為被控對象的NCS為模型，考慮了系統的時延以及丟包，根據受限等價變換給出了系統的離散化形式，但是傳感器、控制器和執行器是時間觸發，并沒有考慮事件觸發。文獻[10]對廣義網絡控制引入事件觸發機制，首先根據已給出的穩定性條件判斷系統正則、無脈沖，以此來保證系統有唯一解。其次在構造Lyapunov函數時與以往的正常系統時不同，考慮了奇異矩陣E。

本文以廣義系統為被控對象，對其進行等價受限變換，給出了在事件觸發機制下的系統穩定性條件。首先建立了在慢子系統的狀態反饋控制下的廣義網絡控制系統新模型，通過其構造新的Lyapunov函數，引入適當的自由權矩陣，利用線性矩陣不等式與穩定性理論，得到系統漸進穩定的條件。基于已獲得的穩定性的條件，提供了一種狀態輸出反饋控制器設計的方法。

2 問題描述

4 結 論

本文研究了一類廣義網絡控制系統的穩定性與控制器設計。針對廣義系統的特點通過受限等價變換引入對慢子系統的控制律使得系統達到穩定。在數據傳送機制上采取事件觸發機制，與文獻[9]相比大大減少了數據傳輸量，同時又能夠保持良好的穩定性。仿真結果表明了該方法的有效性。

參考文獻

[1] 岳東， 彭晨. 網絡控制系統的分析與綜合 [M]. 科學出版社， 2007.

[2] Yue Dong， Tian En gang， and Han Qing Long. A Delay System Method for Designing Event-Triggered Controllers of Networked Control Systems[J]. Automatic Control， IEEE Transactions on. 2013， vol. 58 ：475-481.

[3] Peng Chen， Yang Tai Cheng. Event-triggered communication and H∞ control co-design for networked control systems[J]. Automatic， 2013， 49（5）： 1326-1332.

[4] Hu Song Lin， Yue Dong. Event-triggered control design of linear networked systems with quantizations[J]. ISA transactions， 2012， 51（1）： 153-162.

[5] Zha Liu Juan， Fang Jian An， Liu Jin Liang. Two channel event-triggering communication schemes for networked control systems[J].Neurocomputing， 2016， 197：45-52.

[6] 李煒， 趙莉， 蔣棟年. 基于事件觸發的 NCS 魯棒完整性設計[J]. 蘭州理工大學學報， 2014， 40（1）： 74-79.

[7] 劉麗麗， 張慶靈， 杜昭平. 時延廣義網絡控 制系統的建模與分析[J]. 東北大學學報，自然科學版， 2011， 32（2）：172-174.

[8] Lewis F L. A survey of linear singular systems[J]. Circuits Systems & Signal Processing， 1986， 5（1）：3-36.

[9] Liu Li Li， Li Jing Hao， Zhang Qing Ling， et al. The controller design for singular networked control system with delay and data packet dropout[C]. The 26th Chinese Control and Decision Conference （2014 CCDC）. 2014.

[10] Wang Hui jiao， Ying Yu jia， Lu R， et al. Network-based H∞ control for singular systems with event-triggered sampling scheme[J].Information Sciences， 2016，329： 540-551.

[11] 楊冬梅， 張慶靈姚波等. 廣義系統[M]. 科學 出版社， 2008.

[12] Shi Peng， Wang Hui jiao， Lim Chen Chew. Network-based event-triggered control for singular systems with quantizations[J]. IEEE Transactions on Industrial Electronics， 2016， 63（2）： 1230-1238.