固定鴨舵控制誤差對修正彈落點散布的影響

黃 偉，高 敏，王 毅，方 丹

(解放軍軍械工程學院，河北 石家莊 050003)

固定鴨舵控制誤差對修正彈落點散布的影響

黃 偉，高 敏，王 毅，方 丹

(解放軍軍械工程學院，河北 石家莊 050003)

針對不同控制誤差條件下彈丸的落點散布規律，分析了控制誤差的表現形式，將控制誤差近似描述為均值誤差和抖動誤差兩項之和，設計了基于七自由度彈道模型的蒙特卡洛打靶仿真實驗，得到了不同誤差條件下修正彈的落點散布。仿真結果表明，固定鴨舵滾轉角控制均值誤差和固定鴨舵抖動誤差都會增大修正彈落點散布，降低命中精度，且固定鴨舵抖動產生的影響大于控制均值誤差的影響。該項研究可為固定鴨舵式二維彈道修正彈控制算法優化提供依據。

固定鴨舵；控制誤差；落點散布

0 引言

炮彈通過安裝彈道修正引信，能夠有效減小彈丸散布，提高命中精度[1]。固定鴨舵式二維彈道修正組件是當前彈道修正引信研究的熱點。國內外學者針對固定鴨舵式二維彈道修正組件總體技術、彈道建模、氣動特性和控制算法進行了大量研究。

最早關于固定鴨舵式修正組件的描述見于J. A. Clancy，T. D. Bybee所申請的專利[2]中，通過頭部減旋的方式實現了固定鴨舵單通道控制，提供了一種解決高轉速旋轉穩定彈控制難題的方法。M. Costello基于傳統六自由度剛體彈道模型，考慮修正組件和彈體滾轉角不同帶來的差異，建立了七自由度剛體彈道模型[3]。郝永平等[4]研究了固定鴨舵參數對彈丸氣動特性的影響。紀秀玲等[5]采用數值模擬的方法分析了鴨舵方位角對彈丸俯仰特性的影響規律。P. Wernert采用線性化理論分析了155 mm旋轉穩定彈的穩定性[6]。固定鴨舵的控制方面，文獻[7-8]分別采用PID控制算法和模糊控制算法設計了固定鴨舵滾轉控制器，實現了固定鴨舵滾轉角的單通道控制。受彈丸實際飛行過程中外部干擾和彈體參數變化的影響，固定鴨舵的滾轉控制存在誤差。研究固定鴨舵滾轉角控制誤差對落點散布的影響規律，對于改進控制算法、改善落點散布、提高命中精度具有十分重要的意義。國內外關于固定鴨舵的控制誤差對彈丸落點散布和命中精度的影響研究，尚未見于公開報道。本文針對不同控制誤差條件下彈丸的落點散布規律展開研究。

1 固定鴨舵控制誤差描述

1.1 固定鴨舵控制原理

固定鴨舵式二維彈道修正組件由固定鴨舵、雙轉式直流電機、衛星接收機、彈載計算機、地磁組件、慣性元件等部分組成。固定鴨舵由一對同向舵和一對反向舵組成，一對同向舵產生空氣導轉力矩，一對反向舵產生垂直于其連線的修正力。

固定鴨舵式二維彈道修正組件的工作過程[9-10]為：彈丸發射后，來流作用于一對同向舵產生導轉力矩，驅動固定鴨舵相對彈體反向旋轉；彈道測量部件實時測量彈丸飛行彈道諸元，交由彈載計算機預測落點、計算彈道誤差，當落點誤差達到控制系統設定閾值時，啟動彈道修正控制并解算目標滾轉角；地磁組件實時測量固定鴨舵滾轉角位置，慣性元件測量固定鴨舵滾轉角速度；電機驅動控制單元根據實測滾轉角位置、目標滾轉角位置和滾轉角速度，驅動電機產生制動力矩使固定鴨舵減速并最終停留在目標滾轉角位置。此時一對反向舵產生的修正力作用于彈丸，使彈丸姿態發生變化，改變彈體受力從而實現彈道修正。

固定鴨舵控制是修正組件實現彈道修正的關鍵。在固定鴨舵控制時，直流電機提供制動力矩以克服同向舵導轉力矩、軸承摩擦力矩和阻尼力矩的合力矩作用，使反向舵穩定在相應的目標滾轉角位置。當滾轉角控制出現超調時，需要快速減小制動力矩，使固定鴨舵在合力矩作用下保持相對彈體反旋，并最終穩定在目標滾轉角。

本文采用PID控制算法，其控制系統如圖1所示。分別通過地磁組件和慣性元件采集當前角位置和角速度，用目標滾轉角和實測滾轉角計算出一個角度差值，用于PID控制的比例環節和積分環節，角速度反饋用作微分環節，構成基本的PID控制算法。

1.2 固定鴨舵控制誤差的近似描述

在固定鴨舵的實際控制過程中，由于控制算法精度有限，加上外部干擾和固定鴨舵參數變化的影響，固定鴨舵不能精確停留在目標滾轉角上，存在控制誤差，從而影響落點散布和射擊精度。

為了準確描述固定鴨舵控制誤差，設計一個目標滾轉角為0°的地面實驗。通過研究固定鴨舵滾轉角控制在0°時的滾轉角控制誤差表現形式，得出控制誤差的近似描述。

圖2為地面實驗中光電碼盤測得的固定鴨舵滾轉角曲線。圖中，在8～12 s控制時段內，固定鴨舵滾轉角以誤差均值為中心做往復振蕩運動。因此可以將滾轉角控制誤差分解為均值誤差和抖動誤差兩項進行分析。

為便于研究不同控制誤差分量對修正彈落點散布的影響，根據兩項誤差的表現形式，用如下表達式來近似描述固定鴨舵控制誤差：

y=yA+yB

(1)

式中，yA=Asin(ωt+φ0)為滾轉角抖動誤差，A為滾轉角振幅，ω為固定鴨舵抖動的角頻率，φ0為相位角；yB為滾轉角誤差均值，此處定義其為平均值為B1、標準差為B2的隨機數yB=rand(B1，B2)。

在前述目標滾轉角為0°的地面實驗中，A= 0.5°，ω=2π rad/s，B1=0.5°，B2=0.2°，φ0=π/3 rad，得到的6～12 s控制誤差近似描述曲線如圖3所示。在仿真實驗中用該近似描述曲線代替控制誤差。

2 固定鴨舵控制誤差對落點散布的影響

為了研究固定鴨舵控制誤差對落點散布的影響規律，需要設計仿真實驗。仿真實驗的設計要解決如下三個問題：一是建立修正彈彈道模型，二是確定控制誤差的表達式，三是采用合適的修正彈落點散布的仿真方法。

2.1 固定鴨舵式彈道修正彈彈道模型

關于固定鴨舵式二維彈道修正彈的彈道建模問題，王毅等針對單通道磁力矩電機控制模式，基于修正組件與彈體無氣動耦合假設，將固定鴨舵相對彈體反旋看作彈丸運動的第七個自由度，建立起固定鴨舵二維彈道修正彈七自由度彈道模型[11]。本文的研究中，選擇該七自由度彈道模型作為仿真模型，如式(2)—式(5)所示。

(2)

彈丸繞質心的角運動方程為：

(3)

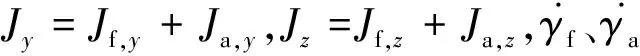
彈丸的質心運動方程為：

(4)

彈丸角運動方程為：

(5)

式中，φ，ψ為修正組件的俯仰角和偏航角。

2.2 固定鴨舵控制誤差設置

假設在實際飛行條件下，固定鴨舵控制誤差仍然與前節推導的表達式具有相同形式。考慮實際飛行過程中有非恒定的空氣力矩作用、地磁測量滾轉角在實際飛行過程中受電磁干擾等復雜環境影響會有較大偏差以及制動控制容許不大于10°的偏差等因素，實際滾轉角振幅和滾轉角均值誤差與地面實驗相比較大。為了保證實驗結果的有效性，仿真中選擇較大的誤差值，本文中取A=5°，B1=5°，B2=1°，ω=2π rad/s，φ0=π/3 rad。即取定固定鴨舵控制誤差表示為：

y=5sin(2πt+π/3)+rand(5,1)

(6)

2.3 修正彈落點散布仿真方法

修正彈在飛行過程中受到多種干擾，在研究固定鴨舵控制誤差對彈丸落點散布時，統一將其他干擾視為服從正態分布的隨機干擾。基于以上假設，本文采用蒙特卡洛模擬打靶[12]進行落點散布研究。蒙特卡洛模擬打靶是一種統計實驗法，其基本思想是利用計算機的數值模擬來代替飛行試驗，通過大量仿真研究系統統計意義下的特性。此方法已廣泛應用在研究環境因素和系統誤差對射擊精度的影響實驗研究[13]中，流程圖如圖4所示。

3 模擬仿真實驗及結果分析

通過前文的誤差分析可知，固定鴨舵滾轉角控制誤差分為兩部分，即控制角度均值誤差和固定鴨舵抖動誤差。因此，本文研究控制誤差對彈丸落點散布的影響，進行以下四組模擬打靶實驗：1)無滾轉控制控制誤差打靶實驗；2)加均值誤差打靶實驗；3)加固定鴨舵抖動打靶實驗；4)加綜合誤差打靶實驗。每組實驗分有控和無控兩種模式各模擬打靶100次。

進行無控打靶實驗，一是為了與有控打靶結果對比，驗證固定鴨舵有效控制能夠實現彈道修正；二是為了驗證七自由度彈道模型和模特卡洛打靶方法的正確性。

無滾轉控制誤差打靶實驗結果如圖5所示，落點的縱向誤差標準差為23.95m，橫向誤差標準差為24.69m，CEP為28.62m。無控打靶結果在目標點附近隨機分布，沒有異常落點，證明本文采用的七自由度彈道模型和模特卡洛打靶方法正確；有控與無控打靶結果對比可知，固定鴨舵的有效控制能夠減小彈丸落點散布，提高射擊精度。

加均值誤差打靶實驗結果如圖6所示。添加均值誤差后，彈丸的縱向散布和橫向散布略有增大，縱向偏差標準差為24.54m，橫向偏差標準差為25.22m，分別增大了0.59m和0.53m；落點CEP為29.11m，增大了0.49m。

圖7是加固定鴨舵抖動打靶實驗結果。固定鴨舵抖動降低了控制效率，導致修正能力未能充分發揮。落點的縱向散布和橫向散布均增大，縱向偏差標準差為25.37m，橫向偏差標準差為27.04m，分別增大了1.32m和2.33m。落點CEP為30.42m，增大了1.80m。

圖8是加綜合誤差打靶實驗結果。添加綜合誤差后，落點的縱向和橫向散布略有增大。縱向偏差標準差為25.59m，橫向偏差標準差為27.77m，分別增大了1.64m和3.08m；CEP為30.99m，增大了2.37m。

以上蒙特卡洛打靶實驗結果如表1所示。

對比不同誤差條件下的結果，能夠得到以下結論：

1)均值誤差、抖動誤差和綜合誤差打靶結果與無滾轉控制誤差打靶結果比較可知，控制誤差的存在，會導致彈丸落點散布變大，命中精度降低。

2)均值誤差、抖動誤差打靶結果與無滾轉控制誤差打靶結果比較可知，控制角均值誤差和固定鴨舵抖動誤差均會增大修正彈落點散布，降低命中精度。綜合誤差打靶結果與單一誤差打靶結果比較同樣可驗證上述結論。

3)綜合誤差打靶結果與均值誤差、抖動誤差打靶結果比較說明控制角均值誤差與固定鴨舵抖動誤差對落點散布的影響趨勢是相同的，即均會增大修正彈的落點散布。

4)均值誤差打靶結果與抖動誤差打靶結果對比可知，固定鴨舵抖動對落點散布的影響較大，均值誤差對落點散布的影響較小。

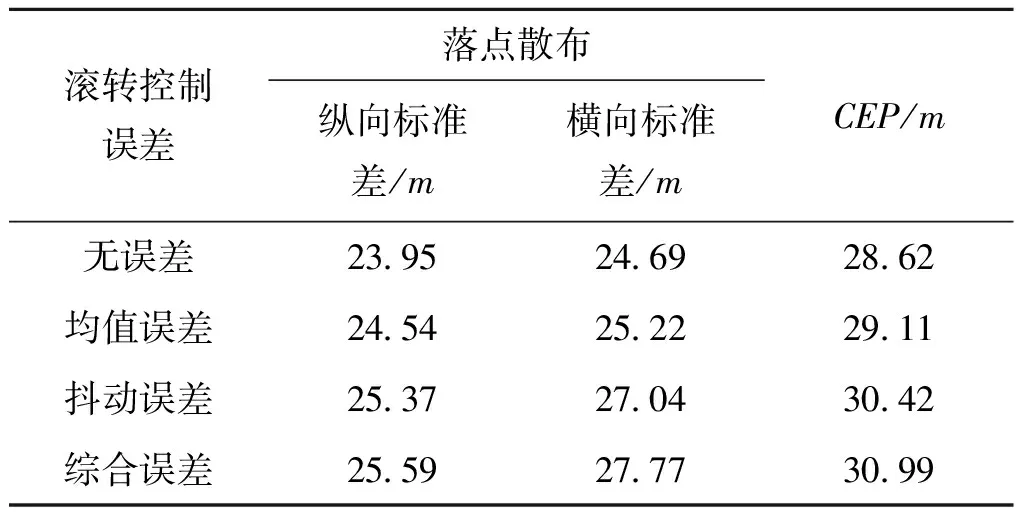
表1 打靶實驗結果

上述仿真實驗結論表明，在固定鴨舵控制系統設計中，要通過改進算法等措施使控制角均值誤差和固定鴨舵抖動盡量小，以使修正彈落點散布更集中，命中精度更高；在無法同時使控制角均值誤差和固定鴨舵抖動達到最小要求時，可適當放寬對均值誤差的限制，盡量抑制固定鴨舵的抖動。

4 結論

對于固定鴨舵式二維彈道修正彈而言，固定鴨舵控制誤差將會影響修正彈落點散布和命中精度。本文首先分析了固定鴨舵控制誤差的形成原因，并通過目標滾轉角為0°的地面實驗得到了控制誤差的近似描述。然后基于七自由度彈道模型進行蒙特卡洛打靶實驗，分別加入均值誤差、固定鴨舵抖動誤差和綜合誤差，研究不同誤差條件下落點散布和命中精度。仿真結果表明，固定鴨舵控制誤差會增大修正彈的落點散布，降低其命中精度；固定鴨舵抖動誤差比均值誤差對落點散布的影響更大。這為固定鴨舵控制策略的制定和控制算法的優化提供了依據，具有一定工程實際意義。

[1]馬寶華. 網絡技術時代的引信[J]. 探測與控制學報, 2006, 28(6):1-5.

[2]ClancyJA,BybeeTD,FridrihW.Fixedcanard2-Dguidanceofartilleryprojectile[P].US: 6981672B2, 2006-01-03.

[3]CostelloM.Modelingandsimulationofdifferentialrollprojectile[C]//ModelingandSimulationTechnologiesConference.Boston:AIAA, 1998:490-499.

[4]郝永平, 孟慶宇, 張嘉易. 固定翼二維彈道修正彈氣動特性分析[J]. 彈箭與制導學報, 2012, 32(3):171-173.

[5]紀秀玲, 王海鵬, 曾時明. 可旋轉鴨舵對旋轉彈丸氣動特性的影響[J]. 北京理工大學學報, 2011, 31(3):265-268.

[6]WernertP.Stabilityanalysisforcanardguideddual-spinstabilizedprojectiles[C]//AtmosphericFlightMechanicsConference.Chicago:AIAA, 2009:1-24.

[7]高銘澤, 施坤林, 霍鵬飛，等. 引信滾轉角雙閉環控制算法[J]. 探測與控制學報, 2013, 35(3):17-20.

[8]楊愷華, 祁克玉, 王芹. 基于模糊控制的二維彈道修正引信滾轉角控制算法[J]. 探測與控制學報, 2015, 37(2):19-23.

[9]吳萍, 陳少松, 楊晉偉，等. 旋轉控制固定鴨舵二維彈道修正彈氣動特性[J]. 彈道學報, 2014, 26(3):6-10.

[10]張衍儒, 肖練剛, 張繼生. 旋轉控制固定鴨舵的導航初始化與控制算法研究[J]. 航天控制, 2014, 32(6):34-39.

[11]王毅, 宋衛東, 佟德飛. 固定鴨舵式彈道修正彈二體系統建模[J]. 彈道學報, 2014, 26(4):36-41.

[12]王志剛, 李偉. 滾轉隔離結構制導火箭彈蒙特卡洛法仿真研究[J]. 計算機仿真, 2012, 29(11):99-103.

[13]王華, 徐軍, 張蕓香. 基于Matlab的彈道蒙特卡洛仿真研究[J]. 彈箭與制導學報, 2005, 25(1):181-183.

Influence of Fixed Canard Control Error on Dispersion of Trajectory Correction Projectile

HUANG Wei, GAO Min, WANG Yi, FANG Dan

(Ordnance Engineering College of PLA, Shijiazhuang, 050003, China)

To study the dispersion of trajectory correction projectiles in different control error conditions, the form of control error was analyzed and the error was described as a sum of mean component and dithering component. Monte Carlo simulation based on 7-degree of freedom trajectory model was designed to obtain the dispersion under different error conditions. The results showed that the control error could increase the dispersion and reduce the hit accuracy, and the dithering component had greater effect on dispersion than the mean component.

fixed canards; control error; dispersion

2016-12-07

武器裝備預研基金項目資助(9140A05040114JB34015)

黃偉(1991—)，男，土家族，湖北恩施人，碩士研究生，研究方向：彈箭智能與信息化。E-mail:buaahuangwei@126.com。

TJ412.3

A

1008-1194(2017)03-0070-05