小口徑火炮彈頭觸發引信機械零件質量散布特性

劉 鵬，王雨時，聞 泉，張志彪

(南京理工大學機械工程學院，江蘇 南京 210094)

小口徑火炮彈頭觸發引信機械零件質量散布特性

劉 鵬，王雨時，聞 泉，張志彪

(南京理工大學機械工程學院，江蘇 南京 210094)

為了找出引信機械零件質量散布特性規律，從而提高引信產品工程設計質量、安全性和可靠性，以小口徑航炮彈頭觸發引信和高炮彈頭觸發引信為樣本，利用數理統計方法獲得了其機械零件質量散布特性。這兩種引信零件質量總的散布特性規律相近；約有半數品種的零件質量散布服從正態分布或Weibull分布；還有約50%的零件種類不服從典型分布；結構維數越多，零件的質量散布越大；無表面處理的零件質量散布較大；平均尺寸精度等級對零件散布特性影響不明顯，每降低一個等級，零件質量散布約增大0.5%。

引信；數理統計；零件質量；散布特性

0 引言

引信發射時所受過載最大可達十幾萬g，零部件質量變化對其后坐力影響較大，進而影響發射強度和后坐(慣性)保險機構解除保險可靠性[1]，因此研究引信零部件的質量散布特性對于確保產品工程設計質量、提高引信安全性和可靠性具有重要意義。對于極少數簡單幾何形狀的零件，因其材料密度變化不大，理論上可以采用全微分方式求出其質量散布受尺寸誤差影響的數學關系式。但對絕大多數的零件，由于組合后的幾何形狀過于復雜，所以工程實踐上多用數理統計的方法來研究其質量散布特性[2]。文獻[3]以小口徑高炮彈頭觸發引信機械零件為例，利用數理統計方法，獲得了其機械零件質量散布特性與由這些機械零件隨機組合而成的引信產品質量散布特性，但由于積累數據較少，樣本量小，未得到明顯散布特性。本文在文獻[3]研究的基礎上，加大實測質量數據樣本量開展研究，試圖進一步找出引信機械零件質量散布特性規律。

1 分析方法與樣本概況

1.1 分析方法

非參數檢驗是統計分析方法的重要組成部分，它與參數檢驗共同構成統計推斷的基本內容。非參數檢驗是在總體分布未知或知道甚少的情況下，根據來自總體的樣本對總體的分布進行推斷，并利用樣本數據對總體分布形態等進行推斷的方法。

常用的非參數檢驗方法有卡方檢驗、二項分布檢驗、K-S檢驗以及變量值隨機性檢驗等方法。K-S檢驗方法能夠利用樣本數據推斷樣本來自的總體是否服從某一理論分布，是一種擬合優度的檢驗方法，適用于探索連續型隨機變量的分布。一般認為K-S檢驗法可直接處理原始數據，且在樣本不大時也可使用[4-6]。本文利用Matlab自帶工具箱直接對各樣本進行參數估計，并選擇K-S檢驗法對所得參數進假設檢驗[7-8]。

1.2 樣本概述

以一種小口徑航炮引信18種機械零件和6種部件的合格品各200件稱重數據為樣本，零件質量均值、標準差和極值如表1所列，頻數分布直方圖如圖1所示；部件質量均值、標準差和極值如表2所列，頻數分布直方圖如圖2所示。

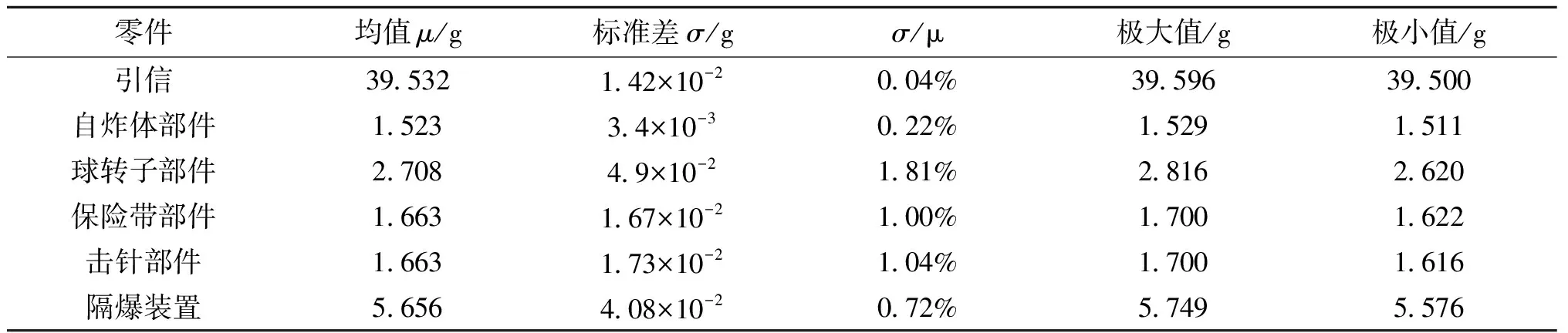
表2 各部件質量均值、標準差和極值

2 參數估計和分布擬合

據前人研究，分別對各零件質量散布進行正態分布假設和Weibull分布假設，并進行參數估計和分布擬合檢驗。各零件質量散布擬合參數如表3所列；零件特征和散布檢驗結果如表4所列，其中尺寸數大于4的零件，其平均尺寸精度等級為前4個最大尺寸的精度等級均值四舍五入后取整數；各部件質量散布擬合參數如表5所列，部件特征和散布檢驗結果如表6所列。

表3 各零件質量散布參數

續表

零件名稱正態分布Weibull分布均值μ/g標準差σ/gσ/μ形狀參數a尺度參數b壓桿3 739×10-26 979×10-41 87%3 771×10-262 365Φ2 5mm鋼球6 217×10-22 290×10-40 37%6 227×10-2365 421擊針0 1653 102×10-31 88%0 16670 151保險帶1 6943 611×10-30 21%1 696464 603簧圈3 619×10-22 118×10-30 59%3 728×10-212 104下體16 7057 866×10-20 47%16 745199 584墊片0 1391 344×10-29 67%0 14510 450球蓋1 4933 448×10-30 23%1 494548 90球轉子2 6178 851×10-30 34%2 621281 983開口環9 356×10-22 096×10-32 24%9 462×10-242 229壓螺4 2463 735×10-20 88%4 263122 91鋁蓋4 745×10-23 053×10-40 64%4 760×10-2169 50套0 1733 367×10-31 95%0 17550 262支承桿0 6864 669×10-30 68%0 689154 13

表4 各零件特征和散布擬合檢驗結果

表5 各部件質量散布參數

表6 各部件特征和散布擬合檢驗結果

表1和表3中簧圈和墊片兩種零件質量散布較大，簧圈可達±17.5%，墊片可達±28.9%。分析發現其原因分別是：簧圈主要尺寸公差相對值都比較大，如長度為±1.5%、厚度為±10%、寬度為±5%；墊片振動拋光磨去的厚度難以均勻因而散布很大，并且厚度公差相對值已達±6.1%。

由表4可看出，引信的18種機械零件中，自炸體、下體、墊片、開口環和套符合正態分布，壓桿、球蓋符合Weibull分布，支承桿既符合正態分布也符合Weibull分布。由表6可看出，除自炸體部件和球轉子部件無明顯分布特征外，其余部件都符合正態分布，且隔爆裝置部件還符合Weibull分布；部件裝配時微量添加物對部件分布特征無影響。

3 結果分析

為深入分析影響零件質量散布特性的因素，對文獻[3]所涉及的23 mm口徑高炮引信零進行進一步分析，零件特征和散布擬合檢驗結果如表7所列，其中平均尺寸精度等級及含義與表4的相同。

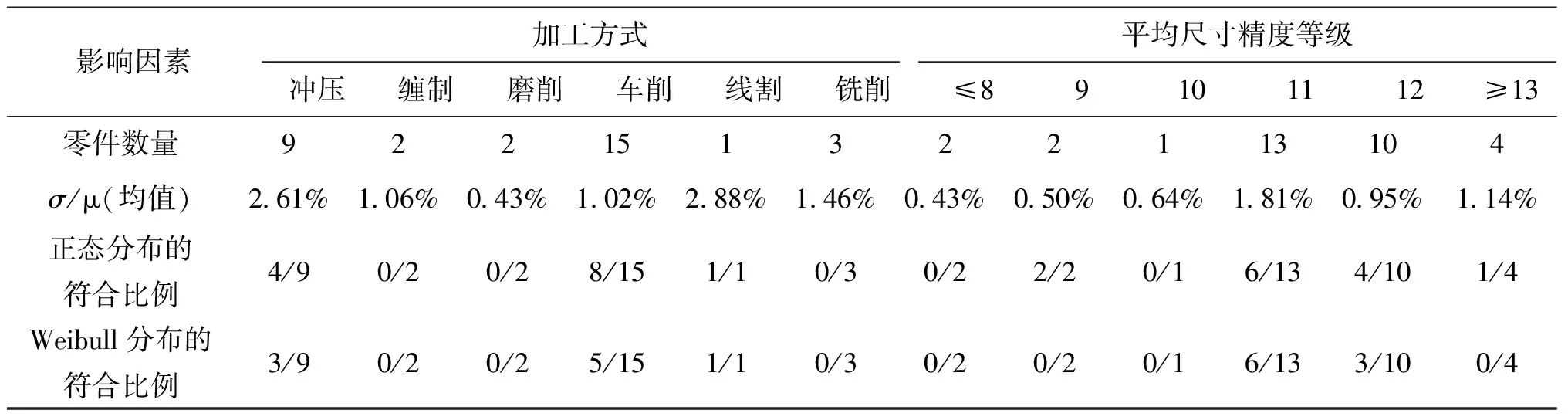
對影響某小口徑航炮引信和23 mm口徑高炮引信零件質量的因素進行統計分析，結果如表8所列。其中23 mm口徑高炮引信零件中的保險銷因質量太小(0.003 g)，測量儀器精度無法區分而無法得到分布類型，未計入統計中。

由表8的統計結果可以看出：

結構維數越多，零件的質量散布越大，服從正態分布和Weibull分布的零件數量比例也越大。結構維數為1的零件(鋼球)質量沒有明顯的分布特性，結構維數為2和3的零件，質量散布特性服從典型散布的比例相近。

零件尺寸越多，零件質量就越符合正態分布或Weibull分布，分布特性越明顯；零件尺寸數對質量散布影響不大。

小質量的零件質量相對散布大。質量小于0.2 g的零件質量散布最大；零件質量散布特性與零件質量關系不大。

密度小的材料加工的零件質量散布較小；材料密度對零件質量散布特性影響不大。

無表面處理的零件質量散布最大，鈍化處理的零件質量散布特性最明顯。

表7 參考文獻[3]中零件質量均值、標準差、極值和散布擬合檢驗結果

表8 兩種小口徑炮彈引信零件質量散布擬合檢驗結果

續表

影響因素加工方式平均尺寸精度等級沖壓纏制磨削車削線割銑削≤89101112≥13零件數量922151322113104σ/μ(均值)2 61%1 06%0 43%1 02%2 88%1 46%0 43%0 50%0 64%1 81%0 95%1 14%正態分布的符合比例4/90/20/28/151/10/30/22/20/16/134/101/4Weibull分布的符合比例3/90/20/25/151/10/30/20/20/16/133/100/4

加工為纏制(彈簧)、磨(保險球)和銑(隔離球)的零件質量無明顯分布特性，而車削與沖壓零件質量散布特性比較明顯，約有二分之一的零件數量服從正態分布，約有三分之一的零件數量服從Weibull分布。

平均尺寸精度等級對質量散布有影響，對表8中平均尺寸精度等級和σ/μ(均值)進行線性擬合，利用最小二乘法得到的回歸曲線方程為：

y=0.1455x-0.7825

式中，x為平均尺寸精度等級，y為σ/μ(均值，%)。

表8表明，平均尺寸精度等級為10級時其質量散布(3σ/μ)約為2%，11級時約為2.5%，12級時約為3%，大約每降低一個等級，零件質量散布約增大0.5%。平均尺寸精度等級對零件散布特性影響不明顯。

4 結論

本文以一種小口徑航炮彈頭觸發引信和一種高炮彈頭觸發引信為樣本，利用數理統計方法獲得了其機械零件質量散布特性。這兩種引信零件質量總的散布特性規律相近；約有半數品種的零件質量散布服從正態分布或Weibull分布；還有約50%的零件種類不服從典型分布；結構維數越多，零件的質量散布越大；無表面處理的零件質量散布較大；平均尺寸精度等級為10級時其質量散布(3σ/μ)約為2%，11級時約為2.5%，12級時約為3%，每降低一個等級，零件質量散布約增大0.5%；平均尺寸精度等級對零件散布特性影響不明顯。

文獻[3]涉及的引信零件為設計階段試驗樣品零件，多由數控機床或加工中心加工。本文涉及的引信零件為已生產定型多年、現處于大批量生產階段的零件，多由普通機床加工。但針對這兩種引信的研究結論并無矛盾之處，說明引信零件質量散布特性規律是相近或相同的。

[1]安曉紅. 引信設計與應用[M]. 北京：國防工業出版社, 2006.

[2]張崇甫. 統計分析方法及其應用[M]. 重慶：重慶大學出版社, 1995.

[3]王曉鵬，王雨時，聞泉，等. 某高炮彈頭觸發引信機械零件質量分布特性[J]. 四川兵工學報，2015，36(5)：63-68.

[4]郭榮化, 李勇. 小樣本試驗中驗前數據與現場數據相容性檢驗方法研究[C]//第13屆中國系統仿真技術及其應用學術年會論文集.合肥：中國自動化學會系統仿真專業委員會, 2011.

[5]王曉鵬，王雨時，盧鳳生，等.155mm口徑火炮榴彈結構特征數分布特性研究[J].探測與控制學報, 2015,37(5):66-72.

[6]宋昕, 蔡泳, 徐剛,等. 非參數檢驗方法概述[J]. 上海口腔醫學, 2004, 13(6):561-563.

[7]王巖. 數理統計與MATLAB工程數據分析[M]. 北京：清華大學出版社, 2006.

[8]劉海波，江健. 基于MATLAB的某型挖掘機可靠性分布模型辨識[J]. 工程機械，2014，45(10):18-23.

The Mass Distribution of Mechanical Components of Small Caliber Artillery’s Point Detonating Fuze

LIU Peng, WANG Yushi, WEN Quan, ZHANG Zhibiao

(Mechanical Engineering School, NUST, Nanjing 210094，China)

In order to find the mass distribution regularity of fuze’s mechanical components,thereby improving product engineering quality, security and reliability of fuze, according to the point detonating fuze of a small caliber aircraft gun and antiaircraft gun, the mass distributions of the components were gained with the method of mathematical statistics.The mass distribution regularity of fuze’s components is similar or same. More than half of the components’ mass obey normal distribution or weibull distribution. There are about half kind of the component are not subject to typical distribution. The more components structure dimension are, the greater the mass spread.Components without surface treatment have greater mass spread. The mass spread (3σ/μ) is about 2% when the average of the dimensional accuracy class at 10, 2.5% at 11 and 3% at 12, the average of the dimensional accuracy class decreasing by a grade,the mass spread of components increased about 0.5%. The average of the dimensional accuracy class has little effect on the mass distribution of components.

fuze; mathematical statistics; components mass; distribution

2016-08-21

武器裝備預先研究項目資助(51305060301)；江蘇省自然科學基金青年基金項目資助(BK20140786)

劉鵬(1991—)，男，湖南長沙人，碩士研究生，研究方向:引信及彈藥總體技術。E-mail：skiy906@163.com。

TJ430.8

A

1008-1194(2017)03-0017-07