基于粒子群算法的水火電力系統負荷優化分配

(三峽大學，湖北 宜昌 443000)

1 引言

電力工業是高耗能產業，提高電力工業能源利用效率，轉變能源利用方式，減少炭基能源使用量，對于緩解我國能源供需矛盾和改善生態環境等具有重要作用。理論及實踐表明，優先利用清潔可再生能源，開展清潔能源與可再生能源的互補運行，是提高電力系統運行經濟，提高能源利用效率和可再生能源的有效途徑。我國目前火電占的比例為67.3%，火電容量將控制在8.9億千瓦左右。因此開展清潔能源與常規炭基能源之間聯合經濟運行的研究具有重要意義。

解決此問題的研究方法有傳統的經典算法和智能算法。傳統的經典算法又以動態規劃規劃算法及其改進為代表，如離散微分動態規劃算法，逐次逼近動態規劃算法，增量動態規劃算法，逐步優化算法等。智能算法有遺傳算法及其改進，粒子群算法，差分進化算法及其改進。

早由Howson和Sancho于1975年提出，它是在動態規劃的思想上，運用最優化原理求解多狀態的動態規劃。它是每兩個階段的決策相對其始端決策和終端決策是最優的。POA法應用于水庫群的優化調度問題時[1]，可以先將水庫群分成多個單水庫系統，對每一個水庫進行優化，以此作為整個水庫群優化問題的最初解，然后再考慮水庫群聯合運行，逐步改進優化策略，如果對于梯級水庫群，也可以把梯級水庫群作為一個整體，在兩階段里自上而下逐一尋優；如果是混聯系統，尋優應從調節最不好的小水庫開始。當然，除了POA算法較好的全局收斂性，計算易實現以外，算法對初值的依賴性是它的缺點，不同的初值對于迭代次數，計算速度都有十分重要的影響。

粒子群算法是由Eberhart和Kennedy于1995年提出的一種模仿鳥群尋找食物的隨機搜索算法。從本質上講，粒子群算法是一種群體智能的進化算法，它以粒子的位置(優化問題的解)為運算對象，使各粒子不斷以自身最好位置(個體最好解)和種群最好位置為引導，調整飛行速度和方向，并在迭代飛行中更新個體最好解和全局最好解，最終逼近全局最優解。

與傳統算法相比，簡單遺傳算法更容易求解高維水庫的優化調度問題，但其編碼的設計導致了算法的搜索效率較低。

粒子群算法是由Eberhart和Kennedy于1995年提出的一種模仿鳥群尋找食物的隨機搜索算法。從本質上講，粒子群算法是一種群體智能的進化算法，它以粒子的位置(優化問題的解)為運算對象，使各粒子不斷以自身最好位置(個體最好解)和種群最好位置為引導，調整飛行速度和方向，并在迭代飛行中更新個體最好解和全局最好解，最終逼近全局最優解。

2 建立模型

水火電站的問題關鍵在于最小化火電廠的煤耗成本，同時利用水力資源盡可能的多。目標函數與相關的約束如下：

負荷平衡約束：

梯級水電站的水量:

Vm,t+1=Vm,t+Im,t-Qm,t-Sm,t+Qm,t(t-τi-1)+Sm,t(t-τi-1)

水電轉換關系:

水庫需水量約束:

水電站的發電引用流量約束:

水電機組的出力約束:

火電機組的出來約束

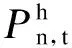
3 粒子群算法

粒子群算法(pso)是在1995年被提出的一種啟發式算法。PSO模擬鳥群的捕食行為。設想這樣一個場景：一群鳥在隨機搜索食物。在這個區域里只有一塊食物。所有的鳥都不知道食物在哪里。但是他們知道當前的位置離食物還有多遠。最簡單有效的方法就是搜尋目前距離食物最近的鳥的周圍區域。PSO從這種模型中得到啟示并用于解決優化問題。PSO中，每個優化問題的解都是搜索空間中的一只鳥。我們稱之為"粒子”。所有的粒子都有一個由被優化的函數決定的適應值，每個粒子還有一個速度決定他們飛翔的方向和距離。然后粒子們就追隨當前的最優粒子在解空間中搜索，具體來說，PSO初始化為一群隨機的粒子(隨機解)，然后通過迭代找到最優解，在每一次迭代中，粒子通過跟蹤兩個“極值”來更新自己。第一個就是粒子本身所找到的最優解，這個解叫做個體極值pBest,另一個極值是整個種群目前找到的最優解，這個極值是全局極值gBest。

4 算例

為了求解出更好的優化結果，取自文獻[6]的測試系統被使用。系統由一個火電站和四個沿河而建的水電站組成，如圖1水力系統測試網絡。調配周期為1天，時間間隔為1個小時。用于本測試網絡的細節數據在表1～3中給出。表1是1天的用戶的負荷需求。表2是各水電站的發電系數。表3是水庫庫容，發電流量的范圍。四個水電站的每小時的來水徑流分別是[10000 8000 1000 0],水流傳輸的延遲時間分別是，目標函數的系數分別是1000,10,0.5。

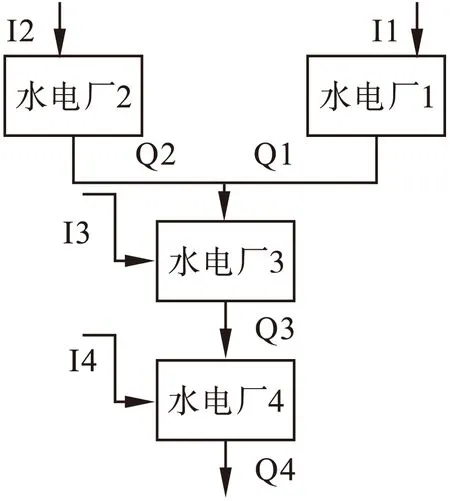
圖1

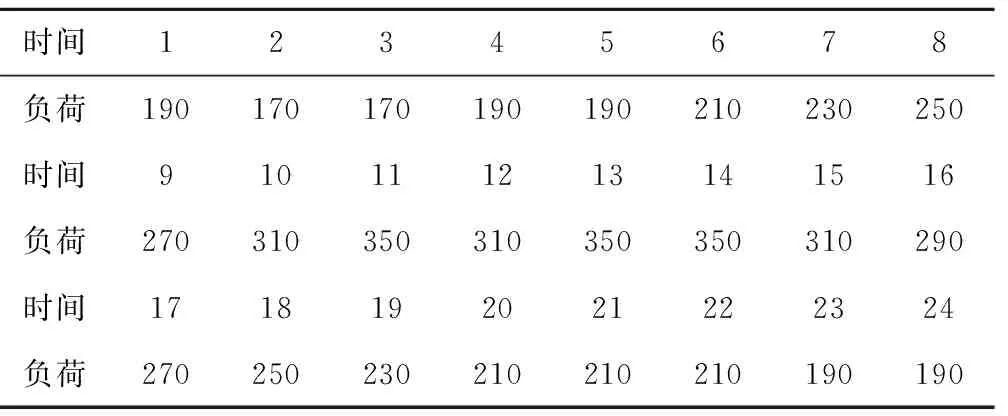
時間12345678負荷190170170190190210230250時間910111213141516負荷270310350310350350310290時間1718192021222324負荷270250230210210210190190

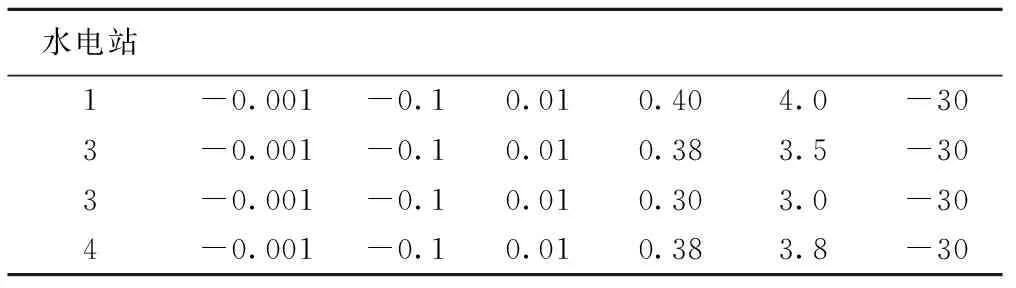
表2

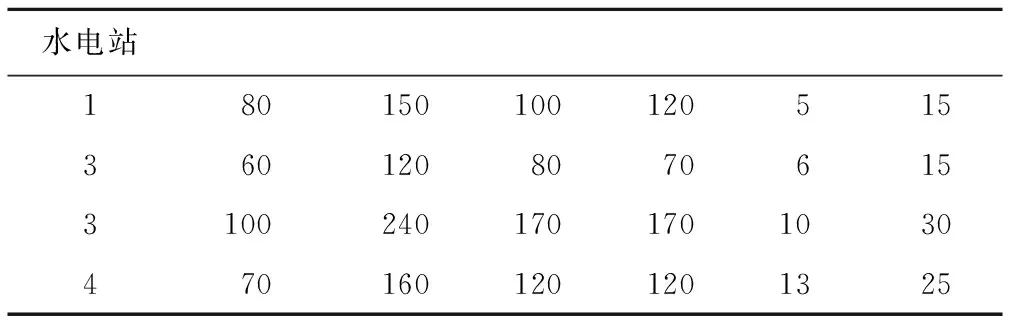
表3

5 結論

表4是用粒子群算法計算的4個水電站和1個火電站的發電量的結果。粒子群算法結果比較好，火電廠的最小秏煤量是154338.1。

表4

[1] 侯貿軍,羅春輝,隗霖捷,等.基于微分進化算法的水火電短期優化調度的研究[J].電力系統保護與控制,2015(9)63-70.

[2] Yang J,Chen N.Short-term hydrothermal coordination using multipass dynamic programming.IEEE Trans Power Syst,1989,4(3):1050-1056.

[3] Tang J,Peter B.Hydrothermal scheduling via extended differential dynamic programming and mixed coordination.IEEE Trans Power Syst,1995,10(4):2021-2028.

[4] Turgeon A.Optimal short-term hydro scheduling from the principle of progressive optimality.Water Resour Res,1981,17(3):481-486.

[5] 張景瑞，龍健，岳超群,等.水火電力系統短期優化調度的一種改進粒子群算法[J].控制與決策,2011(3):89-94.

[6] Naresh R,Sharma J.Two-phase neural network based solution technique for short term hydrothermal scheduling.IEE Proc Gener Transm Distrib,1999,146(6):657-663.