從一道試題探究圓錐曲線的一組優(yōu)美性質(zhì)

北京市第十二中學(xué)高中部 (100071) 劉 剛 趙 毅

從一道試題探究圓錐曲線的一組優(yōu)美性質(zhì)

北京市第十二中學(xué)高中部 (100071)
劉 剛 趙 毅

在2017年1月北京市豐臺(tái)區(qū)高三期末文科數(shù)學(xué)出了這樣一道試題：

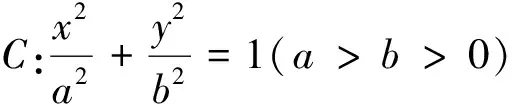
(1)求橢圓C的方程；

(2)過F且斜率為1的直線交橢圓于M，N兩點(diǎn)，P是直線x=4上任意一點(diǎn)．求證：直線PM，PF，PN的斜率成等差數(shù)列．

試題考查了橢圓的標(biāo)準(zhǔn)方程、幾何性質(zhì)、直線與橢圓的位置關(guān)系及坐標(biāo)法的應(yīng)用，經(jīng)過對(duì)(2)問的一般化探究及類比推廣，可以得到圓錐曲線的一組優(yōu)美性質(zhì)．

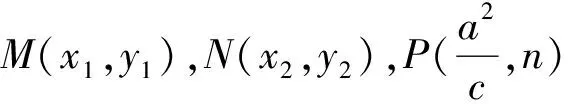
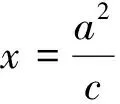
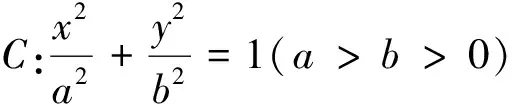
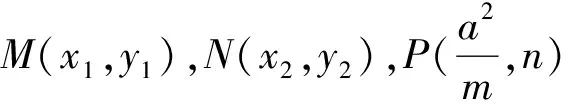
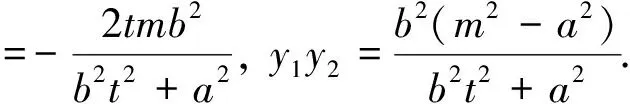
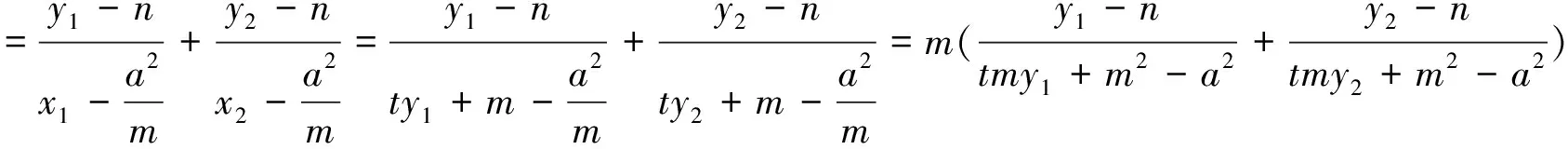
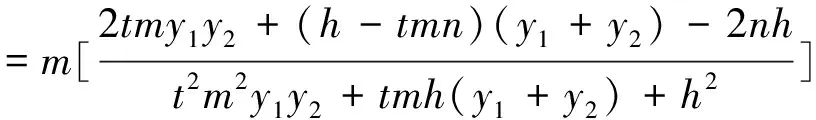
注:當(dāng)m=c時(shí)，性質(zhì)2就變?yōu)榱诵再|(zhì)1，所以性質(zhì)1是性質(zhì)2的特例．另外由橢圓類比到雙曲線、拋物線可得性質(zhì)3與性質(zhì)4.

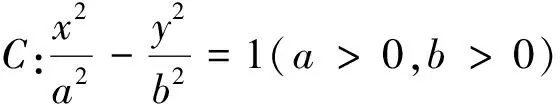
(證明可參考性質(zhì)2的證明過程，限于篇幅，此處省略)

性質(zhì)4 過點(diǎn)Q(m,0)(m≠0)的直線交拋物線C:y2=2px(p>0)于M，N兩點(diǎn)，P是直線x=-m上任意一點(diǎn)，則直線PM，PQ，PN的斜率成等差數(shù)列．

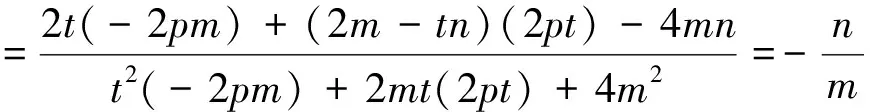
[1]劉剛，趙毅．2016年高考江蘇卷數(shù)學(xué)14題的探究與啟示[J]．中學(xué)數(shù)學(xué)研究(江西)，2016，9．

[2]劉剛，趙毅．一道以圓為背景的高三聯(lián)考試題的探究歷程[J]．中學(xué)數(shù)學(xué)研究(江西)，2016，10．

*本文系北京市豐臺(tái)區(qū)“十三五”重點(diǎn)課題《新課程背景下高中數(shù)學(xué)競賽教學(xué)研究》(課題批準(zhǔn)號(hào)：2016237-J)階段成果之一．