涉及三角形角平分線的兩個對稱不等式

江蘇省海頭高級中學 (222111) 劉永巖

涉及三角形角平分線的兩個對稱不等式

江蘇省海頭高級中學 (222111)
劉永巖

為了書寫上方便，下面我們用記號∑表示循環和，如∑a=a+b+c，∑ab=ab+bc+ca等,文[1]給出如下的一個旁切圓與邊長的不等式：

已知ra,rb,rc是ΔABC的邊a,b,c分別為鄰邊的旁切圓的半徑，則∑(ra-rb)2≥∑(a-b)2.

文[2]給出中線、高與邊長的兩個不等式：

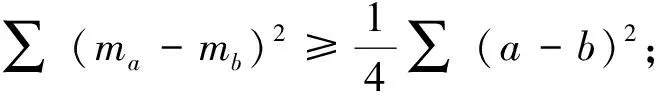
(2)記ΔABC三邊為a,b,c，相應邊上的中線長為ha,hb,hc,則∑(ha-hb)2≥∑(a-b)2.

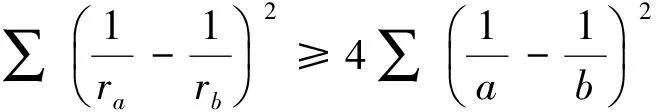
受其啟發，筆者得到如下兩個不等式：

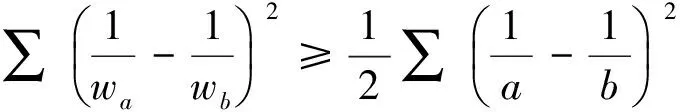
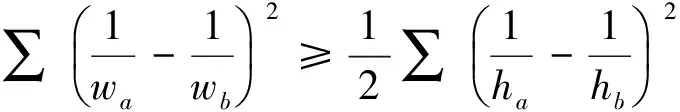
為了證明上述兩個不等式，我們介紹下面一個不等式

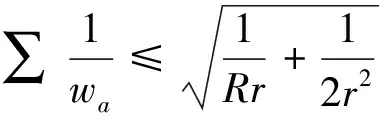
證:根據三角形角平分線公式及柯西不等式，有

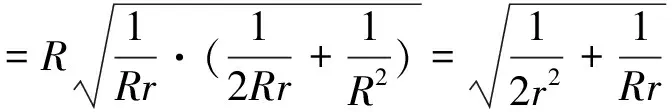
下面我們證明結論1,2:

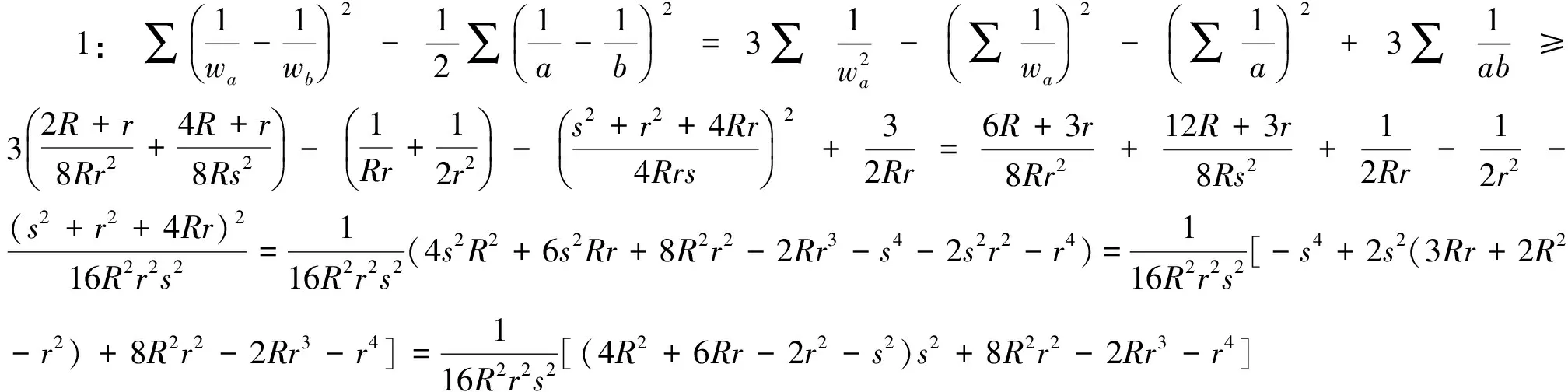
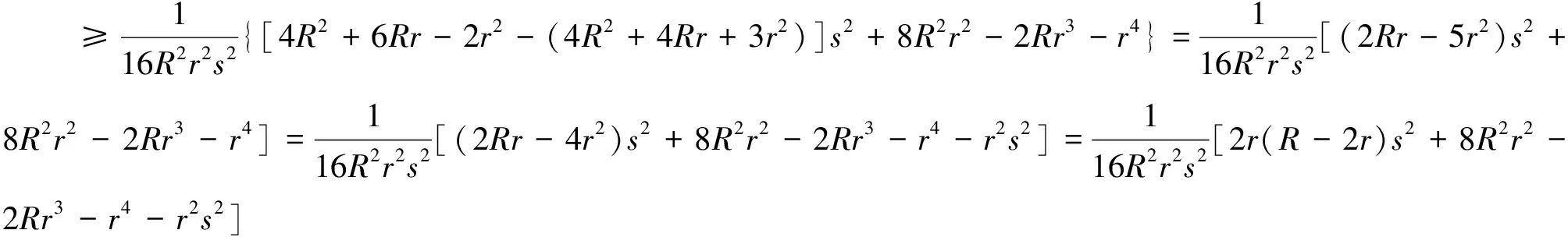
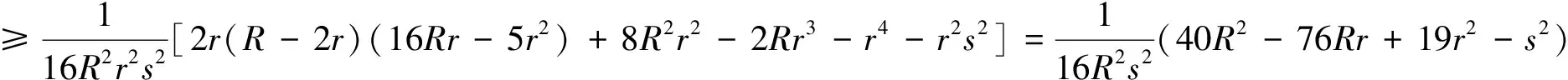
由Gerretsen不等式s2≤4R2+4Rr+3r2,

由Euler不等式R≥2r可知④式≥0，故原不等式成立.

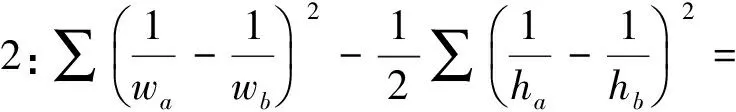
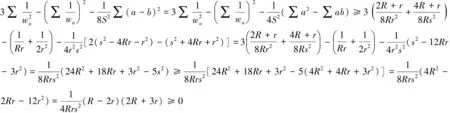
故原不等式成立.

注：此不等式為劉保乾在《110個有趣的不等式問題》[5]中提出的LBQ25(C)問題.

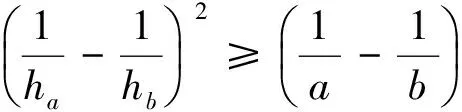
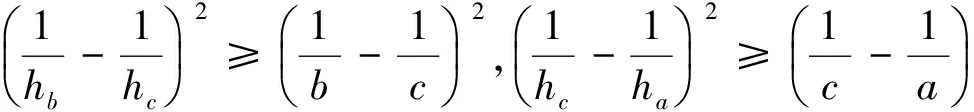
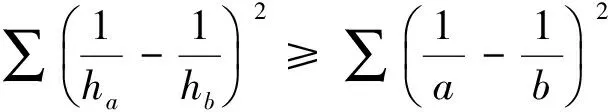
故我們可以得到不等式鏈

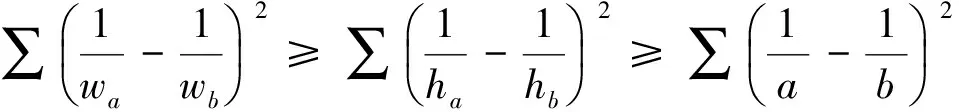
[1]秦慶雄.一個漂亮的幾何不等式[J].數學通訊(下半月).2009.6.

[2]侯典峰.兩個優美的幾何不等式[J].中學數學.2010.6.

[3]董林.對一個優美幾何不等式的研究[J].中學數學.2011.2.

[4]楊學枝.關于角平分線的一個不等式[J].數學通訊.1995.8.

[5]楊學枝.不等式研究[M].拉薩:西藏人民出版社,2003.393-394.