3正則的ID-因子臨界圖

梁彩霞

（肇慶學(xué)院 數(shù)學(xué)與統(tǒng)計學(xué)院，廣東 肇慶 526061）

3正則的ID-因子臨界圖

梁彩霞

（肇慶學(xué)院 數(shù)學(xué)與統(tǒng)計學(xué)院，廣東 肇慶 526061）

如果對于G中任意和 ||V(G)有相同奇偶性的獨立集I,G-I有完美匹配,則稱圖G是ID-因子臨界圖，給出了3-正則的ID-因子臨界圖的刻畫.

完美匹配;3-正則;獨立集;ID-因子臨界圖

1 概述

文中未定義的術(shù)語和概念參見文獻(xiàn)[1].本文涉及的圖為有限、無向的簡單圖.令S為圖G的頂點的子集，G-S的奇分支數(shù)記為o(G-S).設(shè)u是G中任一頂點，記意2點不相鄰,則稱I為獨立集.若G的所有頂點的度都等于k,則稱G為k-正則圖.圖G不包含K1,3為導(dǎo)出子圖，稱之為無爪圖.對邊集M?E(G),如果G的任意頂點至多與M中的1條邊關(guān)聯(lián),則稱M是G的匹配.稱覆蓋所有頂點的匹配為完美匹配.

因子理論一直是圖論中的重要研究領(lǐng)域[2],對因子理論的研究最早可以追溯到1個世紀(jì)以前.1891年，Peterson[3]指出：2-邊連通的3-正則圖有1-因子，這被認(rèn)為是現(xiàn)代因子理論研究的開始.1947年，Tutte[4]給出一個普通圖G有1-因子的充要條件,該結(jié)論是因子理論中最基本的理論,奠定了因子理論的基礎(chǔ).1952年，Tutte[5]又給出圖G有 f-因子的充要條件；1970年，Lovász[6]得到一個圖G有(g,f)-因子的充要條件.從那時起，關(guān)于圖的因子理論的結(jié)果不斷涌現(xiàn).如果對于G中任意頂點u,G-u有完美匹配(即1-因子)，則稱G是因子臨界圖.在文獻(xiàn)[7]中,原晉江把因子臨界圖的概念推廣為獨立集可削去的因子臨界圖.如果對于G中任意和 ||V(G)有相同奇偶性的獨立集I,G-I有完美匹配，則稱圖G是獨立集可消去的因子臨界圖(簡稱為ID-因子臨界圖).ID-因子臨界圖的研究成果可參見文獻(xiàn)[8-12].本文刻畫了3-正則的ID-因子臨界圖，進(jìn)一步完善了圖的因子理論.

2 主要結(jié)果與證明

引理1[4]若圖G有完美匹配,當(dāng)且僅當(dāng)對任意的S?V(G),o(G-S)≤ ||S.

由圖的正則性，在以下的討論中G中頂點的個數(shù)為偶數(shù).

定理1 無爪的3-正則ID-因子臨界圖只有圖1中的G1,G2及G3.

證 易驗證G1,G2及G3都是無爪的3-正則ID-因子臨界圖.設(shè)G是無爪的3-正則ID-因子臨界圖，下面證明G同構(gòu)于G1,G2或G3.設(shè)u是G中任一頂點，由G是無爪圖知1≤f(u)≤3.

情形1 f(u)=1.

在該情形下，2≤ ||N(2)(u)≤4.不失一般性，不妨設(shè)x1與x2相鄰，由G的正則性知x3與N(2)(u)中的2個頂點，不妨設(shè)為y1與y2相鄰，且由G無爪知y1與y2相鄰.

當(dāng) ||N(2)(u)=2時，由G是3-正則的知xi(i=1,2)與且僅與y1和y2中之一相鄰，yi(i=1,2)與且僅與x1和x2中之一相鄰，此時G?G1.

當(dāng) ||N(2)(u)=3時，不失一般性，設(shè)另有y3∈N(2)(u),且y3與x1相鄰.若x2也與y3相鄰，取I={ } x3,y3，則G-I含有奇分支，與引理1矛盾，從而x2與y3不相鄰.不妨設(shè)x2與y2相鄰，則有y1與y3必不相鄰，否則圖G含有以y3為中心的爪.從而I={ } y1,y3是G中的獨立集,且G-I含有奇分支，矛盾.

當(dāng) ||N(2)(u)=4時,不失一般性，設(shè)另有y3,y4∈N(2)(u),且y3與x1相鄰，y4與x2相鄰.斷言1 y3與y1和y2不相鄰，y4與y1和y2不相鄰.

若y3與y1相鄰，則y3與y2也相鄰，否則含爪.由G是3-正則的，有取含有奇分支,矛盾，從而有y3與y1不相鄰，類似地有y3與y2不相鄰，y4與y1,y2不相鄰.

斷言2 y3與y4不相鄰.

假設(shè)y3與y4相鄰，且y3與z∈N(3)(u)相鄰.若y4與z相鄰，取I={ } z,x3,G-I含有奇分支,矛盾；若y4與z不相鄰，取

否則，設(shè)w∈N(4)(u),由斷言2知是圖G中的獨立集，但G-I含有奇分支,矛盾.

當(dāng) |N(3)(u)|=6時，由G的正則性知與且僅與N(2)(u)中的1個頂點相鄰.不妨設(shè)y1與z1相鄰，取獨立集則G-I含有奇分支,矛盾．

情形2 f(u)=2.

不失一般性，設(shè)x1,x2均與x3相鄰.在這種情形下

情形3 f(u)=3.

顯然，此時G?K4=G3.

定理2 含爪的3-正則ID-因子臨界圖只有圖2中的G4,G5,G6,G7,G8.

證 易驗證圖2中的Gi(i=4,5,6,7,8)是含爪的3-正則ID-因子臨界圖.設(shè)G是含爪3-正則ID-因子臨界圖，下證明G同構(gòu)于圖2中的Gi(i=4,5,6,7或8).不妨設(shè)G′是G中的1個爪,其中V(G′)={ } u,x1,x2,x3,u是該爪的中心.

由定理1和定理2顯然有以下推論1.

推論1 3-正則的ID-因子臨界圖有且只有8個，見圖1和圖2.

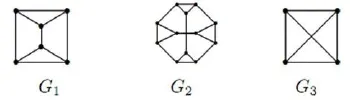
圖1 無爪的3-正則ID-因子臨界圖

[1] BONDY JA,MURTY S R.Graph theory with applications[M].London:Macmillan Press Ltd,1976.

[2] 于青林,劉桂真.圖的因子和匹配可擴(kuò)性[M].北京：高等教育出版社,2010.

[3] PETERSEN J.Die theorie der regul?ren[J].AetaMath,1891,15:193-220.

[4] TUTTE W T.The factorizations of linear graphs[J].London Math Soc,1947,22:107-111.

[5] TUTTE W T.The factors of graphs[J].Can J Math,1952(4):314-328.

[6] LOVáSZ.Subgraphs with prescribed valancies[J].J Comb Theory Ser B,1970(9):391-416.

[7] YUAN Jinjiang.Independent-set-deletable factor-critical power graphs[J].Acta Mathematica Scientia,2006,26B(4):577-584.

[8] LIU Yan.The degree conditions of ID-factor-critical graphs[J].SouthestAsian Bulletin of Mathematics,2003,27:641-648.

[9] LIANG Caixia,LIU Yan.The degree sum conditions of ID-factor-critical Graphs[J].Chinese Journal of Engineering Mathematics,2006,23:169-174.

[10] 馬芳,劉巖.獨立集可削去的因子臨界圖和無爪的獨立集可削去因子臨界圖的度條件[J].華南師范大學(xué)學(xué)報(自然科學(xué)版),2008(2):29-33.

[11] MA Fang,LIU Yan.ID-factor-critical and claw-free graphs of diameter 2[J].Southeast Asian Bulletin of Math，2009,33:879-883.

[12] LIANG Caixia,LIU Yan.ID-factor-critical claw-free Graphs[J].Pacific Journal ofApplied Mathematics,2013,4(5):253-258.

3-Regular ID-Factor-Critical Graphs

LIANG Caixia

(School of Mathematics and Statistics,Zhaoqing University,Zhaoqing,Guangdong 526061,China)

:Gis ID-factor-critical if for every independent setIofGwhich has the same parity with ||V(G), G-Ihas a perfect matching.The 3-regular ID-factor-critical Graphs are characterized.

:perfect matching;3-regular;independent set;ID-factor-critical

O157.5

A

1009-8445（2017）02-0008-04

（責(zé)任編輯：陳 靜）

2016-07-01

廣東省自然科學(xué)基金資助項目（2014A030310277）；肇慶學(xué)院教學(xué)質(zhì)量工程項目（80111323）

梁彩霞（1978-），女，廣東茂名人，肇慶學(xué)院數(shù)學(xué)與統(tǒng)計學(xué)院講師，碩士.