有翼導彈動態氣動特性數值研究

張瑞民,時曉天

(中國航天空氣動力技術研究院,北京 100074)

有翼導彈動態氣動特性數值研究

張瑞民,時曉天

(中國航天空氣動力技術研究院,北京 100074)

為準確預測飛行器的機動特性,故開展其動態氣動特性研究。應用非結構動網格技術建立了可模擬飛行器作周期性俯仰運動的強迫振蕩法。選取NACA 0012翼型為研究對象對該方法進行驗證,進而計算了有翼導彈Finner在各馬赫數下的靜、動導數,并分析了Finner導彈在不同減縮頻率下的動態氣動遲滯特性。結果表明,文中方法能夠有效模擬有翼導彈在不同馬赫數下的動態氣動特性,結果正確可靠,具有較高的工程應用價值。

有翼導彈;動態特性;氣動特性;動網格;俯仰振蕩

0 引言

對于新一代高性能戰斗機和導彈而言,必須要具備大攻角機動的飛行能力。因此,準確的預測飛行器的動態性能顯得尤為重要。

1990年之前,動導數預測以風洞實驗和工程估算為主。然而,工程估算僅適用于簡單外形,且無法滿足不同工況下的動導數預測;風洞實驗對模擬技術、測量手段要求較高,且實驗費用昂貴,更不可避免地存在著系統機構阻尼、支架干擾、洞壁干擾及重心位置干擾等因素,大大影響了實驗結果的準確性。數值模擬方法不存在上述問題,但也面臨著一系列的重大挑戰,尤其是非定常模擬的效率問題和精度問題[1]。

隨著計算機性能的提高以及非定常流場數值模擬技術的飛速發展,應用數值方法來預測飛行器的動態氣動特性日益成熟。文獻[2-7]采用當地活塞理論方法或者改進的工程計算方法研究了飛行器作周期性振蕩的動態氣動特性;文獻[8]采用諧波平衡法預測了飛行器的周期性非定常流動特性,計算效率很高;文獻[9-17]采用數值模擬技術研究了各種飛行器作俯仰振蕩運動的動態特性;文獻[18-19]采用CFD技術計算了飛行器的動導數,還分析了減縮頻率對動態特性的影響。

借鑒前人的研究成果,文中應用非結構化動網格技術模擬了Finner導彈繞固定軸旋轉作俯仰振蕩運動的整個過程,計算了該導彈在不同馬赫數下的靜、動導數,并對該導彈在不同減縮頻率的動態氣動特性進行了分析。

1 數值方法

1.1 數值算法與湍流模型

文中采用Transition SST湍流模型進行計算,該模型是在SSTk-w的基礎上增加了有關間歇度γ和轉捩發生準則的兩種輸運方程,其捕捉流場細節精度更高。

1.2 控制方程與離散方法

流場計算采用Pressure-Velocity Coupling算法中的Coupled方法來求解三維非定常可壓粘流時均N-S方程。空間離散采用格心格式的有限體積法,時間離散采用隱式離散方法進行雙時間推進。

1.3 動網格技術

動網格技術可以用來模擬流場邊界隨時間變化的問題。網格的更新過程是根據每次迭代中邊界的變化情況自動完成。在任一控制單元中,廣義標量Φ的積分守恒方程為:

(1)

式中:ρ為流體密度;u為速度流量;ug為移動網格的網格速度;Γ為擴散系數;SΦ為源項;?V為控制單元V的邊界;A為控制單元的面積。

1.4 網格劃分與邊界條件

文中采用商用軟件ICEM對Finner導彈模型進行了非結構化網格劃分,遠場邊界到翼型表面的距離設為弦長的20倍,翼型表面設定為無滑移壁面邊界,且對翼型附近網格進行了局部加密。

1.5 動導數辨識

對于單自由度強迫俯仰振蕩,其運動形式如下:

α=α0+αmsin(ωt)

(2)

式中:α0為初始攻角;αm為振蕩幅值;ω為振蕩圓頻率。

假設飛行器為對稱直線飛行,且振幅很小,在計算中僅考慮一階動導數,忽略高階動導數,那么,俯仰力矩在初始攻角處作泰勒展開有:

(3)

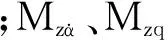
飛行器作低頻小幅振蕩的運動方程簡化如下:

(4)

將式(4)代入式(3),合并同類項,可得:

(5)

式(5)沿遲滯環線積分,可得:

(6)

由此可得:

(7)

通過無因次化,可得:

(8)

式中：k=ωlref/2V為減縮頻率;lref為模型參考長度;v為來流速度。

2 方法驗證

采用國際標準算例AGARD CT5[20]來驗證文中方法。NACA 0012翼型作俯仰振蕩運動,其軸心位于翼型前緣1/4弦長處,計算狀態如表1。

表1 計算條件

圖1和圖2分別給出了升力系數和俯仰力矩系數隨迎角變化的遲滯曲線。從圖中可以看出,文中結果與實驗數據及參考值吻合較好,表明文中數值方法正確可靠。

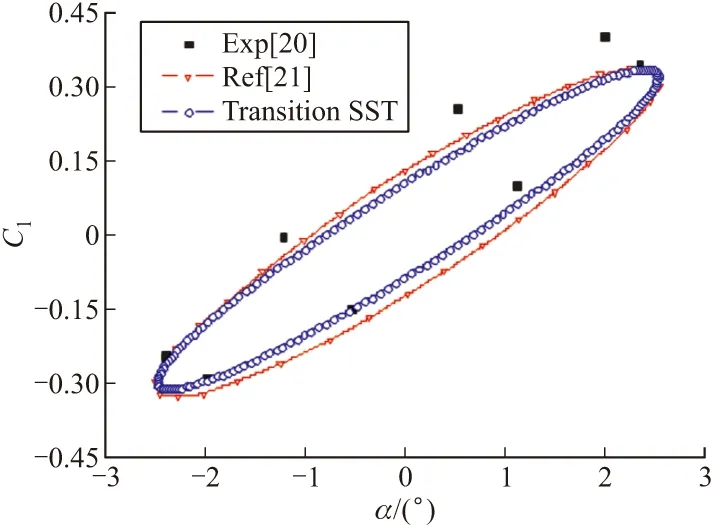
圖1 升力系數隨迎角的變化

圖2 俯仰力矩系數隨迎角的變化

3 算例與分析

3.1 模型與網格

算例選取國際動導數標模Finner導彈[22],幾何外形見圖3,模型網格劃分見圖4。

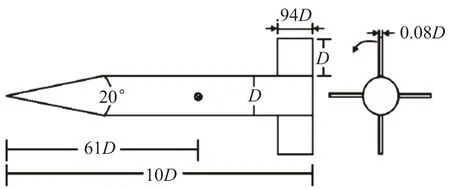
圖3 導彈外形示意圖

圖4 Finner模型網格

3.2 靜導數計算

圖5和圖6分別給出了0°攻角、0.5～4.5Ma下的Finner導彈的法向力和俯仰力矩靜導數系數,并與文獻[22-23]中的實驗數據和計算結果進行了比較。從圖中可以看出,與參考值相比,文中結果更接近于實驗結果。圖7給出了Finner導彈在0°攻角下、Ma=0.9時x-z對稱面的馬赫數云圖。從圖中可以清楚地看到彈體頭部和尾翼后側的激波形成以及彈體尾端的低速流動區域。

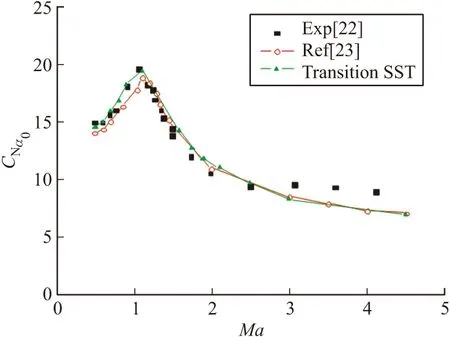
圖5 Finner導彈在0°攻角時、不同馬赫數下的法向力靜導數

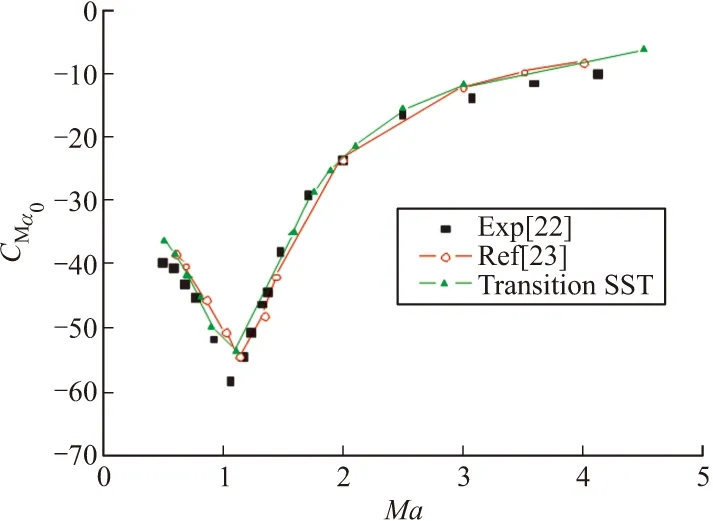
圖6 Finner導彈在0°攻角時、不同馬赫數下的俯仰力矩靜導數

圖7 Finner導彈在0°攻角時、0.9Ma x-z對稱面的馬赫數云圖

3.3 動導數計算

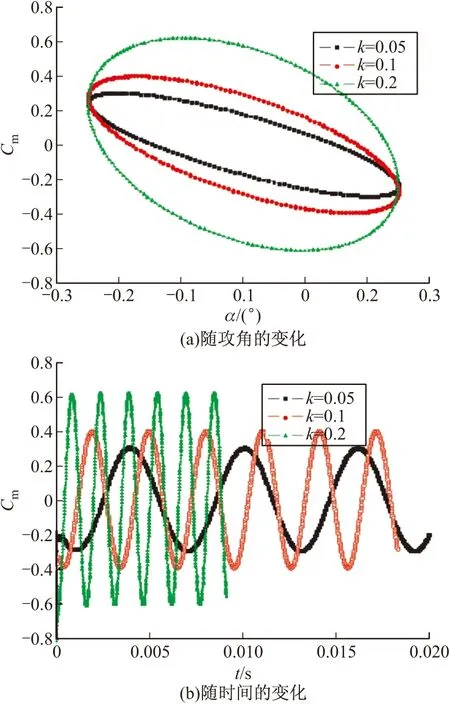
Finner導彈動導數的計算條件見表2。圖8給出了0°攻角、0.5～4.5Ma下Finner導彈的俯仰力矩動導數,并與文獻[21-22]中的實驗數據和計算結果進行了比較。可以看出,除0.9

表2 計算條件

圖8 Finner導彈在0°攻角、不同馬赫數的俯仰組合動導數

3.4 減縮頻率影響

圖9給出了馬赫數為0.9時不同減縮頻率下Finner導彈的俯仰力矩系數隨著攻角和時間的變化。可以看出,俯仰力矩系數隨攻角變化的遲滯曲線圖均以(α,Cm)=(0,0)為圓心,且隨著減縮頻率的增加,離心率不斷減小;俯仰力矩系數隨著時間變化的曲線圖呈正弦波,且隨著減縮頻率的增加,正弦波的頻率和幅值均增大。圖10給出不同馬赫數下俯仰阻尼動導數系數隨減縮頻率的變化。從圖中可以看出,當減縮頻率在0.025到0.1之間時,隨著減縮頻率的增加,俯仰阻尼動導數系數變化較大;當減縮頻率大于0.1時,俯仰阻尼動導數系數基本不變。

圖9 0.9 Ma下不同減縮頻率對俯仰力矩系數的影響

圖10 不同馬赫數下減縮頻率對俯仰阻尼動導數系數的影響

4 結論

文中應用計算流體力學軟件Fluent中的動網格技術和UDF方法模擬了Finner導彈作俯仰振蕩運動的動態氣動特性,并與參考文獻中的實驗數據和計算結果進行了比較,得出的主要結論如下:

1)文中關于Finner導彈在亞跨超高速不同馬赫數下靜、動導數的預測結果很好,說明文中數值方法正確可靠。

2)俯仰力矩系數隨著攻角變化的遲滯曲線圖以(α,Cm)=(0,0)為圓心,且隨著減縮頻率的增加,離心率不斷減小;俯仰力矩系數隨著時間變化的曲線圖呈正弦波,且隨著減縮頻率的增加,正弦波的頻率和幅值均增大。

3)當減縮頻率在0.025～0.1之間,隨著減縮頻率的增加,俯仰阻尼動導數系數變化較大;當減縮頻率大于0.1時,俯仰阻尼動導數系數基本不變。

[1] 李周復. 風洞特種實驗技術 [M]. 北京: 航空工業出版社, 2010: 240-242.

[2] TONG B G, HUI W H. Unsteady embedded Newton-Busemann flow theory [J]. Journal of Spacecraft and Rockets, 1986, 23(2): 129-135.

[3] EAST R A, HUTT G R. Comparison of predictions and experimental data for hypersonic pitching motion stability [J]. Journal of Spacecraft and Rockets, 1988, 25(3): 225-233.

[4] 張偉偉, 史愛明, 王剛, 等. 結合定常CFD技術的當地流活塞理論 [J]. 西北工業大學學報, 2004, 22(5): 545-549.

[5] ZHANG Weiwei, YE Zhengyin, ZHANG Chenan, et al. Supersonic flutter analysis based on local piston theory [J]. AIAA Journal, 2009, 47(10): 2321-2328.

[6] 盧學成, 葉正寅, 張偉偉. 超音速、高超音速飛行器動導數的高效計算方法 [J]. 航空計算技術, 2008, 38(3): 28-31.

[7] 劉溢浪, 張偉偉, 田八林, 等. 一種超音速高超音速動導數的高效計算方法 [J]. 西北工業大學學報, 2013, 31(5): 824-828.

[8] 陳琦, 陳堅強, 袁先旭, 等. 諧波平衡閥在動導數快速預測中的應用研究 [J]. 力學學報, 2014, 46(2): 183-190.

[9] DUBUC L, CANTARITI F, WOODGATE M, et al. Solution of the unsteady Euler equations using an implicit dual-time method [J]. AIAA Journal, 1998, 36(8): 1417-1424.

[10] PARK S H, KIM Y, KWON J H. Prediction of dynamic damping coefficients using unsteady dual-time stepping method: AIAA 2002-0715 [R]. 2002: 1-9.

[11] OKTAY E, AKAY H U. CFD predictions of dynamic derivatives for missiles: AIAA 2002-0276 [R]. 2002: 1-10.

[12] GREEN L L, SPENCE A M, MURPHY P C. Computational methods for dynamic stability and control derivatives: AIAA 2004-0015 [R]. 2004: 1-17.

[13] MURMAN S M. Reduced-frequency approach for calculating dynamic derivatives [J]. 2007, 45(6): 1161-1168.

[14] 袁先旭, 張涵信, 謝昱飛. 基于CFD方法的俯仰靜、動導數數值計算 [J]. 空氣動力學學報, 2005, 23(4): 458-463.

[15] 史愛明, 楊永年, 葉正寅. 結合CFD技術的跨音速動導數計算方法研究 [J]. 西北工業大學學報, 2008, 26(1): 11-14.

[16] 范晶晶, 閻超, 李躍軍. 飛行器大迎角下俯仰靜、動導數的數值計算 [J]. 航空學報, 2009, 30(10): 1846-1850.

[17] 孫智偉, 程澤蔭, 白俊強, 等. 基于準定常的飛行器動導數的高效計算方法 [J]. 飛行力學, 2010, 28(2): 28-30.

[18] 孫濤, 高正紅, 黃江濤. 基于CFD的動導數計算與減縮頻率影響分析 [J]. 飛行力學, 2011, 29(4): 15-18.

[19] BATINA J T. Unsteady Euler airfoil solutions using unstructured dynamic meshes [J]. AIAA Journal, 1990, 28(8): 1381-1388.

[20] LANDON R H. NACA 0012 oscillatory and transient pitching: ADP 010 707 [R]. 2000.

[21] LI J, HUANG S Z, JIANG S J, et al. Unsteady viscous flow simulations by a fully implicit method with deforming grid: AIAA 2005-1221 [R]. 2005: 1-10.

[22] WEST K O. Comparison of free-flight spark range and wind tunnel test data for a generic missile configuration at mach numbers from 0.6 to 2.5: AFATL-TR-81-87 [R]. Florida:Air Force Armament Laboratory, 1981.

[23] SAHU J. Numerical computations of dynamic derivatives of a finned projectile using a time-accurate CFD method: AIAA 2007-6581 [R]. 2007: 1-13.

Research on Numerical Virtual Flight of Spinning Projectile

ZHANG Ruimin,SHI Xiaotian

(China Academy of Aerospace Aerodynamics, Beijing 100074, China)

In order to accurately predict the maneuvering characteristics of the aircraft, dynamic aerodynamics was then studied. Dynamic unstructured mesh technology in computational fluid dynamics was used to build forced oscillation method which could simulate the periodic pitching motion of the aircraft. The NACA 0012 airfoil was selected as the research object to validate the method. The static and dynamic derivatives winged missile Finner under different Mach numbers were computed and the dynamic aerodynamic hysteresis characteristics under different reduced frequencies were analyzed. The results showed that the method in the paper could effectively and correctly simulate the dynamic aerodynamic characteristics of winged missile under different Mach numbers and it could find wide application in engineering.

winged missile; dynamic characteristics; aerodynamic characteristics; dynamic mesh; pitching oscillation

2016-03-03

張瑞民(1980-),男,山西運城人,高級工程師,博士,研究方向:空氣動力學、飛行動力學和多相流研究。

V211.3

A