基于目標雙參數的末敏彈掃描角自適應調整

韓廣超,王 鋒,趙河明,彭志凌,劉建勛

(中北大學機電工程學院,太原 030051)

基于目標雙參數的末敏彈掃描角自適應調整

韓廣超,王 鋒,趙河明,彭志凌,劉建勛

(中北大學機電工程學院,太原 030051)

針對末敏彈穩態掃描參數恒定,掃描規律一定,對不同參數目標,可能導致漏掃甚至無法及時發現目標的問題,提出了一種基于目標速度與長度的掃描角自適應調整方法。建立了末敏子彈掃描目標的關系模型,通過MATLAB進行了初始掃描角以及穩態掃描掃描角的確定。仿真結果表明:文中提出的掃描自適應調整方法,能快速調整掃描角,提高了掃描效率,便于及時發現目標,對末敏彈設計提供了一定的理論支持和數據參考。

末敏彈;掃描角;自適應調整;MATLAB

0 引言

末敏彈具有大面積封鎖與殺傷性、效費比高以及打了不用管等優點[1],在現代戰爭中,針對裝甲集群目標精確打擊發揮了極其重要的作用。

從彈道運動角度來看,穩態掃描參數對子彈藥系統性能與可靠性高低起著決定性作用,文獻[2]研究了末敏彈穩態掃描的物理規律;文獻[3-4]對末敏彈掃描角進行了研究;文獻[5-6]對末敏彈穩態掃描特性進行了詳細介紹,但是以上研究均屬于傳統穩態掃描方式,這種方式缺點就是掃描效率低,如果目標處于掃描中心,需長時間才能探測到目標甚至可能因子彈滯空時間長而被擊落。從目標運動角度來看,影響末敏彈掃描效率主要是目標的速度和長度兩種因素,文獻[7-8]針對速度和長度兩種因素就末敏彈的掃描運動只進行了簡單敘述與介紹,沒有深入研究。

未來裝甲坦克為提高機動性,實現快速部署以及提高戰場生存力,將會向高速、小型化方向發展[9-10],因此提高末敏彈的掃描效率,改善作戰效能,是研究新一代末敏彈的主要任務之一,根據導彈導引頭掃描技術原理[11-14],提出了基于目標速度與長度雙參數的末敏彈掃描角自適應調整方法。

1 末敏子彈穩態掃描工作原理

末敏彈經火炮發射后,飛行到指定區域上空,母彈開艙拋射子彈體,減速減旋穩定后進入穩態掃描階段,子彈體穩態掃描工作原理如圖1所示。

穩態掃描過程:子彈軸與鉛垂方向成某一角度值θ的子彈在摩擦盤導旋作用下,主旋轉傘帶動子彈同步旋轉,與此同時,位于子彈上的敏感視場在地面以螺旋線的形式由外向內開始對目標進行搜索、探測、識別,一旦識別目標,即刻形成爆炸成型彈丸(explosively formed projectile,EFP),從頂部攻擊裝甲集群目標。

圖1 末敏子彈穩態掃描原理圖

假設子彈穩態掃描的初始高度為H,在螺線上的初始掃描位置為A0,初始位置與X軸成α,經時間t后為掃描螺線上的A1點,其坐標表示為:

(1)

由式(1)可得出掃描軌跡的極坐標:

r(t)=(H-vt)tanθexp(i(α+wt))

(2)

根據式(2)可知兩相鄰掃描螺線的距離為:

Δ=vtanθ/n

(3)

n=w/2π是子彈繞鉛垂軸的角速度(r/s)。

2 末敏子彈掃描角自適應調整

2.1 末敏子彈掃描目標關系模型的分析與建立

根據文獻[15]中研究識別方式對捕獲準則的影響可知:在擺幅不大的情況下,“一次掃描”方式命中概率較高,因此,假設捕獲準則為一次掃描,同時假設子彈在進行穩態掃描時目標處于掃描區域內部靠近中心處,目標如果要被掃描軌跡所覆蓋,必須滿足子彈在一個掃描周期內,目標向前行駛的距離為坦克標準長度減去N個掃描螺距,其中N≥1,目標運動與掃描軌跡關系如圖2、圖3、圖4所示。

圖2 目標未接觸掃描軌跡線

因此用末敏彈攻擊目標的理論速度值為:

(4)

式中N≥1且為整數值,L為坦克的標準長度。

圖3 目標開始接觸掃描軌跡線

圖4 目標穿過掃描軌跡線

戰場上,如果目標速度與根據式(4)計算的理論值滿足前者小于等于后者的話,可以用末敏彈進行攻擊[16],但未來坦克如果滿足前者大于后者的話,傳統末敏彈將失去作用,為解決這方面的問題根據式(3)和式(4)從穩態掃描參數考慮,轉速和落速均與主旋轉傘有關,主旋轉傘一旦設計好,轉速和落速也就確定了[17],因此應從掃描角考慮,滿足的關系式如下:

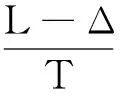
(5)

式(5)為子彈體掃描目標運動模型,如果目標標準長度減小,則理論速度減小,在目標速度增大的同時,若增大理論速度值,可減小掃描角,直到計算的理論速度值大于等于目標的速度為止。

2.2 末敏子彈掃描角自適應調整原理分析

根據式(5),如果目標速度大于理論速度時,通過降低掃描角來增大理論速度,所以掃描角自適應調整原理為:每完成一次掃描周期,掃描角θ變化一個Δθ,使得相鄰兩個掃描周期探測區域相切,可以避免探測區域重合,提高掃描效率。其自適應調整原理如圖5所示。

圖5 掃描角自適應調整原理

Hn為當前時刻子彈距地面的高度,Hn+1為下一時刻子彈距地面的高度,兩者之間時間差為一個掃描周期,A點為兩次掃描探測區域相切點,則有:

Hntan(θn-δ)=Hn+1tan(θn+1+δ)

(6)

(7)

式中δ為紅外敏感器的視場角,圖6為掃描角自適應調整掃描原理圖。

圖6 末敏子彈掃描角自適應調整原理

2.3 掃描角自適應調整在工程中的實際應用

在2.2節描述的掃描角自適應調整原理中:兩掃描區域相切,避免探測區域重合,在工程實際應用中,為保證目標不被探測器所漏掃,要求探測區域出現一定的重合,因此在實際應用中,需引入掃描角補償系數ε,其作用就是對掃描角進行修正,從而保證探測區域達到一定重合度,同時在設計靜態懸掛角時,掃描角必須設置最低門限值γ和最高門限值β,這樣才能保證有一定的掃描區域,并且保證子彈體系統的穩定性。修正后的掃描角如下:

(8)

根據式(7)和式(8)得出的掃描角就可滿足工程中實際應用。

3 掃描角自適應調整仿真分析

初始參數設定:子彈藥穩態掃描時距地面高度H=600 m,轉速n=4 r/s,落速v=14 m/s,紅外敏感器視場角δ=1.6°目標標準長度L=6 m,目標實際速度定為82.8 km/h,根據式(4)、式(5)、式(7)三式,初步選定初始掃描角即靜懸掛角的范圍為5°～39°。

3.1 初始掃描角和穩態掃描角的確定

根據末敏子彈掃描角自適應調整原理,編寫仿真代碼,仿真得出各初始掃描角下,經自適應調整后達到的穩態掃描角以及所用的時間如表1所示。

表1 初始掃描角與穩態掃描角及時間關系

從表中數據可以看出:

1)時間均為掃描周期的整數倍;

2)掃描角每3°變化,其時間是相同的,最終達到穩態掃描角的范圍基本在1°～4°之間且變化平穩,只有在初始掃描角為29°～32°時,每4°變化。

掃描角選取原則:既保證時間短,又保證掃描角最大,綜合表中數據,將初始掃描角定在7°,確定的穩態掃描角為3.831 7°,此時時間最短為一個掃描周期,穩態掃描角較大,滿足掃描角選取原則。

3.2 掃描軌跡分析

在同一穩態掃描開始高度,同一落速,同一轉速下,傳統末敏彈(掃描角為30°)的掃描軌跡和掃描角自適應調整后的掃描軌跡分別如圖7和圖8所示。

圖7 傳統掃描角為30°時的掃描軌跡

圖8 掃描角自適應調整后的軌跡

傳統掃描角為30°時,目標實際速度要遠大于所計算的理論值,此時不能用末敏彈攻擊目標。為滿足目標實際速度小于等于理論速度,經掃描角自適應調整后,掃描角變得很小,在穩態掃描開始高度相同的情況下,探測器掃描范圍會明顯降低,同時掃描間隔也會大幅減小,這樣會使得目標被掃描到的幾率增加,提高子母彈的作戰效能。

4 結論

文中針對目標長度與速度兩參數,在目標速度大于理論目標速度時,傳統子母彈掃描效率下降,提出了基于目標雙參數的末敏彈穩態掃描角自適應調整方法。通過仿真分析:該方法能夠快速調整掃描角,不僅提高掃描效率,而且能夠及時發現目標。通過分析得出以下幾點結論:

1)根據子彈與目標運動模型可知:掃描角自適應調整中,掃描角逐漸減小,所以從掃描軌跡看方向由外向內,在目標速度較大,標準長度減小的情況下,目標應位于子母彈的掃描軌跡內,因此,在火炮發射末敏彈時,應調整射擊諸元,使目標處于掃描軌跡內。

2)文中提出的掃描角自適應調整方法,對末敏彈的研究與設計提供了一定的技術和方法支持,具有一定的現實指導意義。

3)文中得出的結果存在一種缺陷:當目標的速度和長度確定時,經調整后的穩態掃描角很小,雖然掃描間隔減小了,增加了目標被掃描幾率,但探測器的掃描范圍卻大大的降低了。

4)文中是在理想狀態即無風影響下,對末敏彈掃描角進行的自適應調整研究,但在實際情況下,風的影響可能會對掃描角產生一定的影響,因此研究風作用下的末敏彈掃描角自適應調整對末敏彈的研究與設計更具有一定的現實與應用指導意義。

[1] 鄭榮躍, 秦子增. 子母彈研究進展 [J]. 國防科技大學學報, 1996, 18(1): 60-64.

[2] 李臣明, 韓子鵬, 劉怡昕, 等. 基于四元數法變換的末敏彈掃描運動研究 [J]. 兵工學報, 2009, 30(4): 389-393.

[3] 馬凱臣, 曹詠弘, 范錦彪. 基于公式近似的末敏彈掃描角計算方法 [J]. 探測與控制學報, 2011, 33(5): 52-55.

[4] 劉文舉, 魏琳, 鐘錄宏. 末敏子彈穩態掃描角仿真模型研究 [J]. 彈箭與制導學報, 2010, 30(6): 108-109.

[5] 顧建平, 韓子鵬. 末敏彈掃描運動的影響因素分析 [J]. 彈箭與制導學報, 2009, 29(3): 136-138.

[6] 史金光, 韓子鵬, 舒敬榮, 等. 雙翼型無傘末敏彈穩態掃描運動數學模型 [J]. 彈道學報, 2010, 22(2): 24-27.

[7] 趙新生, 邢立新, 孫超. 末敏彈穩態掃描段掃描間隔分析 [J]. 彈箭與制導學報, 2005, 25(4): 900-902.

[8] 程杰, 張凌海. 末敏彈穩態掃描段掃描間隔對射擊效果的影響分析 [J]. 電腦知識與技術, 2014, 10(20): 4857-4859.

[9] 袁常卿, 蘇鐵熊. 未來坦克裝甲車輛技術的發展趨勢 [J]. 機械管理開發, 2007(1): 11-12.

[10] 郭正祥. 用對比分析法評判坦克優劣——世界坦克排行榜值得商榷 [J]. 國外坦克, 2012(10): 13-17.

[11] 吳文超, 黃長強, 王志軍, 等. 某型導彈導引頭定向掃描技術 [J]. 空軍工程大學學報(自然科學版), 2010, 11(3): 30-34.

[12] CARLSON B D, EVANS E D, WILSON S L. Search radar detection and track with the hough transform: Part Ⅰ System concept [J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 102-108.

[13] CARLSON B D, EVANS E D, WILSON S L. Search radar detection and track with the hough transform: Part Ⅱ Detection statistics [J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 109-115.

[14] CARLSON B D, EVANS E D, WILSON S L. Search radar detection and track with the hough transform: Part Ⅲ Detection performance with binary integration [J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 116-125.

[15] 楊紹卿. 末敏彈系統理論 [M]. 西安: 陜西科學技術出版社, 2009: 54-67.

[16] 翟保磊, 李波, 高曉光. 基于掃描角控制的末敏彈穩態掃描方法 [J]. 電光與控制, 2013, 20(6): 58-61.

[17] 楊紹卿. 靈巧彈藥工程 [M]. 北京: 國防工業出版社, 2010: 149-157.

Self-adaptive Adjustment of the Scanning Angle of Terminal-sensitivity Projectile Based on Target Double Parameters

HAN Guangchao,WANG Feng,ZHAO Heming,PENG Zhiling,LIU Jianxun

(School of Mechatronics Engineering, North University of China, Taiyuan 030051, China)

For terminal-sensitivity projectile(TSP)steady state scanning parameters were constant, and the law of scanning was certain, for the target with different parameters, it might lead to leakage scanning, and it even could not find the problem of the target in time, a method of the scanning angle self-adaptive adjustment of TSP based on target speed and length was proposed. The relation model of TSP and target was established, and then, the initial scanning angle as well as the steady state scanning angle was confirmed by MATLAB. The simulation results showed that: the method of self-adaptive adjustment presented in this paper could quickly adjust the scanning angle, and it improved scanning efficiency, and help it find the target in time. What’s more, the theoretical support and data reference were provided for the design of the TSP.

terminal-sensitivity projectile(TSP); scanning angle; self-adaptive adjustment; MATLAB

2016-01-22

國防科工局技術基礎項目資助

韓廣超(1989-),男,山東濟寧人,碩士研究生,研究方向:智能彈藥、探測制導與控制。

TJ410.1

A