基于交叉點的道路曲線化簡算法研究

李世寶，陳 通，劉建航，陳海華

(中國石油大學(華東) 計算機與通信工程學院，山東 青島 266580)

基于交叉點的道路曲線化簡算法研究

李世寶，陳 通，劉建航，陳海華

(中國石油大學(華東) 計算機與通信工程學院，山東 青島 266580)

現有的曲線化簡算法不能很好地化簡具有交叉路口的道路曲線，針對這一問題提出一種基于交叉點的道路曲線化簡算法。算法分為預化簡和修正化簡兩個階段：首先識別并得到曲線上的分段點，利用相鄰的分段點作為道格拉斯-普克算法的首尾點對曲線進行化簡，得到預化簡的結果；然后對于交叉點引入偏差閾值ε，通過判斷道路曲線交叉點與化簡后交叉點的距離與偏差精度ε的大小關系來確定該交叉點的化簡與保留，如果保留或者化簡后的道路曲線沒有交叉點那么將原交叉點作為分段點對此段曲線進行重新化簡。理論分析與實驗結果表明，文中算法能夠有針對性地保留或化簡道路交叉點以及保持曲線化簡后的形態特征。

交叉口；分段點；偏差閾值ε；道格拉斯-普克算法

近年來,隨著智慧城市、地理信息系統在各個領域的不斷深入，制圖綜合成為眾多學者研究的熱點[1]。曲線是地圖數據最基本的組成要素之一，在地圖數據中占據了很大的比例。因此，對于曲線的化簡一直是地圖自動綜合最重要的問題。在對線狀要素進行化簡時，首先要識別和提取曲線上重要的特征點，然后對曲線進行化簡。因為對于曲線化簡不僅僅只是關注曲線的壓縮率，曲線化簡后的形態也是衡量曲線化簡算法的一個重要指標。對于道路曲線，不僅僅曲線上重要的點為特征點，交叉點也是重要的特征點。因為交叉點是維持道路曲線交錯關系的點。

目前還沒有針對具有交叉點的道路曲線的成熟的化簡算法，傳統的曲線化簡算法主要有光柵法、垂距法[2]、角度限值法[3]、道格拉斯-普克算法[4]等，其中道格拉斯-普克算法是一種全局的化簡算法而廣泛用于曲線化簡中。該算法的主要思想是：設曲線是有P1,P2,P3,…,Pn等n個點組成，P1,Pn是曲線的首尾點。依次計算曲線上所有的點Pi(i=2,3,…,n-1)到首尾點P1,Pn構成的直線距離，記為Di(i=2,3,…,n-1),取其中最大的距離Dmax,如果Dmax小于設定的距離閾值D，則刪除P1，Pn內的所有的點，反之，則把最大距離對應的點作為分段點，把曲線分為兩段，然后在每一段上用同樣的方法進行處理，最后保留的點就是壓縮后的結果。該算法實現比較簡單，作為一種全局的曲線化簡算法能在化簡后一定程度上保持化簡后曲線整體形態，但是還存在很多缺陷：一些曲線上的點直接被化簡掉，其位置信息、重要程度并沒有考慮[5];化簡后曲線上一些重要的特征點丟失，不利于化簡后曲線整體的保持，道格拉斯-普克算法采用的是單一閾值，不能適應各種復雜的情況[6]；化簡后的曲線有可能相交[7]。因此，對于道格拉斯-普克算法，很多學者對其進行了改進：于靖等[8]提出了面向自然岸線抽稀的改進道格拉斯-普克算法，把曲線上重要的凸點作為曲線化簡的分段點，使用道格拉斯-普克算法進行化簡；張振鑫[9]等提出了多種數據化簡算法之間的對比，通過對比指出了數據化簡研究發展的趨勢；李朝奎等[10]以優化線狀要素的化簡綜合為目標，對道格拉斯-普克算法進行了改進，改進后的算法在保留了曲線的特征點后再對其進行化簡；巨正平等[11]提出了附有限制條件的逐點壓縮法，在滿足給定限差下能夠很好地考慮了化簡曲線之間的相互關系；張志偉等[12]通過建立距離閾值與化簡后的點數的最優擬合函數，分析擬合函數的性質確定距離閾值，從而更好地保留化簡后曲線形態，取得了比較好的化簡結果。

對具有交叉點的道路曲線進行化簡時，道路曲線的交叉點和化簡后保持曲線形態的點為重要的特征點，這兩類點在化簡時都要進行處理，上述對于曲線化簡算法的改進主要針對曲線上起伏比較大的特征點在化簡中的保留，并沒有考慮到除了這類特征點以外的點如道路交叉點的保留與化簡。雖然何海威[13]提出了一種采用彎曲避免化簡后道路的沖突，但僅僅是把所有的道路交叉點都保留下來，并沒有針對道路交叉點作進一步的分析與處理。本文針對目前具有交叉路口的道路曲線化簡的不足，提出了一種基于交叉點的道路曲線化簡算法。把道路曲線上特征點分為兩類，然后針對這兩類特征點分別進行處理，在保證化簡后道路曲線形態特征的同時保留符合實際需求的道路曲線交叉點。

1 改進的曲線化簡算法

1.1 算法的思想

對于包含多條道路曲線的復雜道路網，每一條道路曲線在空間數據庫中一般都是獨立存取。道路曲線之間存在著交錯關系，而交叉點是維持不同道路曲線拓撲關系的關鍵點，傳統的算法是化簡或者保留所有的道路交叉點。本文認為對于化簡后交叉點的偏移量小于偏差閾值的可以化簡。因此，對于一部分道路交叉點在不影響實際使用的情況下可以被化簡。若使用傳統的道格拉斯-普克算法對整段道路曲線進行化簡，單一的閾值不能保證曲線的各個部分都能得到最優化簡，而且也不能夠針對交叉點進行化簡。為了在化簡后能更好地保持道路曲線的形態特征和交叉點的位置，在化簡時應對這兩類點單獨進行處理，本文提出了基于交叉點的道路曲線化簡算法。算法主要包括：①選取曲線上重要的特征點；②選取和處理道路曲線交叉點。

1.2 曲線上重要特征點的選取與處理

對于曲線上重要的特征點，要選取對曲線整體形態影響比較大的點，采用基于m階鄰居坐標點的方法[14]來確定影響曲線形態的重要的特征點，以此為分段點，把道路曲線分成許多子曲線，在每段子曲線中把分段點作為道格拉斯-普克算法的首尾點進行化簡，利用基于最小二乘法的曲線擬合方法[15]得到每段子曲線中閾值與化簡后點數的關系，通過分析閾值與點數的擬合曲線，找到擬合曲線上曲率最大的點對應的閾值作為每段子曲線中最優閾值，分別對每段子曲線進行化簡。

1.3 交叉路口特征點的選取與處理

首先分析道路網中所有道路曲線的拓撲關系，獲取所有道路曲線的交叉點。然后設置滿足實際需求的偏差閾值ε，對于化簡后的道路曲線的交叉點分為兩種類型，第一種是化簡后的道路曲線有交叉點，另一種是化簡后的道路曲線沒有交叉點。

對于第一種化簡后的道路曲線有交叉點的類型，如果交叉點化簡前后的位移差D<ε,則化簡后交叉點不用處理，化簡掉該交叉點并不會對實際的使用造成較大的影響，而如果D>ε，交叉點被化簡會影響實際的使用需求，要對此交叉點進行處理。具體處理方法如圖1所示,P1(X1,Y1)、P2(X2,Y2)、P3(X3,Y3)、P4(X4,Y4)為預化簡過程的分段點，其坐標是已知的，P5(X5,Y5)為原始交叉路口，P6為化簡后道路曲線新的交叉路口，其坐標的計算方法為

通過求解方程組得到化簡后交叉點P6的坐標(X6,Y6)，進而得到化簡前后交叉點的偏移距離D,計算方法如下：

若D<ε,認為化簡后的交叉口滿足精度的要求，不需要對化簡后的交叉點做處理。若D>ε,則把原交叉點P5作為分段點，然后對由點P1，P2，P3，P4組成的曲線段P1P5，P2P5，P3P5，P4P5進行修正化簡，這樣就保證了道路曲線交叉點P5不被化簡。

圖1 化簡后曲線相交的交叉路口特征點的處理過程

對于第二種化簡后的道路曲線沒有交叉點的類型，則該交叉點不能被化簡，因為這種類型的交叉點是維持兩條道路曲線拓撲關系的關鍵點，如果被化簡兩條道路曲線就由相交變成了相離，導致原始到道路曲線之間的空間關系發生較大變化。如圖2所示,兩條道路曲線化簡后形成的線段P1P2,P3P4沒有相交，則以P5為分段點對此段曲線重新進行修正化簡，這樣交叉點P5就得了保留，道路曲線的拓撲關系也得到保持。

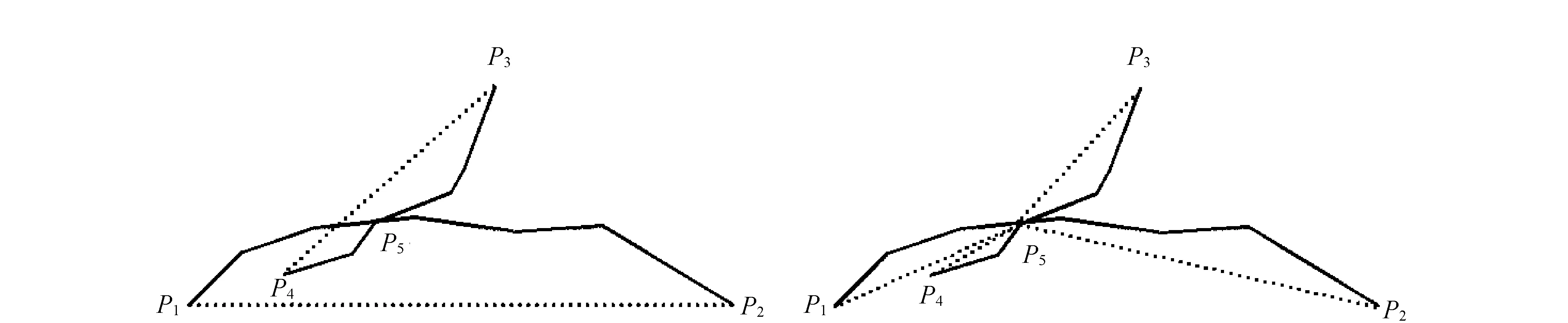
圖2 化簡后曲線不相交的交叉路口特征點的處理過程

2 算法實現

算法具體步驟如下：

1)針對道路網中的道路曲線進行相交和自交的拓撲分析，獲取到道路網中所有的交叉點。

2)在道路網中選取其中的一條道路曲線。然后從曲線的點Pi(i=2,3,…,N-1)中選取出特征點作為曲線的分段點。

3)以相鄰的分段點作為道格拉斯-普克算法的首尾點，利用基于最小二乘法的曲線擬合方法得到每一段曲線的最佳閾值，對分段后的曲線進行化簡。

4)重復步驟2)～4)把道路網中所有的道路曲線都化簡完畢，至此得到預化簡后的曲線。

5)分析交叉點所在線段化簡后是否相交，如果不相交執行步驟6)，如果相交則判斷道路曲線交叉點與化簡后交叉點的距離D與偏差閾值ε的關系，如果D<ε則此交叉點可以化簡掉，如果D>ε則此交叉點不能化簡，以此原交叉點為分段點，對相鄰的線段重新進行化簡。

6)化簡后的曲線不相交則交叉點不能被化簡，以原交叉點為分段點對相鄰的線段重新進行修正化簡。

7)重復執行步驟5)，直到所有道路交叉點處理完畢。

3 實驗與結果分析

為了驗證本文算法的有效性，在實驗中隨機選取一組道路曲線，利用本文所提算法與傳統的道格拉斯-算法進行化簡。通過化簡后的圖形來說明該算法的有效性。

圖3、圖4展示了傳統的道格拉斯-普克算法與本文算法對具有交叉路口的道路曲線的效果對比。圖3所示是傳統道格拉斯-普克算法對道路曲線的化簡結果，由實驗結果可知，傳統的道格拉斯-普克算法在對道路曲線進行化簡時，只是針對每一條道路曲線進行化簡，并沒有考慮道路曲線之間的拓撲關系，P1，P2，P3，P44個交叉點都被化簡，而且曲線上一些重要的特征點也沒有保留。同時由于交叉點P2被化簡，交叉點P2連接的兩條道路曲線由相交變為相離，道路曲線的拓撲關系發生了較大的改變。由此可見在對道路曲線進行化簡時，傳統的道格拉斯-普克算法不能滿足實際的應用需求。

圖3 傳統道格拉斯-普克算法化簡結果

圖4 本文算法化簡結果

圖4所示的是本文算法對道路曲線化簡的結果，由圖4(a)可知，當偏差閾值ε=1 mm時，交叉點P1，P3化簡之后的位置偏移小于ε，滿足偏差閾值的要求，因此，交叉點P1，P3被化簡。交叉點P2由于化簡后的道路曲線不相交而不能被化簡。交叉點P4由于化簡前后的距離大于偏差閾值ε而沒有被化簡。使用本文算法在ε=1 mm對道路曲線進行化簡后，交叉點P2，P4沒有被化簡，P1，P3被化簡掉，同時由于交叉點P2沒有被化簡兩條道路曲線化簡后的拓撲關系得到了保留。由圖4(b)可知，偏差閾值ε=2 mm，交叉點P1，P3，P4由于位置偏移都滿足精度要求而被化簡，交叉口P2由于化簡后道路曲線不相交而保留，維持了道路曲線之間的拓撲關系，同時曲線上一些重要的局部特征點也得

到了保留。因此，在使用本文算法對道路曲線進行化簡時，并不是保留所有的道路交叉點，而是引入偏差閾值ε概念，確定交叉點是否保留，在實際需求中可以通過設置偏差閾值ε的大小，以滿足不同的化簡精度需求。

4 結束語

對于道路曲線而言，道路曲線的交叉點作為維持道路拓撲關系的關鍵點，在對其進行化簡時，不能簡單地保留或化簡，應該單獨進行分析、處理。傳統的道格拉斯-普克算法在對道路曲線進行化簡時并沒有考慮到道路曲線交叉點的特殊性，不能滿足道路曲線實際的化簡需求。本文通過尋找曲線上的特征點作為分段點及引入偏差閾值ε，設計并實現了一種基于交叉點的道路曲線化簡算法，通過引入偏差閾值概念使得本文算法不同于傳統的算法對交叉點全部保留或者刪除，而是通過分析交叉點化簡后的特征選擇性的保留與化簡，使用本文算法對于密集道路網進行化簡時，能夠在保證道路曲線局部形態的前提下，科學有效地化簡或者保留交叉點，提升化簡的壓縮率。

[1] 蘇宏瑞,崔先國,彭玉艷.制圖綜合中基于中心地思想的線狀要素自動取舍算法研究[J].測繪科學,2007,32(1):40-42.

[2] 彭認燦,董箭,鄭義東,等.垂距法與道格拉斯-普克法刪除冗余頂點效率的比較[J].測繪通報,2010(3):66-67.

[3] 徐新.增強型矢量數據壓縮算法的設計與實現[J].計算機應用研究,2007,24(12):393-395.

[4] POIKER T,DOUGLAS D H.Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or its Caricature[J].Cartographica the International Journal for Geographic Information & Geovisualization,1973,10(2):112-122.

[5] TONG X,XU G.A new least squares method based line generalization in GIS[C]// Geoscience and Remote Sensing Symposium,2004.IGARSS’04.Proceedings.2004 IEEE International.IEEE,2004:2912-2915 vol.5.

[6] CARMONA-POYATO A,MADRID-CUEVAS F J,MEDINA-CARNICER R,et al.Polygonal approximation of digital planar curves through break point suppression[J].Pattern Recognition,2010,43(1):14-25.

[7] 張青年,廖克.基于結構分析的曲線概括方法[J].中山大學學報(自然科學版),2001,40(5):118-121.

[8] 于靖,陳剛,張笑,等.面向自然岸線抽稀的改進道格拉斯—普克算法[J].測繪科學,2015,40(4):23-27.

[9] 張振鑫,張維,劉嬪,等.矢量地圖數據簡化研究進展[J].測繪工程,2016,25(6)：10-14.

[10] 李朝奎,駱文芳,陳果,等.漸進式改進的線要素簡化算法探討[J].測繪科學，2015,40(11):123-126.

[11] 巨正平,王勇,郭廣禮,等.附有限制條件的逐點壓縮算法的設計與實現[J].測繪通報,2009(4):25-28.

[12] 張志偉,暴景陽,肖付民,等.基于Ping的Douglas-Peucker法抽稀閾值優化選取[J].海洋測繪,2015,35(2):9-12.

[13] 何海威,錢海忠,王驍,等.采用彎曲進行道路化簡沖突避免的方法[J].測繪學報,2016,45(3):354-361.

[14] 楊志堅.顧及局部特征的線狀要素制圖綜合[J].測繪科學,2016,41(4)：118-123.

[15] 王曉理,陳雙軍,魏斌,等.曲線擬合的Douglas-Peucker算法閾值優化選擇[J].測繪科學技術學報,2010,27(6):459-462.

[責任編輯：劉文霞]

A road curve simplification algorithm based on intersection point

LI Shibao，CHEN Tong，LIU Jianhang，CHEN Haihua

(College of Computer and Communication Engineering，China University of Petroleum，Qingdao 266580，China)

The existing algorithms on curve simplification can’t simplify the road curve with intersections.To solve this problem,this paper proposes a road curve simplification algorithm based on intersections.The first stage is called pretreatment stage,which identifies the segmentation points of a curve,and treats the adjacent segmentation points as beginning and end points of Douglas Peucker algorithm to get the simplified pretreatment results.The second stage is called correction simplification stage,which determines the simplification or deviation of intersections,by introducing a deviation threshold ε,and comparing it with the distance between before-simplification and after.If the intersections are retained or there are no intersections after simplification,redo the simplification by using the previous intersections as segmentation points. Theoretical analysis and experimental results show that the proposed algorithm can retain or simplify the adjacent points purposefully,meanwhile keeping the morphological characters of curves after simplification.

intersection feature point;segmentation point;deviation threshold;Douglas-Peucker algorithm

著錄：李世寶，陳通，劉建航，等.基于交叉點的道路曲線化簡算法研究[J].測繪工程，2017，26(7)：1-4，11.

10.19349/j.cnki.issn1006-7949.2017.07.001

2016-07-18

山東省自然科學基金面向項目(ZR2014FM017);中央高校基本科研業務費專項資金資助項目(15CX05025A);青島市科技創新計劃(15-9-80-jch);青島市黃島區科技發展計劃項目(2014-1-45)

李世寶(1978-)，男，副教授，碩士.

P208

A

1006-7949(2017)07-0001-04