把握直觀與抽象的平衡點——小學一年級“解決問題”教學之我思

裘飛云

【摘 要】本文從三個方面結合教學實際探討小學低段數學問題解決中如何處理好抽象與直觀的關系，認為問題解決過程中需要做到圖思結合，由扶到放培養學生的思維能力，提升數學思維水平。

【關鍵詞】低年級數學；解決問題；抽象；直觀；扶放結合

我國著名的數學家華羅庚說：“數缺形時少直觀，形少數時難入微，數形結合百般好。”一語中的說明了抽象數學與直觀圖形的關系。就低年級學生而言，他們的思維以直觀形象思維為主，但這也不等于低年級數學除了直觀教學，就不需要培養學生的抽象思維能力。在此，筆者結合教學實際探討小學低段數學問題解決中如何處理好抽象與直觀的關系。

一、探究：以適度直觀為手段逐步過渡到抽象

新教材的“問題解決”特別重視問題情境的創設，教師需要引導學生及時抓住問題的主線，分析其中的數量關系，盡早架起問題的結構模型。

比如在教學“一共可以站進多少個女生”問題時，我們出示情境圖，有學生不加思考地回答女生肯定也是10個，因為他發現這樣排隊過程中女生與男生是“一男，一女”依次排列的，而有的學生則認為是5個，因為他發現每兩個男生對應一個女生，所以理解上就出現了分歧。此時我們可以分兩步與學生進行研究：

明確問題：在10個男生中間隔可以插入多少名女生？探查條件：什么是每相鄰的兩個男生中間插入一個女生。澄清問題的主線：這里我們需要分析的是每兩個男生對應一個女生，還是一個男生對應一個女生呢？還是都不是？此時教師不便把自己的理解強加給學生，可以對上述錯誤理解的學生進一步提問：

（1）假如現在有三位男生，（大屏幕上出示三位男生站位圖），請問此時每兩位男生之間可以插入多少個女生？（學生想象回答，教師出示圖解。）

（2）如果現在我這兒有4位男生呢？（教師指示在講臺前可以站的位置，但并沒有讓學生上臺示范，學生憑想象作答）

（3）假如現在有5位男生呢？7位呢？那10位呢？你發現了什么規律？為什么？

上述討論過程中，教師能逐步過渡，使學生在頭腦中樹立所研究問題的表象后，再一步步移走直觀物，讓學生通過想象來完成問題，最后還讓學生總結出問題解決的模型，并理解是為什么，這樣有就使抽象思維能力的培養落實顯得非常實際而到位。

二、操作：以具體材料為依托學習制作抽象圖形

在小學低年級教學中，需要為學生能夠畫抽象的幾何理解圖（線段圖，方框圖，圓形圖等）做一些適當鋪墊。如“用以5以內的減法解決問題”。

（1）看式畫圖： 出示“5-3=”， 請學生畫圖來表示，學生感到困難。

（2）教師表演： 出示5張動物卡片，獎給專心聽課的小朋友3張，此時其它學生豎起了耳朵，教師問：現在還有幾張？

（3）學生操作： 拿出相同的5張圓形卡片（也可以是動物模型），拿走3個， 還剩下2個。

（4）學生口頭表述：今天，我表演了……我發現……還剩下……。

（5）討論： 剛才大家的表演中，5、3、2分別表示什么？

（6）畫圖： 把大家剛才演的情節用圖形來表示。

上述教學過程中，學生看減法算式直接畫圖是有難度的，因為此時學生不但對減法的意義還沒有真正領悟，而且還缺少直觀物的依賴來進行思考，或者說過去雖然有過直觀物，但現在頭腦中早已經忘卻了這個表象，所以此時提出讓學生來直接畫圖其實是“殘酷”地“將”了學生一“軍”，使他們處于無從下手的境地，讓他們處于一種暫時的焦慮狀態，有助于激發他們的學習動機。下一步，教師帶領大家從頭開始領悟前邊已經學過的減法所代表的現實問題，這里教師巧妙地把減數化為了對學生的獎勵（三張動物卡片），使得學習動機得到進一步調動，而且使問題再度回到直觀。接下來由學生來進行操作時，學生操作的物體可以自由選擇，這就擺脫了前邊教師單獨作主決定實物的情況，使得思維的抽象程度有一定提升。讓學生口述這一步，學生需要憑記憶與語言來進行思考完成，抽象程度更深了。

三、理解：借助直觀圖示在對應中感悟數理

運用畫圖策略來解決問題，一直是數學學習中的基本策略。畫圖策略具有深入淺出的特點，一方面畫圖可以對題目意思進行簡化，對不同數量關系進行直觀的比較，有助于學生盡快理清數量關系。畫圖的目的并不是只為畫圖，主要在于導思，所以教學引導的過程寧可先慢后快，防止生吞活剝。

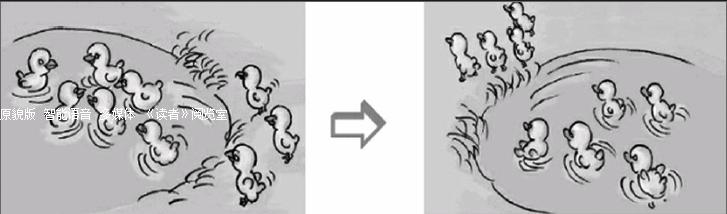
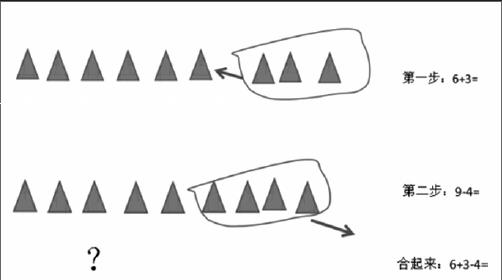
如教學“加減混合運算及問題解決”時，我們出示的例題為：池塘里原來有6只小鴨，來了3只，又走了4只，現在還有多少只小鴨？

在學生認識主題圖后，首先要求學生邊打手勢邊敘述圖意；然后要求學生用小三角形表示這個變化過程，并在圖上找到數字所代表的部分（如圖），在分步列式中要他們找到數字對應的圖形。由于有了這種對應，步步落實，他們的理解就比較深刻，在事后的看文字應用題列式中就明顯提高了正確率。

“萬丈高樓平地起”，小學低年級數學中的問題解決，特別要注意落實好直觀與抽象的關系，既要防止一下子過于抽象造成學生理解上的難度，也要防止直觀到底而阻礙學生抽象思維能力的培養。