對小學數學該教什么的思考

鄭泳濠

【摘要】對于數學的課程目標，不同時期有不同的理解，目標不同，教學思路也不同，學生的收獲自然也不同.下面以三次圓的面積公式推導的教學為例，談談一線數學教師對“教什么”的思考的重要性，它是所有教學行為的基礎，比對“怎么教”的思考更重要.

【關鍵詞】小學數學；圓的面積

圓的面積計算是小學六年級上學期的教學內容，這是學生學習的第一種曲線圖形的面積計算，教學內容包括對圓面積概念的理解、公式的推導、運用公式求圓的面積、環形的面積等.這部分內容的學習相當重要，是滲透把曲線圖形轉化成直線圖形來研究的方法的好題材，也是滲透極限思想的好題材.

一教圓的面積公式推導——借助多媒體課件

教學目標：認識圓面積的概念，推導圓面積公式，運用公式計算圓面積.圓面積公式的推導是一節課的一部分內容.過程簡介如下：

1.學生自學教材.

2.課件演示：把一個圓平均分成16份，用紅色表示其中的8份，用藍色表示另外的8份，然后把兩個8份移動拼成一個近似的長方形.課件形象生動，在適當時候還有聲音提示引起注意.

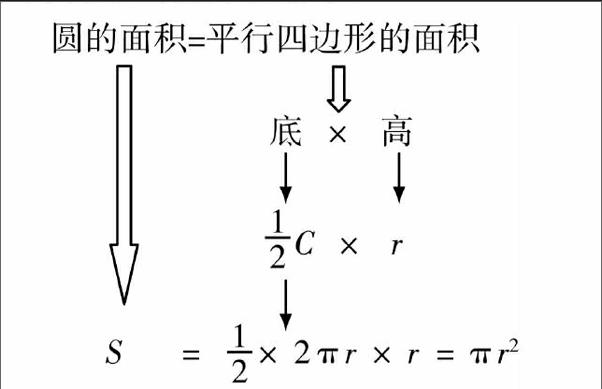
3.教師引導學生觀察拼出來的長方形的長、寬分別是多少，邊引導回答邊完成下面板書：

由于課前的預習，加上教師的暗示引導，學生（特別是學優生）一般都能按教師的意愿講出以上的推導過程.圓面積公式的推導就大功告成了.

效果情況反饋：

在運用圓的面積公式解決問題的過程中，發現不少學生記不住公式或與圓的周長公式混淆.而且大部分學生面對以下填空題一臉茫然，能夠填對的只有那么幾名學優生.

如果把圓分成（）等份，可以拼成一個近似平行四邊形.拼成的這個平行四邊形的（）相當于圓（）的一半，這一半用字母表示是（），它的（）就是圓的（），所以圓的面積公式是（）.

二教圓的面積公式推導——以學生為主體，動手操作

教學目標：認識圓面積的概念，推導圓面積公式，運用公式計算圓面積.圓面積公式的推導是一節課的一部分內容.過程簡介如下：

1.布置課前預習.課前引導學生看教材的推導過程，然后布置學生回家按教材要求完成推導過程，具體的預習要求如下：

（1）畫兩個一樣大小的圓，剪下來（也可以用附頁中的圓）.

（2）把其中一個圓平均分成若干份（說明分的份數越多越好，最好是偶數份）.

（3）按順序把各份編號.

（4）把這些近似的等腰三角形拼成一個近似的長方形（也可以拼成其他學過的圖形）.

2.課堂上推導公式的過程：

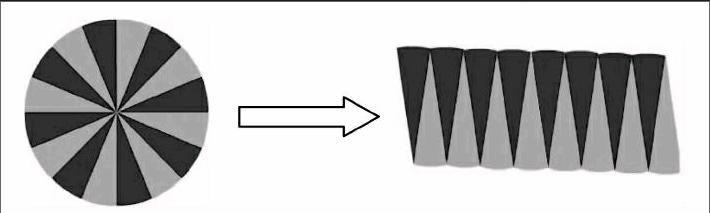
（1）同位合作，按書上的方法把圓轉化為平行四邊形，教師巡視完成情況.大部分學生都能順利拼出這樣的圖：

（2）讓學生以小組為單位，看有什么發現，如果要求這個近似平行四邊形的面積，該怎么求？

（3）由學生自由匯報各小組的研究成果（在學生匯報前選一個拼得好的圖貼在黑板上），教師根據匯報整理板書（具體跟“一教”中的板書相同）.經過幾名學生的發言，把書上的推導過程講清楚.

（4）看著板書，再讓學生把思維過程理順，并引導學生總結學習方法，使學生知道可以把曲線圖形轉化為直線圖形來研究.

（5）教師巡視時發現，有些學生把圓分成了8等份、32等份……，于是讓不同分法的學生都展示自己拼的平行四邊形，結果發現，分的份數越多，每一份就會越細，拼出來的圖形就會越接近于長方形.這樣用課堂生成的具體實例來滲透抽象的極限思想.

（6）演示課件，加深認識.

（7）推導方法拓展.教師提問：除了上面的拼法，還有別的拼法嗎？

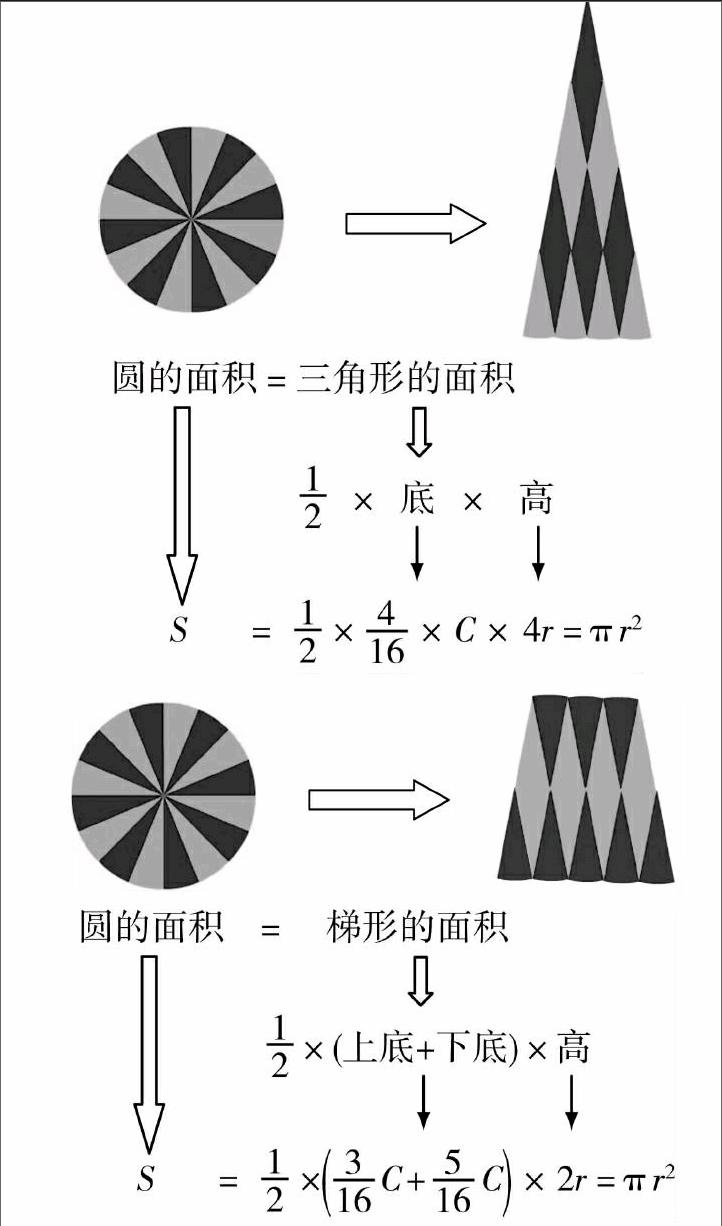
教師巡視發現，有個別學生拼出了三角形或梯形.教師再提出問題：假如這樣拼，能推導出圓的面積公式嗎？學生再度進入了探究學習中.

下面是學生拼出的兩個圖和推導過程.

有一名學生還推導出用直徑來計算的圓面積公式：S=114πd2.

（8）出示以下填空題，大部分學生能填對.

如果把圓分成（）等份，可以拼成一個近似平行四邊形.拼成的這個平行四邊形的（）相當于圓（）的一半，這一半用字母表示是（），它的（）就是圓的（），所以圓的面積公式是（）.

（9）總結.告訴學生，今天所用數學思想方法是把未知的問題轉化成已知問題來研究（即把曲線圖形轉化為直線圖形來研究），把學生的空間觀念引入一個新的領域.

效果情況反饋：

由于這節課讓學生合作探究的時間比較長，因此，沒完成計劃內容——用公式計算圓的面積，但學生對圓面積公式的理解還是比較深入的.后續的應用練習中，學生把面積與周長混淆的現象不多.但是，當堂的教學內容沒有完成，而能接受推導公式拓展部分的又只是少數學生.

三教圓的面積公式推導——關注數學思考方法

教學目標：探索并掌握圓的面積計算公式；體會和掌握轉化、推理、極限等數學思想方法；獲得數學活動的經驗.計劃用兩節課來達成目標.

第一節課：圓面積公式推導的準備課.

完成幾個任務：

1.引導學生回顧以前研究多邊形面積的方法.

2.引導學生思考圓的面積如何用轉化的方法來研究.

3.引導看明白教材的剪拼方法.

4.出示教師預先分好的圓，引導認識分出來的小扇形（近似的等腰三角形）.

5.布置預習任務：

（1）畫兩個一樣大小的圓，剪下來（也可以用附頁中的圓）.

（2）把其中一個圓平均分成若干份（說明分的份數越多越好，最好是偶數份）.

（3）按順序把各份編號.

（4）看懂書中的推導公式方法，并自己嘗試完成推導過程.

（5）除了書中的方法，還有沒有其他方法？

第二節課：圓面積公式推導課.

1.四人小組交流課外拼成的近似長方形，說說怎樣根據拼出的圖形算出圓的面積，教師巡視，了解學生完成情況.

2.請一些小組匯報教材上的推導方法，教師在學生回答的過程中給予適當的引導.

3.除了教材中的方法，還有沒有其他方法？四人小組交流一下.

教師巡視發現，有個別學生拼出了三角形或梯形（如“二教”中的圖），但還不會計算拼出的圖的面積；有個別學生認為不需要拼，直接求出一個小扇形（近似的等腰三角形）的面積再乘分出的個數即可.

教師及時肯定這些學生的想法，展示他們拼出的三角形和梯形，并提出問題：拼出的三角形或梯形的面積跟圓的面積有什么關系？能不能求出三角形（或梯形）的面積，然后求出圓的面積？

4.同位合作，嘗試求拼出的三角形或梯形的面積；如果直接求出一個小扇形（近似的等腰三角形）的面積再乘分出的個數又該怎么算？

5.提問交流計算過程，教師做適當的引導.

6.利用多媒體課件的演示，展示把圓平均分成32份、64份、128份甚至更多份的情況，讓學生直觀地看到圖形的變化趨勢，體會極限思想.

效果情況反饋：

這樣教學的效果非常好，在之后的應用練習中，全班學生基本都不會把周長和面積混淆，“磨刀不誤砍柴工”，雖然這里多用了一節課，但學生真正理解了圓的面積，運用公式更順暢，節省的就不是一節課了.到后面學習環形、外圓內方和外方內圓時，前面兩節課所滲透的思想方法、所積累的活動經驗起到了作用，明顯感覺學生能積極參與探究過程，并知道如何去研究.而且中等以上的學生都能正確解答以下與圓的面積公式推導有關的題目：

題1：圖1中圓的周長是12.56厘米，圓的面積正好等于長方形的面積，求陰影部分的面積.

題2：在圖2中，已知長方形的面積與圓的面積相等，一只螞蟻沿著陰影部分的邊沿，從A點出發，按A→B→C→D的順序，最后回到A點.如果這只螞蟻每分鐘爬20 cm，一共要用多少分鐘？

分析反思三次教學圓的面積公式推導，我有以下收獲.

1.對“教什么”的思考非常重要.

“一教”“二教”只關注知識與技能層面的目標，目標是讓學生會做題，但由于沒有真正理解知識的本質，所以往往事與愿違；“三教”更關注了數學思考、問題解決層面的目標，更符合《義務教育數學課程標準（2011年版）》的理念，更能發揮數學的育人功能，更有利于培養學生的數學素質，做題能力自然得到提升.

2.“怎么教”的效果取決于“教什么”的正確定位.

“一教”和“二教”教學方式完全是不同的，但由于“教什么”沒改變，所以即使把學生當成了學習主體，教學效果也還是不理想.“二教”和“三教”形式上是一樣的，都是提供機會讓學生動手操作，自主探究學習，但由于“教什么”的定位不同，教學過程的側重點也有所不同，因此，收到不同的效果.具體體現在：

（1）轉化思想需要有意滲透.“二教”和“三教”的整個過程都滲透了轉化思想，但“三教”的滲透是教師的有意行為，因此，效果更明顯.

（2）推理能力需要搭建階梯.“二教”的推理能力訓練完全靠學生自己的原有水平，因此，能真正接受多種推導方法的只有個別學優生；而“三教”，由于教師有意識要讓學生積累數學活動的經驗，要訓練學生的推理能力，因此，專門安排了一節準備課，為學生的推理搭起了階梯，使學生的推理成為可能.堂上還充分利用學生學習過程生成的資源，給學生再次提供推理能力訓練的機會，起到鞏固和拓展教材上方法的作用，對已掌握教材上方法的學生是一次運用推理方法的過程，對還不掌握教材上方法的學生則再次提供學習素材讓其學習，因此，能使更多的學生受益.

（3）極限思想需要形象演示.極限思想對于小學生來說比較抽象.“二教”是利用學生資源來讓學生感受，素材來自于學生，使學生感到親切，效果也不錯，但對于極限思想的理解還不夠形象，因此，“三教”專門利用多媒體課件的演示，更形象，效果更好.

（4）動手操作的目標是積累活動經驗.“二教”中，教師把動手操作的目標指向拼出三個圖，教師的提問是：“還有別的拼法嗎？”而“三教”中，教師把動手操作作為活動的基礎，活動的目標指向推導圓的面積計算公式，體驗操作活動的價值，有效地積累活動經驗，教師的提問是：“還有沒有其他方法？”兩個不同的提問，給了學生不同的思考方向，效果自然就不同.

數學新課程實施應以學生數學素質的養成為核心目標，課堂教學中學生數學活動經驗的獲得是學生數學素質養成的必要條件.而數學活動經驗需要在“做”的過程和“思考”的過程中積淀，是在數學學習活動過程中逐步積累的.因此，作為小學數學教師，一定要研究教材，把“教什么”弄清楚，明確每個章節內容所肩負的責任，用好數學素材組織學生開展數學活動，提供機會讓學生獲得活動經驗，從而提高數學素養.