三角形“心”問題的向量解法
2017-06-15 14:15:46江蘇省灌云高級中學222200
數理化解題研究 2017年1期
江蘇省灌云高級中學(222200)
張永樓●
三角形“心”問題的向量解法
江蘇省灌云高級中學(222200)
張永樓●
向量是代數與幾何的一個完美結合.三角形的四個“心”即外心、內心、重心和垂心,是三角形問題中經常考查的一個知識點,也是較容易被混淆的.將三角形中的邊與角的關系轉化為向量運算,將會使問題變得更簡單易解,本文將研究如何利用向量方法來解決三角形的“心”問題.
一、向量與三角形的“垂心”





評注 在幾何問題中,線線垂直可以轉化為向量數量積等于零,反之,向量數量積等于零也可以轉化為線線垂直.
二、向量與三角形的“外心”


評注 向量平方等于向量模的平方,在解題中可以通過平方將向量的模轉化為向量的運算來解答.
三、向量與三角形的“重心”




所以A,D,G三點共線,所以,點G在BC邊的中線上.
同理,點G也在邊AB,AC的中線上.
所以點G是△ABC的重心.

四、向量與三角形的“內心”




又因為λ∈[0,+),所以向量)與向量為共線向量,且方向相同.
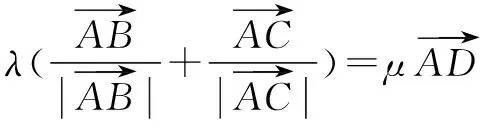


所以點P在AD上移動.即P點的軌跡一定通過△ABC的內心.
G632
B
1008-0333(2017)01-0038-01

