向量背景下的最值問(wèn)題舉隅

安徽省宿州市埇橋區(qū)祁縣中學(xué)(234115)

張 剛●

向量背景下的最值問(wèn)題舉隅

安徽省宿州市埇橋區(qū)祁縣中學(xué)(234115)

張 剛●

向量是高中數(shù)學(xué)中非常重要的內(nèi)容，也是高考的必考考點(diǎn).它是溝通代數(shù)、幾何、函數(shù)、不等式等各部分?jǐn)?shù)學(xué)知識(shí)的一種工具.而以向量為背景的最值問(wèn)題，因題型靈活、多變，知識(shí)點(diǎn)考查多，在歷年各地高考題、模擬題中屢見(jiàn)不鮮.如果能夠恰當(dāng)靈活地選擇方法，就能達(dá)到化難為易，優(yōu)化解題過(guò)程，提高解題效率的目的.本文結(jié)合幾道實(shí)例，拋磚引玉如下，供大家參考.

1.構(gòu)造線性規(guī)劃求最值

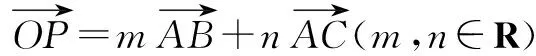
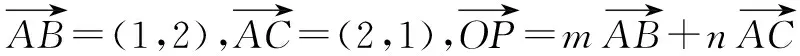
令y-x=t,顯而易見(jiàn)，當(dāng)直線y=x+t過(guò)點(diǎn)B(2,3)時(shí)，t取得最大值1，故m-n的最大值為1.

評(píng)注 對(duì)此類問(wèn)題，一般思路是：設(shè)出動(dòng)點(diǎn)坐標(biāo)，利用向量的相關(guān)知識(shí)將參數(shù)用動(dòng)點(diǎn)坐標(biāo)表示出來(lái)，寫(xiě)出目標(biāo)函數(shù)，化為簡(jiǎn)單的線性規(guī)劃中的最值問(wèn)題求解.

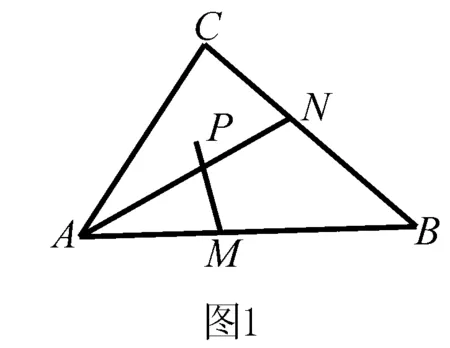
2.構(gòu)造可行域，利用幾何圖形關(guān)系求最值

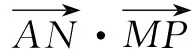
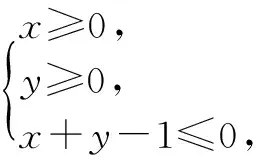
評(píng)注 目標(biāo)函數(shù)最終由動(dòng)點(diǎn)P的坐標(biāo)表示的，那么點(diǎn)P的活動(dòng)范圍也就是可行域，就是條件中的幾何圖形及其內(nèi)部區(qū)域.

3.構(gòu)造一元目標(biāo)函數(shù)求最值

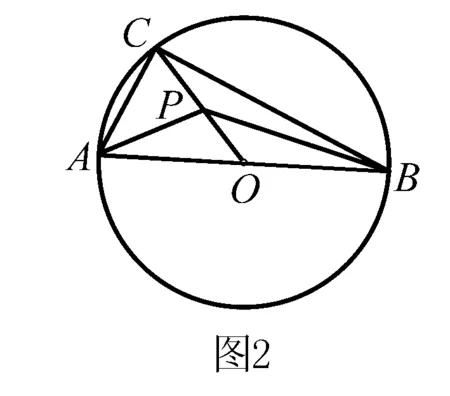
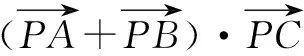
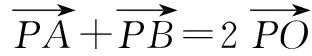
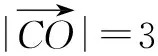
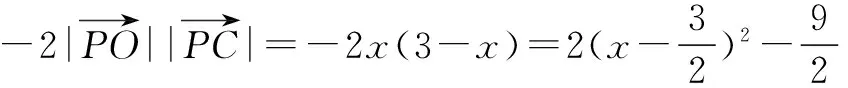
評(píng)注 將數(shù)量積的運(yùn)算轉(zhuǎn)化為求一元二次函數(shù)的最值，用配方法獲解.

4.構(gòu)造多元目標(biāo)函數(shù)求最值

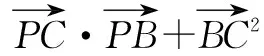
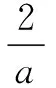
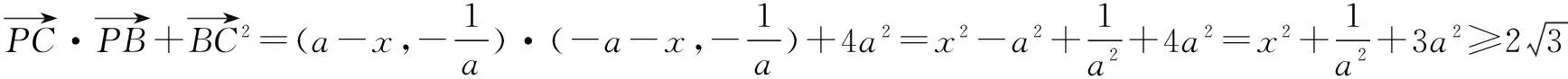
評(píng)注 對(duì)與向量運(yùn)算有關(guān)的多元參數(shù)的最值問(wèn)題，常通過(guò)向量運(yùn)算轉(zhuǎn)化為多元函數(shù)的最值問(wèn)題，再利用消元、換元等手段轉(zhuǎn)化為一元函數(shù)的最值問(wèn)題，或多次利用基本不等式或用柯西不等式求其最值，其中多次利用基本不等式求最值時(shí)，注意“一正二定三等”的原則.

5.構(gòu)造代數(shù)坐標(biāo)法求最值

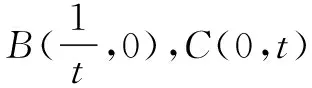
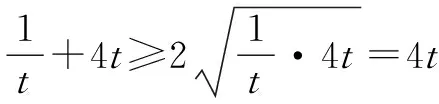
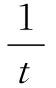
評(píng)注 本題有向量垂直的明顯信息，易建立平面直角坐標(biāo)系，將平面向量數(shù)量積的最值問(wèn)題，轉(zhuǎn)化為一元對(duì)勾函數(shù)的最值問(wèn)題，巧用均值不等式獲解.

6.構(gòu)造三角坐標(biāo)法求最值

例6 (2015 上海卷)已知平面向量a,b,c滿足a⊥b且{|a|,|b|,|c|}={1,2,3},則|a+b+c|的最大值是____.

解 因?yàn)閍⊥b，{|a|,|b|,|c|}={1,2,3},

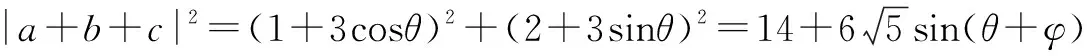
7.構(gòu)造-|a||b|≤a·b≤|a||b|求最值

例7 (2012 安徽卷)若平面向量a,b滿足：|2a-b|≤3,則a·b的最小值是____.

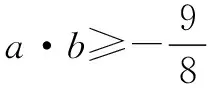
評(píng)注 由定義a·b=|a||b|cos〈a,b〉可得|a·b|≤|a||b|,即-|a||b|≤a·b≤|a||b|,a·b≤|a|·|b|即為對(duì)a·b放大，-|a|·|b|≤a·b,即為對(duì)a·b縮小.

8.構(gòu)造||a|-|b||≤|a±b|≤|a|+|b|求最值

例8 已知平面向量a,b,c滿足|a|=1,|b|=2,|c|=2,|a+b|=|a-b|, 則|a+b+c|的最大值是____.

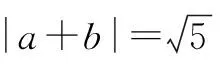
評(píng)注 對(duì)于|a+b|的最值問(wèn)題，常利用三角不等式的向量形式||a|-|b||≤|a±b|≤|a|+|b|求最值.

9.構(gòu)造模長(zhǎng)為軌跡是圓問(wèn)題求最值

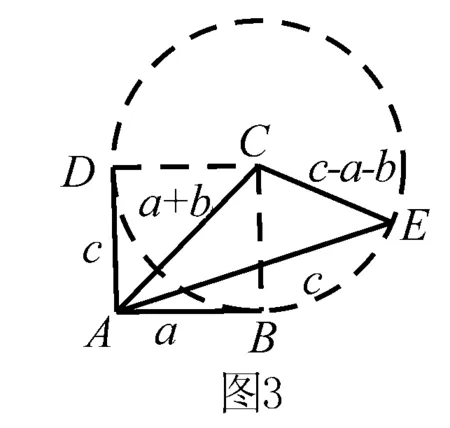
例9 已知a,b是單位向量，a·b=0，若向量c滿足|c-a-b|=1，則|c|的取值范圍是____.

評(píng)注 在同一平面內(nèi)，圓是到定點(diǎn)距離等于定長(zhǎng)的點(diǎn)的集合，也是相對(duì)弦的張角為定角的點(diǎn)的集合.

總之，只要善于巧妙地利用題目的已知條件，結(jié)合向量的相關(guān)知識(shí)，運(yùn)用構(gòu)造思想，將向量的最值問(wèn)題轉(zhuǎn)化為線性規(guī)劃、函數(shù)、不等式、圓等數(shù)學(xué)最值問(wèn)題，即可迎刃而解，達(dá)到化難為易，優(yōu)化數(shù)學(xué)問(wèn)題的目的.

G632

B

1008-0333(2017)01-0003-02