試題是怎樣煉成的
——一類基于合情推理的圓錐曲線試題命制

福建省泉州第五中學(362000)

楊蒼洲●

試題是怎樣煉成的
——一類基于合情推理的圓錐曲線試題命制

福建省泉州第五中學(362000)

楊蒼洲●

合情推理有“歸納”和“類比”兩種推理模式，這種推理是建立在觀察、實驗的基礎上，通過“類比”來產生“聯想”，或者通過“歸納”來進行“猜想”，是一種“發現未知”的思維形式.

在解析幾何的某些問題中，我們常常可以通過類比、歸納，從中發現“圓、橢圓、雙曲線、拋物線”的一些共同性質.因此，基于“圓錐曲線”，交匯考查“合情推理”成為命制“解析幾何”試題的一種常見命題手法.這樣的試題設計精彩紛呈，往往成為一份試卷的亮點所在.下面筆者略舉數例，與讀者共賞.

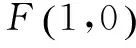
(Ⅰ)求軌跡C的方程；

分析與解 本小題主要考查拋物線的定義與標準方程、直線與圓錐曲線的位置關系等基礎知識，考查推理論證能力、運算求解能力，考查化歸與轉化思想、數形結合思想、特殊與一般思想等．

(Ⅰ)易得曲線C的方程為y2=4x．

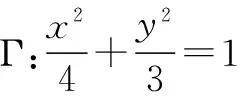
(Ⅰ)求曲線Γ的方程；

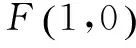
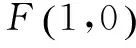
分析與解 本小題主要考查圓的方程與性質、橢圓的標準方程與性質、直線與圓錐曲線的位置關系等基礎知識，考查推理論證能力、運算求解能力，考查化歸與轉化思想、數形結合思想、特殊與一般思想等．

(Ⅱ)設三角板的直角頂點放置在圓O的圓周上的點N(a,b)處，則a2+b2=2，又設三角板的另一條直角邊所在直線為l′．

(ⅰ)當a=1時，l′與曲線Γ有且只有一個公共點．

(Ⅰ)拖動點S，發現當xS=4時，yS=4，試求拋物線E的方程；

(Ⅱ)設拋物線E的頂點為A，焦點為F，構造直線SF交拋物線E于不同兩點S、T，構造直線AS、AT分別交準線于M、N兩點，構造直線MT、NS．經觀察得：沿著拋物線E，無論怎樣拖動點S，恒有MT∥NS．請你證明這一結論．

分析與解 本小題主要考查拋物線的標準方程、直線與圓錐曲線的位置關系等基礎知識，考查推理論證能力、運算求解能力，考查化歸與轉化思想、分類與整合思想、數形結合思想等．

(Ⅰ)易得拋物線E的方程y2=4x．

(Ⅰ)求橢圓E的方程；

(Ⅱ)給出命題：“已知P是橢圓E上異于A1,A2的一點，直線A1P,A2P分別交直線l：x=t(t為常數)于不同兩點M、N，點Q在直線l上.若直線PQ與橢圓E有且只有一個公共點P，則Q為線段MN的中點”，寫出此命題的逆命題，判斷你所寫出的命題的真假，并加以證明;

(Ⅲ)試研究(Ⅱ)的結論，根據你的研究心得，在圖2中作出與該雙曲線有且只有一個公共點S的直線m，并寫出作圖步驟(注意：所作的直線不能與雙曲線的漸近線平行) .

分析與解 本小題主要考查橢圓的標準方程與性質、直線與圓錐曲線的位置關系等基礎知識，考查推理論證能力、運算求解能力，考查化歸與轉化思想、數形結合思想、特殊與一般思想等．

(Ⅱ)逆命題：“已知P是橢圓E上一點，直線A1P、A2P分別交直線l：x=t(t為常數)于M、N兩點，若Q為線段MN的中點，則直線PQ與橢圓E有且只有一個公共點P”，為真命題．

(Ⅲ)如圖，①任作一條直線n垂直于實軸；②作直線A1S、A2S分別交直線n于I、J兩點；③作線段IJ的中點V，則直線SV即為所求的直線m．

(Ⅰ)求雙曲線C的方程；

(Ⅲ)試推廣(Ⅱ)中的命題，寫出關于圓錐曲線(橢圓、雙曲線、拋物線)統一的一般性命題(不必證明)．

分析與解 本小題主要考查合情推理、直線、橢圓、雙曲線、拋物線等基礎知識，考查推理論證能力、運算求解能力，考查數形結合思想、化歸與轉化思想、特殊與一般思想．

上述幾個試題的求解過程，要求學生經歷逆向思維、類比推理、直觀感知、操作確認、思辨論證，度量計算的心路歷程.雖然試題情境新穎，但是其本質依然是研究曲線軌跡，求解直線與拋物線位置關系等問題.因此在復習中，我們要深化對圓錐曲線方程的理解，進一步熟練掌握待定系數法、定義法等求軌跡的常規方法，進一步掌握直線與拋物線位置關系的一般解題方法，要注意總結試題的規律，如：直線與圓錐曲線位置關系中的相交弦問題在高考中經常被設計成考題，在解決此類問題時，我們常聯立方程組，利用韋達定理，進行“設而不解”來解題.

G632

B

1008-0333(2017)01-0028-03