過三點如何作多面體的截面

華南師范大學(xué)附屬中學(xué)(510630) 羅碎海

過三點如何作多面體的截面

華南師范大學(xué)附屬中學(xué)(510630) 羅碎海

目前流行的高考二輪復(fù)習(xí)資料《創(chuàng)新設(shè)計》P36【例1-2】:如圖,在棱長為6的正方體ABCD?A1B1C1D1中,E,F分別在C1D1與C1B1上,且C1E=4,C1F=3,連接EF,FB,DE,BD則幾何體EFC1?DBC的體積為( )

A. 66 B. 68 C. 70 D. 72

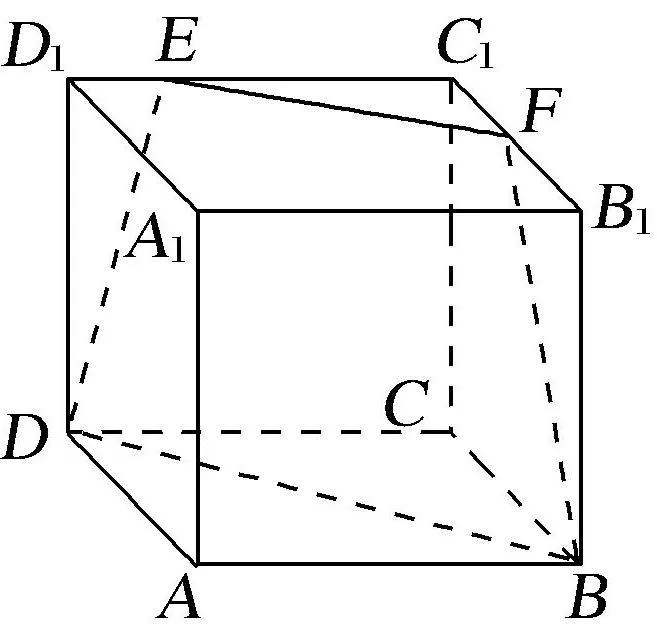
圖1

這是一道錯題,點E、F、B、D四點不在同一面內(nèi),無法求體積．但書中給出答案,而且有些學(xué)生也做出答案A．由此可見,無論是做題人還是制題人都在立體幾何作圖問題上有所欠缺,該問題值得研究．

在平面幾何中,尺規(guī)作圖是妙趣橫生、引人入勝、很有思維挑戰(zhàn)的一類問題,特別是幾何作圖三大不能問題(三等分角;立方倍積;化圓為方)更是登峰造極之題,引無數(shù)英雄競折腰,大大推動了數(shù)學(xué)的發(fā)展．而在立體幾何中因存在諸多不便,作圖問題就不作為主要問題來研究,但畫空間幾何體的截面也是一件很有意義之事．雖在高考考試中,對立體幾何作截面的要求不高,考試說明中明確指出:只要求會畫出給出全部頂點的多面體截面．但對于立體幾何的學(xué)習(xí),作圖問題(畫截面)是概念、定理深刻理解與應(yīng)用的基本標志之一,更是培養(yǎng)學(xué)生空間想象能力及創(chuàng)造性思維能力的不可多得的素材．

由于不在同一直線上的三點確定一個面,所有問題就歸于已知三點畫截面.畫截面就是找到截面與多面體的面的交線,找交線就是找到同一面上兩個點．所以作截面常用的根據(jù)是以下6個定理或公理:

(1)(公理)同一平面內(nèi)的兩條直線,若不平行必然相交．

(2)(公理)如果一條直線上的兩點在一個平面內(nèi),則這條直線在這個平面內(nèi)．

(3)(公理)兩個平面如果有一個公共點,則它們有且只有一條通過該點的公共直線．

(4)(定理)過兩平行線或兩相交直線有且只有一個平面．

(5)(定理)三個平面兩兩相交,它們的交線或交于一點或兩兩平行．

(6)(定理)兩個平行平面與第三平面相交,則它們的交線平行．

具體的方法思路有:直接連線,延長線段,作平行線,作輔助面等．有時可能需要射影,有時還可借助代數(shù)特別是向量來計算．以下我們從最簡單的多面體—長方體為主分析各種情況并總結(jié)其方法．

一、已知三點在長方體的棱上的情況

問題1.1已知三點分別在長方體三條棱上,三棱為順次相交的長、寬、高,如何作過此三點的截面?

例1 長方體ABCD?A1B1C1D1,P、Q、R分別為D1A1、A1A、AB上任意一點．作出過點P、Q、R的平面α截長方體ABCD?A1B1C1D1的截面．

分析同一面上兩點連線延長與棱相交,連續(xù)進行．

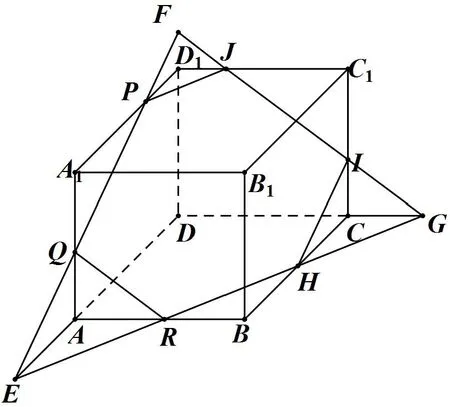
圖2

作法如圖2,連PQ,交DD1、DA延長線于F、E;連E、R交BC、DC延長線于H、G;連F、G,交D1C1、C1C于J、I;連PQRHIJP為所作截面．

(說明:截面有可能是三角形、四邊形、五邊形、六邊形)

評述面上有兩點,連線就是交線．

問題1.2 已知三點分別在長方體三棱上,其中有兩棱相交,如何作過此三點的截面?

例2 長方體ABCD?A1B1C1D1,P、Q、R分別為C1D1、A1A、AB上任意一點．作出過點P、Q、R的平面α截長方體ABCD?A1B1C1D1的截面．

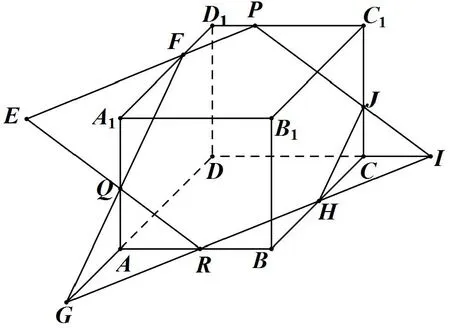
圖3

作法如圖3,連RQ,交B1A1延長線于E;連E、P交A1D1延長線于F;連F、Q,交DA延長線于G;連G、R交BC、DC延長線于H、I;連I、P交CC1于J;連PFQRHJP為所作截面．

評述點為兩線相交所得,線為兩面相交所得,這樣認識例1、例2思想方法相同．以上作圖主要用到定理(1)、(2)、(3)．

問題1.3 已知三點分別在長方體的三條棱上,三棱相互異面,如何作過此三點的截面?

例3 長方體ABCD?A1B1C1D1,P、Q、R分別為D1A1、AB、CC1上任意一點.作出過點P、Q、R的平面α截長方體ABCD?A1B1C1D1的截面．

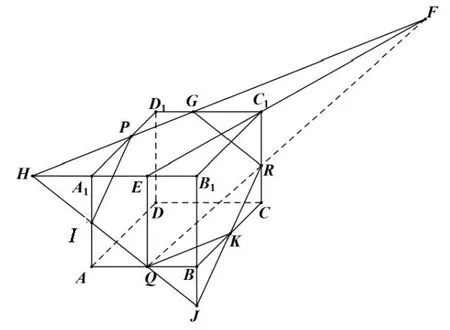
圖4

作法如圖4,作QE//BB1交A1B1于E,則QE、RC1確定一個平面;連EC1,QR交于點F;連FP交C1D1、B1A1延長線于G、H;連HQ交A1A、B1B延長線于I、J;連JR交BC于K．連KRGPIQK為所作截面．

評述本作法用到定理(4)、(5),關(guān)鍵是由Q、R找到點F,使點F與點P在同一面內(nèi)(過點Q、R作點P所在面的垂線)．反思兩個問題:

①若作QE//AD交DC于E,下一步如何作?

②若作PE//AA1交AD于E,下一步如何作?

問題1.4 (特殊問題)已知三點分別在長方體的共頂點的三條棱上,如何作過此三點的截面?

答直接連每兩點,得到的三角形就是截面．

問題1.5 (特殊問題)已知三點分別在長方體的三條互相平行棱的上,如何作過此三點的截面?

答直接連線,作平行線即可．(用到(5)、(6))

問題1.6 已知三點分別在長方體的三條棱上,其中只有兩條棱平行,如何作過此三點的截面?

(平行棱上兩點連線,仿例1,略)

二、已知三點不在長方體棱上而在表面上的情況

問題2.1 三點在長方體的共頂點的相鄰的三個面上,如何作過此三點的截面?

例4長方體ABCD?A1B1C1D1,P、Q、R分別為面ABB1、BCC1、A1B1C1上任意一點．作出過點P、Q、R的平面α截長方體ABCD?A1B1C1D1的截面．

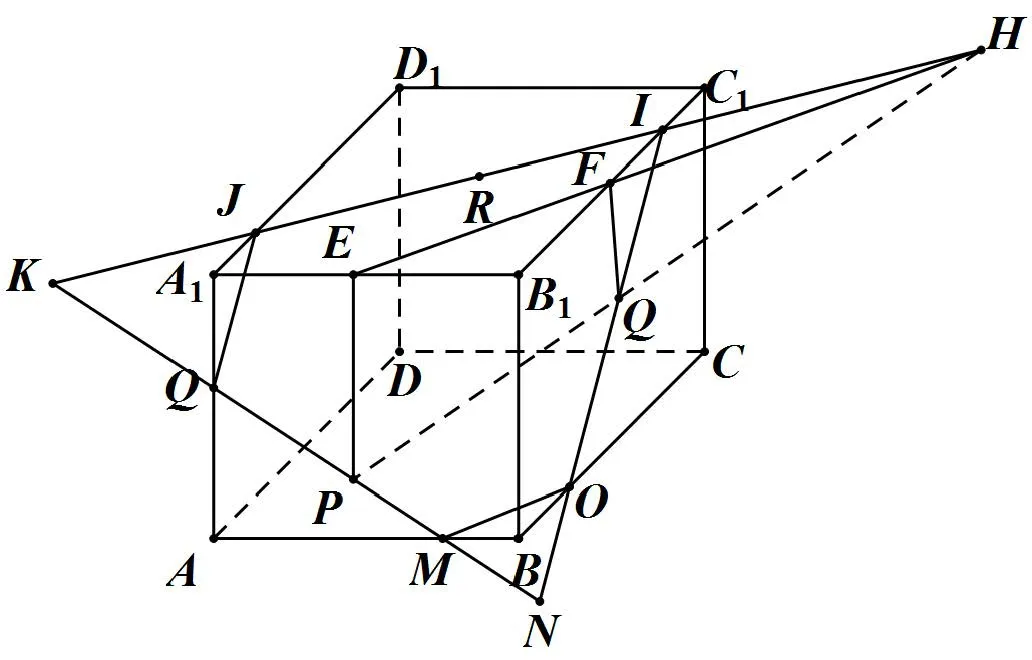
圖5

作法如圖 5,過P作PE⊥A1B1于E,過Q作QF⊥B1C1于F,連EF、PQ交H,連HR交B1C1、D1A1、B1A1于I、J、K,連KP交A1A、AB、B1B延長線于L、M、N,連NI必過Q與BC交于點O．連IJLMOI為所作截面．

評述本作法用到定理(4)、(5),其主要思路是:由P、Q找到點H,使點H與點R在同一面內(nèi)(過點P、Q作點R所在面的垂線)．

思考在例4的作法中,若PE=QF,如何作圖?

問題2.2 三點在長方體的相鄰(不共點)的三個側(cè)面上,如何作過此三點的截面?

例5長方體ABCD?A1B1C1D1,點R、P、Q分別為面AA1D1D、A1ABB1、B1BCC1上任意一點．作出過點R、P、Q的平面α截長方體ABCD?A1B1C1D1的截面．

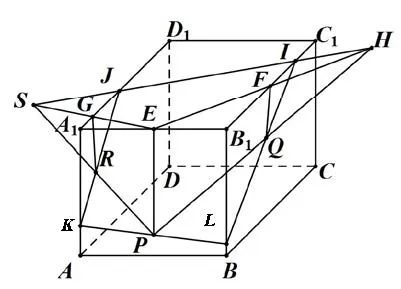
圖6

作法如圖6,分別過點R、P、Q作平面A1B1C1D1的垂線,交棱A1D1、A1B1、B1C1于G、E、F,連EF、PQ交于點H,連PR、EG交于點S;連SH交A1D1、B1C1于J、I;連JR交A1A于K,連KP交B1B于L,連LI必過Q;連JKLIJ為所作截面．

評述關(guān)鍵是三側(cè)面上的點向底面作垂線;平行線確定平面;找到一個面上的兩點．

三、其它多面體的截面作圖

有了以上的基礎(chǔ),其他問題就容易了．諸如:已知的三點中有些在長方體的面上(非棱)、有些在棱上的情況就可以解決．進一步可以處理其它多面體(一般棱柱＼棱錐、棱臺等)的截面問題．

例6已知三點P、Q、R分別在四棱錐O?ABCD的三條側(cè)棱OA、OB、OD上,求作過點P、Q、R的截面(假設(shè)PQ、PR都不與底面平行)．

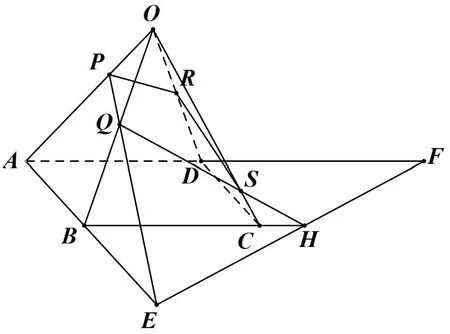
圖7

作法

① 連PQ與AB交于點E,連PR交AD于點F;

② 連EF交BC于H,連QH與OC交于S;

③ 連RS,則四邊形PQSR為所作截面．

(說明:若H在線段BC內(nèi),則截面為五邊形.)

立體幾何作截面是要求比較高且比較困難問題,本文主要以長方體為載體分析探究過已知三點做截面的思維方法,以期達到空間想象能力的再提高,奠定解決未來問題的基本思想方法．為了對以上問題類型與作圖方法更全面的掌握,編寫以下練習(xí),加以鞏固提高．

練習(xí)

1.長方體ABCD?A1B1C1D1,P、Q、R分別為B1C1、A1A、AB上任意一點.作出過點P、Q、R的平面α截長方體ABCD?A1B1C1D1的截面．

2.長方體ABCD?A1B1C1D1,P、Q、R分別為C1C、A1A、AB上任意一點.作出過點P、Q、R的平面α截長方體ABCD?A1B1C1D1的截面．

3.正三棱柱ABC?A1B1C1,P、Q、R分別為AA1、BB1、A1C1上任意一點.作出過點P、Q、R的平面α截正三棱柱ABC?A1B1C1的截面．

4.正四棱錐S?ABCD,P、Q、R分別為AD、BC、SC上任意一點．作出過點P、Q、R的平面α截正四棱錐S?ABCD的截面．

5.正三棱錐S?ABC,P、Q、R分別為SA、BC、SC上任意一點．作出過點P、Q、R的平面α截正三棱錐S?ABC的截面．