空間想象與構造圖形交替思維
——幾則空間想象能力的考查到了極致的關于球的立幾題

云南省玉溪第一中學(653100) 武增明

空間想象與構造圖形交替思維
——幾則空間想象能力的考查到了極致的關于球的立幾題

云南省玉溪第一中學(653100) 武增明

在高考、競賽中,經常出現短小精悍、新穎別致、設計獨特、能力立意高、很靈活的關于球的立幾小題,以考查同學們的空間想象能力和構造圖形的能力,可以說達到淋漓盡致的程度.現采擷幾例加以分析,以期對提高同學們的空間想象能力和構造圖形的能力有所幫助,同時也供同仁教學參考.

例1 (2011年全國卷II理科11(文12)題)已知平面α截一球面得圓M,過圓心M且與α成60°二面角的平面β截該球面得圓N.若該球面的半徑為4,圓M的面積為4π,則圓N的面積為( )

A. 7πB. 9πC. 11πD. 13π

解設球面的球心為O,圓M和圓N的公共弦為BC.過點M作AM⊥BC,因為MO,MN,MA都垂直BC,所以MO,MN,MA共面.因為∠NMA=60°,∠OMA=90°,所以∠OMN=30°,如圖1.在Rt△OMC中,

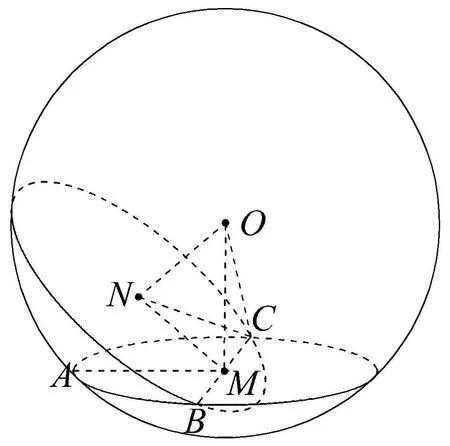
圖1

評注(1)通過空間想象,畫出符合題意的示意圖,是快速破解此題的一個重要關鍵.(2)圓N的劣弧BC在球面內,但這與解答此題無關.

例2 已知球O的半徑為2,圓O1,O2,O3為球O的三個小圓,其半徑分別為若三個小圓所在的平面兩兩垂直且公共點為P,則OP=____.

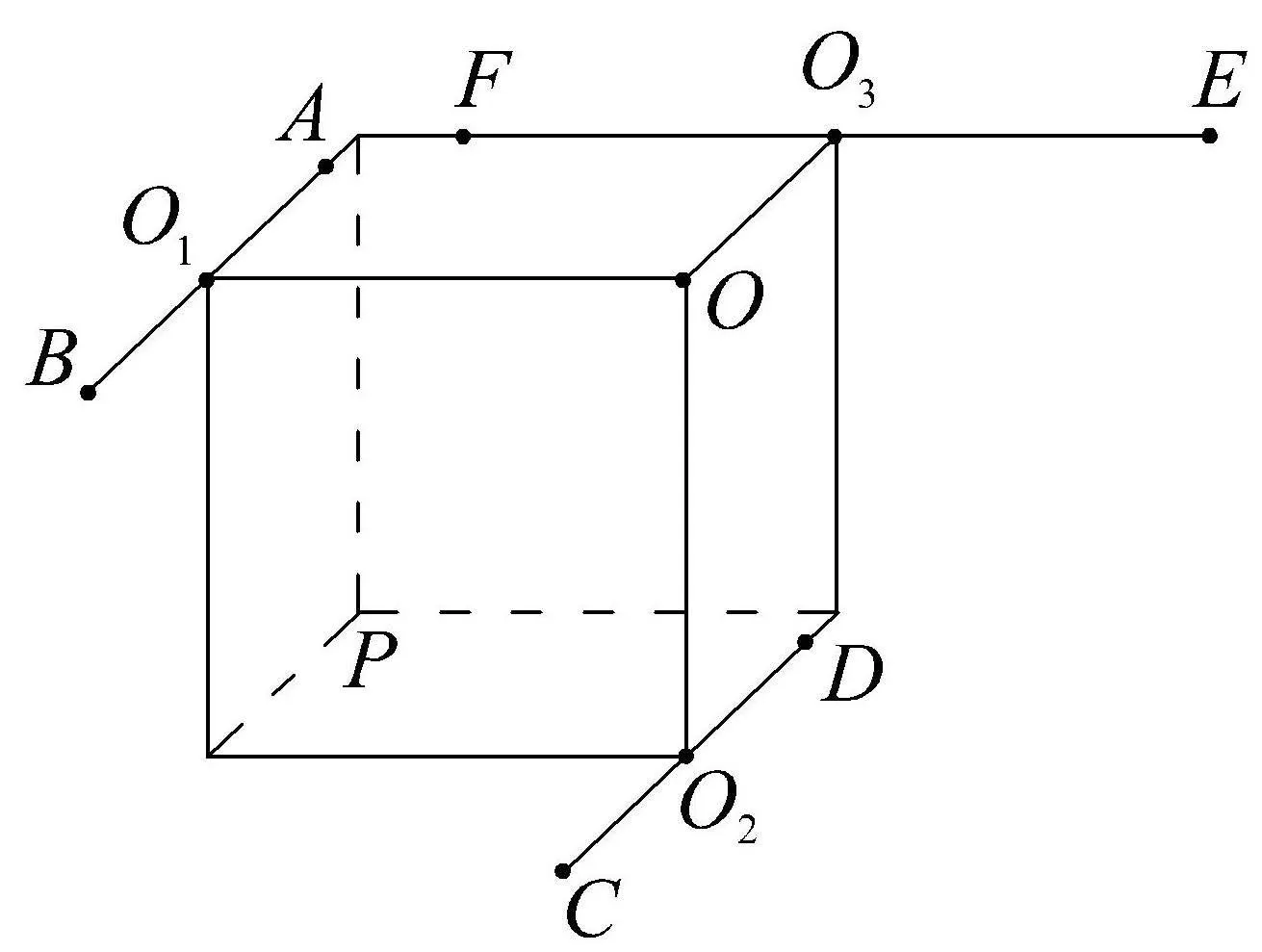
圖2

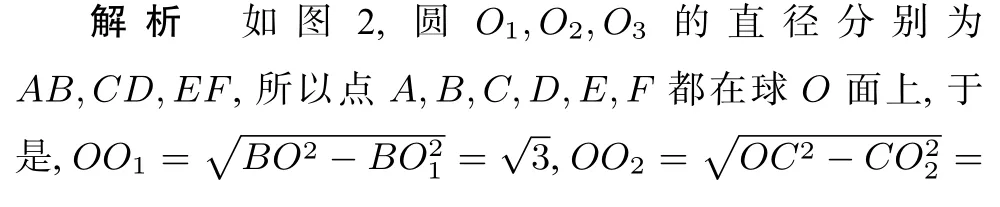
評注(1)此題中的點P在球O面外.(2)此題要求我們要有較強的空間想象能力,這樣才能把立體圖呈現在頭腦中,由此并畫出相應的立體圖,進而得以獲解.(3)要直接畫出立體實圖,困難很大.

例3 在一個棱長為6的正四面體紙盒內放一個正方體,并且能使正方體在紙盒內任意轉動,則該紙盒內正方體棱長的最大值是___.

分析此題若直接求解,困難非常大,若借助正四面體的內切球來解答,會收到意想不到的效果.其思路是,先求出正面體的內切球的半徑,然后再求球的內接正方體的棱長,這時的正方體的棱長最長,即為盒內正方體棱長的最大值.

解設正四面體各面的面積為S,高為h,其內切球的半徑為R,則由三棱錐的等體積法得,

設此正四面體內切球的內接正方體的棱長為a,則即紙盒內正方體棱長的最大值是

評注(1)想到正四面體內切球的內接正方體的棱長最長,是破解此題的關鍵.(2)解答完此題后,我們更進一步掌握球內接的長方體或正方體在其球內可以任意轉動.

例4(2010年全國高中數學聯賽新疆維吾爾自治區預賽試題)已知半徑為r的球和半徑為R的兩個相切的球都相切,且它們都與大小為60°的二面角的兩個半平面相切,則

解析設半徑為R的兩個球的球心為O1,O2,半徑為r的球的球心為O3,通過空間想象,把符合題設的立體圖呈現在腦海中,由此畫出簡要的立體圖,如圖3.依題意知,點O1,O2,O3確定的平面平分已知二面角,且點O1,O2,O3到二面角的距離分別為2R,2R,2r.過點O3作O3H⊥O1O2,垂足為H,則O3H=2R?2r,O1O3=O2O3=R+r.所以O1H=HO2=R.在Rt△O1HO3中,

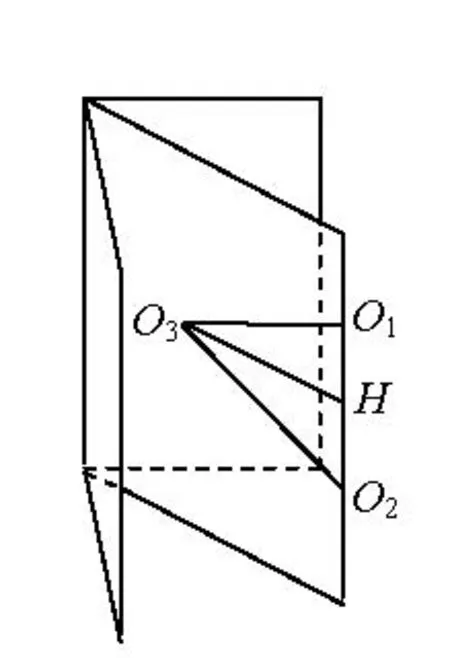
圖3

評注要把符合題意的立體圖全部畫出來,困難是巨大的,也沒有這個必要.

在立體幾何學習中,需要我們有較好的空間想象能力,這樣我們才能把立體圖呈現在頭腦中,進而畫出簡要的立體圖或詳細完整的立體圖,才有可能獲解.簡單地說,解決型如上面所例舉到的那類問題的有效思維途徑是空間想象與構造圖形交替思維.

例5 棱長為2的正方體ABCD?A1B1C1D1的所有頂點均在球O的球面上,E,F,G分別為AB,AD,AA1的中點,則平面EFG截球O所得圓的半徑為____.

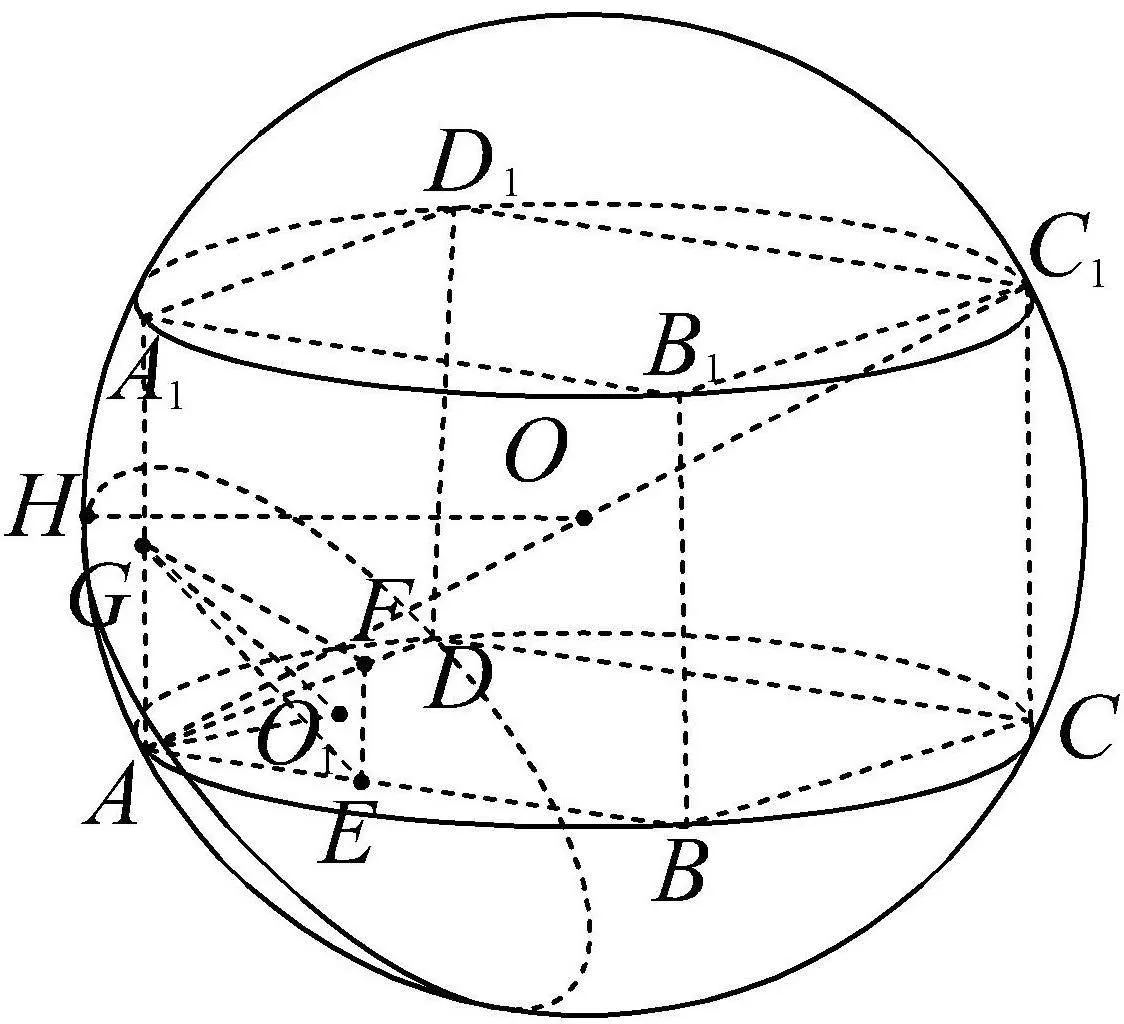
圖4

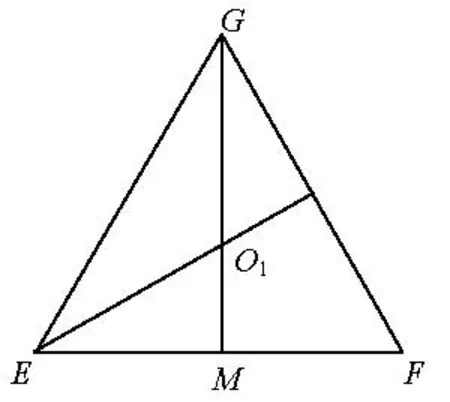
圖5

解析設球O的半徑為R,則依題意得(2R)2= 22+22+22?R2=3.

評注(1)要把符合題意的立體圖全部畫出來,困難是很大的,也沒有這個必要.(2)在解答此題時,需要一半空間想象一半畫圖.(3)在解答此題時,要想到平面EFG截球O所得圓與等邊三角形EFG的外接圓是同心圓.

例6 三個半徑都是1的球放在一個圓柱內,每個球都接觸到圓柱的底,則圓柱的底面圓半徑的最小值是( )

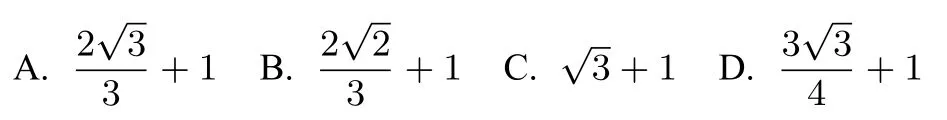
解析問題可轉化為,三個半徑都是1的小圓放在一個大圓內,三個小圓兩兩外切,求大圓半徑的最小值.

當且僅當三個小圓兩兩外切,且與大圓內切時,大圓半徑最小,設此時大圓的半徑為R.設三個球的球心分別為O1,O2,O3,即三個小圓的圓心分別為O1,O2,O3,設大圓的圓心為O,如圖6.大圓的圓心O是等邊三角形O1O2O3的外心(“四心”重合),于是故選A.

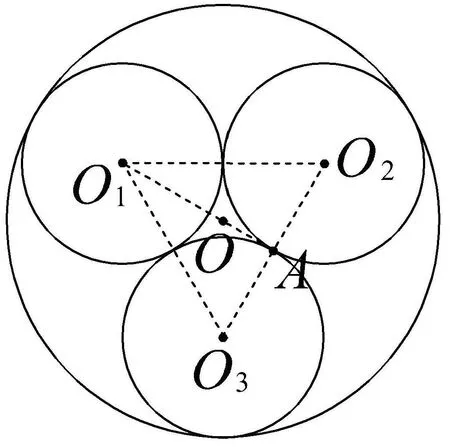
圖6

評注(1)要把立體圖畫出來,很難,也沒有這個必要.(2)解答此題時,關鍵是通過空間想象后把問題作等價轉化.

例7 (2016年高考全國卷III文科11(理科10))在封閉的直三棱柱ABC?A1B1C1內有一個體積為V的球.若AB⊥BC,AB=6,BC=8,AA1=3,則V的最大值是( )

解析首先考慮球與封閉的直三棱柱ABC?A1B1C1的三個側面相切,此時球的半徑R等于直角三角形A1B1C1的內切圓的半徑,如圖7,這時R=2.而AA1=3,因此,若R=2,則封閉的三棱柱ABC?A1B1C1容納不下球,從而考慮球與封閉的三棱柱ABC?A1B1C1的兩底面都相切,此時球的半徑R最大為這時球的體積為故選B.

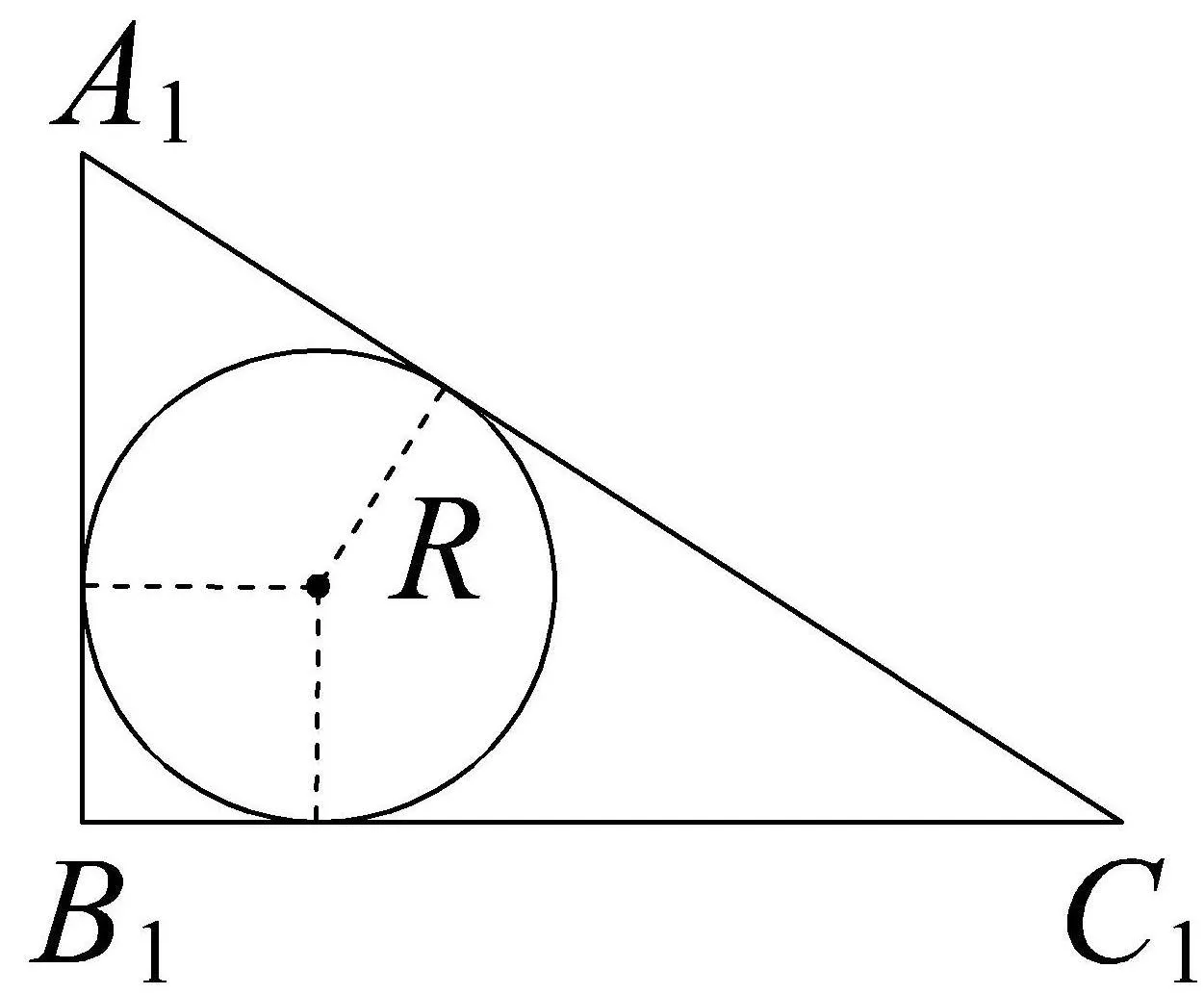
圖7