珠海市斗門區第一中學(519100) 唐學寧

例析函數選擇壓軸題的解題策略

珠海市斗門區第一中學(519100) 唐學寧

函數選擇壓軸題由于其“數式”的變換及“形”的千姿百態,展示了它特有的數形結合思想,對培養學生的觀察力,訓練思維的廣闊性與深刻性發揮其特有的作用.然而,高考函數選擇題的得分率歷年來都較低,尤其是函數選擇題中的壓軸題得分率更是如此.為此,筆者通過對近年來的試題進行分類解析,希望能給讀者一些啟示.

一、巧選特殊函數 用特殊值法

在函數問題中,如果已知條件中含有某些不確定的量,但題目暗示答案可能是一個定值時,可以將一般函數取一個特殊的函數來求出這個定值,從而達到簡化求解過程的目的.

例1已知函數f(x)在R上的導函數為f′(x),若f(x)＜2f′(x)恒成立,且f(ln4)=2,則不等式f(x)＞的解集是( )

A. (ln2,+∞) B. (2ln2,+∞)

C. (?∞,ln2) D. (?∞,2ln2)

例2定義在R上的偶函數f(x)的導函數為f′(x).若對任意的實數x都有2f(x)+xf′(x)＜2恒成立,則使x2f(x)?f(1)＜x2?1成立的實數x的取值范圍為( )

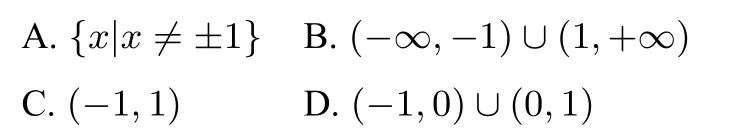
分析因為函數f(x)為偶函數,我最快想到的函數是f(x)=0,計算f′(x)并代入驗證,發現完全滿足條件2f(x)+xf′(x)＜2,因此可以直接取f(x)=0.

解令f(x)=0,計算可知滿足條件,則要解的不等式x2f(x)?f(1)＜x2?1變為x2?1＞0,解之得(?∞,?1)∪(1,+∞),答案為B.

點評聯系已知條件和結論,構造特殊函數是解高中數學函數選擇題中的巧妙方法,如果在題目中給出奇偶性與單調性,往往取多項式函數做為特殊函數.

二、精挑選擇項值 用排除法

在函數選擇題中,如果一時沒有什么好的思路,也可以從選擇支中挑選一些值,代入題目中去驗證,如果滿足條件,則表示該選擇支有可能就是要選的答案,這種方法對一些難、偏、繁問題有奇效.

例3已知函數f(x)=aex?x2?(3a+1)x,若函數f(x)在區間(0,ln3)上有極值,則實數a的取值范圍是( )

分析觀察四個選擇項,可以發現,如果我們取a=?2代入驗證,可以一次性排除兩個答案.

解令a=?2,則f(x)=?2ex?x2+5x,得f′(x)=?2ex?2x+5,故f′(0)=?2+5=3＞0,f′(ln3)=?2×3?2ln3+5＜0,知函數f(x)在區間(0,ln3)上有極值,a=?2滿足條件,排除C、D兩個答案.觀察A、B,發現只須選a=?1進行驗證即可.此時f(x)=?ex?x2+2x,f′(x)=?ex?2x+2,而f′(0)=?1+2=1＞0,f′(ln3)=?3?2ln3+2＜0,也滿足條件.因此選A答案.

點評用排除法的一般情況下要做兩次,第一次在四個選擇項里選值時,應選兩個包含這個值,另兩個不包含這個值,這樣就能排除兩個答案;第二次選值時怎么簡單怎么選.

例4若函數f(x)=ex(sinx+acosx)在上單調遞增,則實數a的取值范圍是( )

A.(?∞,?1] B.(?∞,?1) C.[1,+∞) D.(1,+∞)

分析四個選擇支這么有規律,不使用排除法都可惜了.取a=1可以一次排除兩個答案.

解令a=1,則

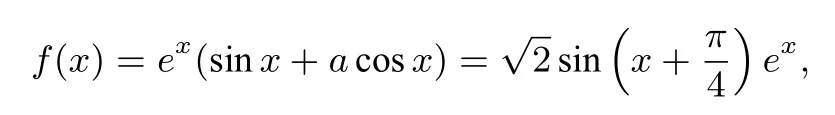
點評有些同學可能觀察到C、D答案全正,而A、B有正有負,因此先選a=0,然后再選a=1,這其實也是一樣.在使用排除法過程中,選值非常重要,選值好,能簡化運算,方便解題,選值不好,可能讓整個題目繁難復雜不可計算.

三、細畫函數圖像 用數形結合法

“數”與“形”是數學的基本研究對象,它們之間存在著對立統一的辯證關系.數形結合思想,就是將抽象的數學語言與直觀的圖形結合起來,通過對圖形的認識、數形轉化,以提高思維的靈活性、形象性、直觀性,使問題化難為易,化抽象為具體.

例5.已知函數若關于x的方程f(f(x))=a存在2個實數根,則a的取值范圍為( )

A. [?24,0) B. (?∞,?24)∪[0,2)

C. (?24,3) D. (?∞,?24)∪[0,2]

分析方程f(f(x))=a是一個嵌套函數,f(x)是一個分段函數,如果直接去求f(f(x))的解析式,難度將相當大.而如果畫出f(x)的圖像,根據圖像分析結果,難度將小很多.

解畫出y=f(x)的圖像如圖所示,觀察四個選擇項,可選取a=?6.如果a=?6滿足條件,則可排除B、D,否則排除A、C.由f(f(x))=?6,得f(x)=?8或f(x)=2,而f(x)=?8有兩個根,f(x)=2有一個根,共3個根,因此不滿足條件,排除A、C.觀察B、D,選a=2,f(f(x))=2得f(x)=0,而當f(x)=0時只有一個根x=?2(x=1是空心點),所以應選答案B.

點評本題采用了數形結合與排除法,簡單易行,比使用直接求函數f(f(x))的解析式要簡單得多.其中選a=?6是為了更好的計算出根.

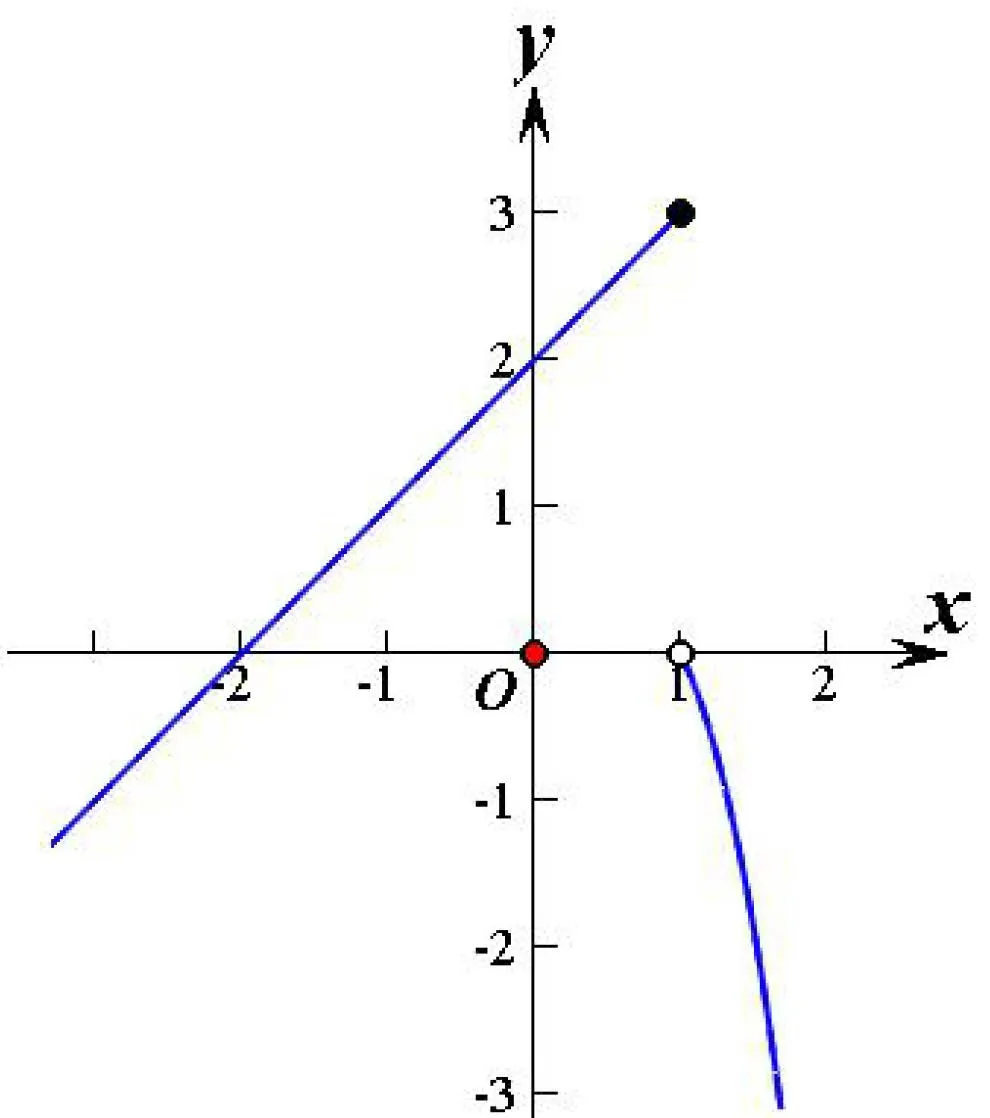
圖1

例6已知函數則下列關于函數y=f[f(x)]+1的零點個數的判斷正確的是( )

A. 當k＞0時,有3個零點;當k＜0時,有2個零點

B. 當k＞0時,有4個零點;當k＜0時,有1個零點

C. 無論k為何值,均有2個零點

D. 無論k為何值,均有4個零點

分析方程y=f[f(x)]+1是一個嵌套函數,求其解析式有一定難度,因此采用數形結合法.

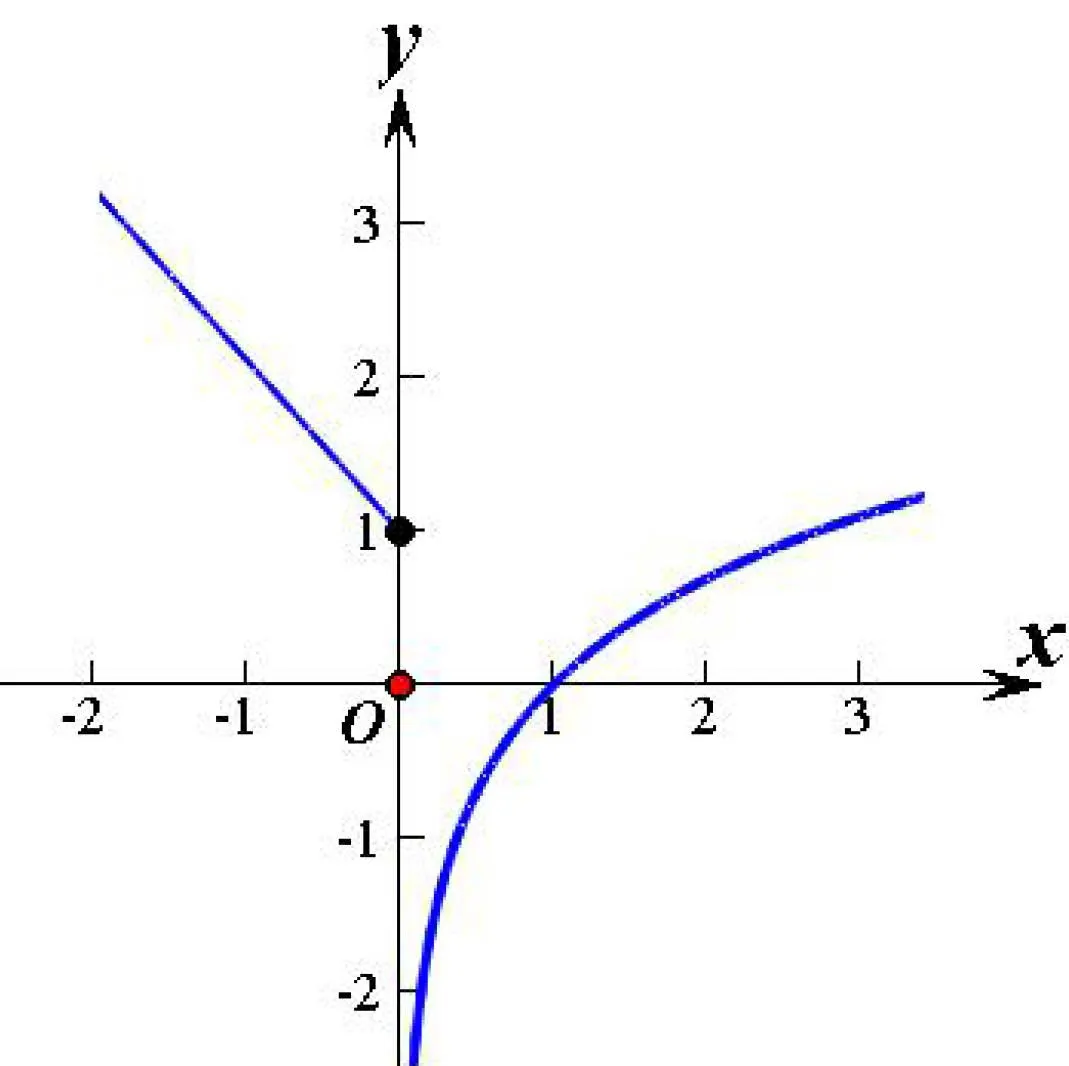
圖2

圖3

解畫出函數y=f(x)的圖像如圖所示,y=f[f(x)]+1的零點相當于求方程f[f(x)]=?1的根.當k＜0時,由f[f(x)]=?1可得f(x)≈0.5,而f(x)=0.5只有一個根.這樣就可以判斷答案為B.當k＞0時,由f[f(x)]=?1可得f(x)≈0.5或f(x)≈?1左右,而f(x)=0.5有兩個根,f(x)=?1也有兩個根,因此共有四個根.

點評本題使用了f(x)≈0.5即近似值為0.5,可以這樣做的原因是:本題只要求零點個數,不需要具體的值,采用近似值可以節約時間.

四、嘗試特殊位置 用試根法

函數零點問題是導數綜合應用的核心問題,對于一些特殊的函數,如果適當的運用試根法,可以取得化腐朽為神奇的效果.

例7(根據2011年浙江卷理科 22題改編)設函數如果對于任意的x∈(1,3],都有f(x)≥?2e成立,則a的取值范圍是( )

A.(?∞,3e]B.(?∞,1) C.[3e,+∞) D.(1,+∞)

分析要求a的取值范圍,可以先使用分離變量,然后求最值的思想.

取(1,3e]中的x,使式子可以求值,自然想到x=e,代入發現果然是g′(x)=0的根.又因為函數在(1,3e]上為增函數,所以g′(x)=0有且只有x=e這個根,而x∈(1,e)時,g′(x)＜0,x∈(e,3e)時,g′(x)＞0.因此g(x)min=g(x)=3e,可知選A.

點評試根時如果是多項式函數,常用的是0,±1,±2等等,如果含有式子lnx,則常用的是等等.

綜上所述,對于函數選擇壓軸題可以采用特殊值法、排除法、數形結合法等方法簡便巧妙的選出答案;可能有部分同學認為,不直接做,而是使用上述這些方法感覺上好像沒有把題目做出來一樣,心里不踏實.事實上,到了高三,我們需要的是分數,高考兩個小時,時間緊迫,短短的時間內要解決完大量的試題,就必須做到分秒必爭,而直接做其實就是“小題大做”;只要能選出正確答案,沒有人關心你是直接求的,還是用其他什么方法的解出來的.在實際解題中,必須有意識的培養這些特殊思想,平時做試卷還應該多加練習,到考場時自然熟能生巧,事半功倍.