汲取真題營養 提高復習效率
——談數學復習教學中對高考真題資源的利用

□馮 寅

（浙江省湖州中學，浙江湖州 313000）

復習指導

汲取真題營養 提高復習效率
——談數學復習教學中對高考真題資源的利用

□馮 寅

（浙江省湖州中學，浙江湖州 313000）

高考試題不僅是考題，也是一種對考綱的詮釋，更是我們教學的優質素材，所以挖掘高考真題的教學價值非常重要，它可以明確復習的方向，提高復習效率.

高考真題；復習效率；整體；問題；個體

高考試題是考綱、教綱的具體體現，是由命題老師精心雕琢的作品，也是數學知識、技能的濃縮，更是展現數學方法、數學思維的舞臺.因此，充分挖掘高考題的內涵，汲取它的“營養”，將使我們的教學和復習更有針對性，效率更高.

本文將以函數為例，從整體、問題、個體三個方面，探索高考真題的“營養”究竟在何處，如何汲取它的“營養”.

一、整體歸納 探求規律

高考試題是對考試大綱的具體演繹，研究多年的高考試題，我們可以發現命題的一些特點，找到復習的方向.

函數是高中數學的重要內容，也是高考的重點，從近幾年的高考函數試題中我們發現，函數問題的重要元素是參數，主要工具是導數，所以，我們可以按參數的不同和求導的特點把函數問題分為三大類型加以研究.

（一）含參求導型

問題1 已知a∈R，函數 f(x)=x3-3x2+3ax-3a+3.

（1）求曲線y=f(x)在點(1，f(1))處的切線方程；

（2）當x∈[0，2]時，求|f(x)|的最大值.

問 題 2 已 知 a＞0，b∈R,函 數f(x)=4ax3-2bx-a+b.

（1）證明：當0≤x≤1時，

①函數 f(x)的最大值為 |2a-b|+a；

② f(x)+ |2a-b|+a≥0；

（2）若-1≤f(x)≤1對x∈[0，1]恒成立，求a+b的取值范圍.

感悟 這類問題主要是求函數最值、求參數范圍和證明不等式恒成立，它主要針對三次函數、對數函數、指數函數等，它的主要方法是利用極值點含參數的特點分類討論，利用端點函數值和極值點函數值的不確定性分類討論.

（二）含參非導型

（1）求使得等式F(x)=x2-2ax+4a-2成立的x的取值范圍；

（2）①求F(x)的最小值m(a)；

②求F(x)在區間[0，6]上的最大值M(a).

問 題 4 已 知 函 數 f(x)=x2+ax+b（a,b∈R），記M(a ,b)是 |f(x) |在區間[- 1,1]上的最大值．

（1）證明：當 |a|≥2時，M(a ,b)≥2；

（2）當a,b滿足M(a ,b)≤2時，求 |a|+ |b|的最大值.

感悟 這類問題由于涉及的函數是一次、二次和絕對值居多，所以一般不需要求導，它主要解決的是參數范圍和函數零點問題，主要通過函數圖象特點、函數性質分析來解決問題.當參數較多時，我們一般會考慮是否可以減少變量或采用線性規劃的方法解決.

（三）非參求導型

證明：

感悟 這種類型看似簡單，其實對思維的要求比較高，首先要理解所證明不等式的特點，它可以構造新的函數或把要求證明的不等式轉化為我們常見的函數最大（小）值問題來分析思考，而在求極值時往往它的極值點不易求出，需要我們通過不等式放縮來改變函數從而解決問題，它考查的是函數的本質屬性.

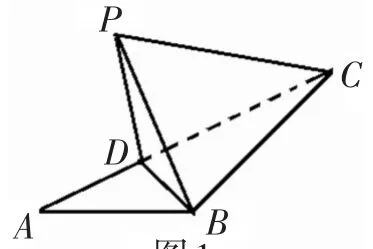
圖1

二、問題演變 借題發揮

函數的內容豐富多彩，問題形式多樣，函數最大（小）值問題是函數的重要性質，也是高考中的常見問題，但最值問題的形式和要求在不斷的演變，它對我們的思維提出了新的要求.

（一）跨越思考

問題6 如圖1，在△ABC中，AB=BC =2，∠ABC=120°.若平面ABC外的點P和線段AC上的點 D，滿足PD=DA,PB=BA，則四面體PBCD的體積的最大值是_____.

感悟 解決最值問題的起點應該是確定函數的表達式，而像此類問題的體積很難用某個變量表示，如何計算體積成為本題的關鍵，此時如果我們不跨越常規思路，問題很難解決.

設AD=x，四面體的高為h，那么h≤x.那么，四面體 PBCD的體積：VP-BCD=

此題的解法有違于我們常規的求最大值的方法，它在很難直接找到問題的表達式時，先進行了放縮，這在一般情況下是有風險的，它可能使等號無法取到，所以問題的難度就在于放縮的合理性，它需要滿足兩個要求，首先是放縮后能求出問題的表達式，然后再考慮后面的等號是否能成立，因此放縮的關鍵是找到一個合理的度滿足要求.

（二）概念理解

問 題 7 已 知 函 數 f(x)=x2+ax+b (a,b∈R)，記M(a ,b)是 |f(x) |在區間[- 1,1]上的最大值．

（1）證明：當 |a|≥2時，M(a ,b)≥2；

（2）當a,b滿足M(a ,b)≤2時，求 |a|+ |b|的最大值.

感悟 這題是近幾年考查函數最值問題的一個典型問題，它對最大（小）值概念的理解要求很高，從已知最大值到求最大值都需要深刻理解才能合理解決.

（2）中 由 M(a,b)≤2，得 |1+a+b|= |f(1)|≤2 ， |1-a+b|= |f(- 1)|≤2 ， 故|a+b|≤3 ， |a-b|≤3 ，而 得 |a|+ |b|≤

當 a=2，b=-1時， |a|+ |b|=3，且|x2+2x-1|在 [-1,1]上的最大值為2，即M(2,-1)=2.所以 |a|+ |b|的最大值為3.此題解決最值問題的方法，顛覆了傳統的求最值的思路，它省略了求函數解析式的步驟，強調了最大（小）值的概念的理解，它關注的是存在常數M，對定義域中的任意x都有 f(x)≤M成立，然后觀察等號成立.它的難點在于沒有常見的分類討論，沒有煩瑣的計算，要求對概念的深刻理解，要求有正確的思維方式.

（三）隱含挖掘

問題8 已知實數a,b,c,則（ ）.

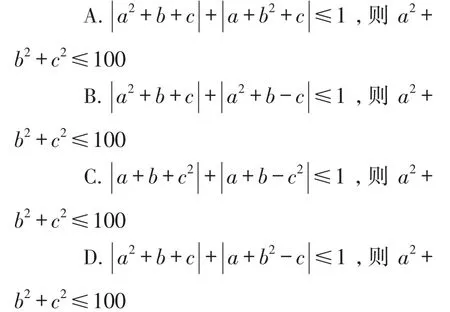
感悟 本題看似和最值毫無關系，仔細分析題意，我們從每個選擇支的結構可以看出，它的問題都是a2+b2+c2≤100，問題的核心是哪個條件能保證a2+b2+c2是有界的，有界就是最值的一種廣義表述.而要a2+b2+c2有界必須a,b,c是有界的.這樣的感悟，就將問題轉化為哪個選項中的a,b,c是有界的.

但細細體會它的核心還是和最值有關，它把最值問題擴大化，讓我們在不敘述最值的情況下感悟最值的意義和魅力，這樣的感悟對思維提出新的要求.

三、個體研究 經典深化

在近年的函數的高考題中，我們經常看到max和min這樣的符號，而簡單介紹符號的意義并不難，難的是深刻理解它們的含義，了解它們的變化，掌握它們的聯系，如果我們僅僅停留在知道符號的意思，那么當我們遇到和它們有關的問題時，還是會覺得難以適應.

（一）max和min的形式變化

問題9 已知 f(x)，g(x)都是偶函數，且在[0 ,+∞ )上 單 調 遞 增 ，設 函 數F(x)=f(x)+g(1-x)- |f(x)-g(1-x)|.若a＞0，則（ ）.

A.F(-a)≥F(a)且F(1+a)≥F(1-a)

B.F(-a)≥F(a)且F(1+a)≤F(1-a)

C.F(-a)≤F(a)且F(1+a)≥F(1-a)

D.F(-a)≤F(a)且F(1+a)≤F(1-a)

感 悟 理 解 函數 F(x)=f(x)+g(1-x) -|f(x)-g(1-x)|的表達式成為問題的關鍵，其實，為了把絕對值去掉，我們可以分類討論，這樣也可以理解為一個分段函數：

從去絕對值的分類過程，我們又可以理解為：F(x)=2min{ f(x),g(1-x)}.這樣的表達，將有助于我們解決問題.

問題的本質就轉化為比較F(a),F(-a)的大小和F(1-a),F(1+a)的大小.

很多時候max和min都直接出現在我們的問題中，但有時也會以另外的面貌出現，隱含它們的符號特征，這就需要仔細分析思考它們的含義，找出它們的表示特征來解決問題.

（二）max和min的應用策略

問題10已知a＞0，b∈R.函數f(x)=4ax3-2bx-a+b.證明：當0≤x≤1時,函數 f(x)的最大值為 |2a-b|+a.

感悟 解決函數在閉區間上的最值問題，關鍵是比較區間內極值點和端點的函數值的大小.

對函數 f(x)=4ax3-2bx-a+b求導得f'(x)=12ax2-2b.

（1）當b≤0時，f'(x)=12ax2-2b＞0，在區間[0 ,1]上 f/(x)＞0恒成立，故函數 f(x)在[0,1]上單調遞增.

所以當x∈[0 ,1]時,fmax(x)=f(1)=3a-b= |2a-b|+a；

從上述的問題我們發現，max{a ,b}和min{a ,b}有如下重要的等價變形.

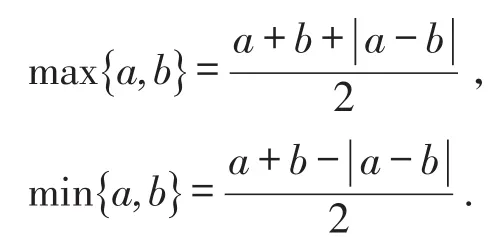
這樣的變形把分段函數和含絕對值的函數有機地整合在一起，不同形式的轉換為我們解決問題開拓了新思路.

高考試題蘊含著豐富的“營養”，是我們教學中的優質素材，挖掘高考試題的深刻內涵并滲透在我們的教學中，將使高考試題發揮它最大的價值.