不容忽視的基本概念—單位向量
上海市松江一中(201600)
董頂國●
?
不容忽視的基本概念—單位向量
上海市松江一中(201600)
董頂國●

一、運用單位向量性質破解與角平分線相關問題
單位向量如下性質:對于兩不平行的向量,其單位向量的和向量與兩個向量夾角相等.較為典型的是對三角形內心性質的證明.









說明 妙用單位向量的性質,避繁就簡,一氣呵成.
上述問題亦可拓展為一般:




類似的問題在近幾年高考中也時常出現.

A.外心 B.內心 C.重心 D.垂心
則△ABC為( ).
A.三邊均不相等的三角形 B.直角三角形
C.等腰非等邊三角形 D.等邊三角形

點評 兩個單位向量和的形式往往與三角形中角平分線密切關聯,通過聯系構造,問題變得簡單明了,是解題的有效途徑.
二、簡捷求垂線段的長度



即Ax1+By1+C=0.點P到直線的距離即為
類似的,也可導出其它相關距離問題.

再如例3.O為等邊三角形ABC內任意一點,從O點分別向BC、CA、AB作垂線,垂足分別為D、E、F,求證AF+BD+CE為定值.

AF+BD+CE

三、簡化使用向量的夾角公式
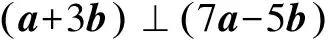


例5 如果四邊形ABCD的對角互補,且AB與CD交角的平分線為l1,AD與BC交角的平分線為l2,求證l1⊥l2.
分析 本題從題設與求證看,只與角有關,而與線段的長度無關,故可考慮通過單位向量的運算求解.

∴cos∠DCB+cos∠DAB=0.∵cos∠DCB=-e1·e4,cos∠DAB=-e3·e2,
∴e1·e4+e3·e2=0,同理e1·e3+e2·e4=0.

∴l1⊥l2.
四、簡捷證明教材中的若干定理
華師大版教材在向量運用一節,構造單位向量對兩角和的余弦公式進行過證明.實質上不少的定理也可運用單位向量給出簡潔證明.
例6 證明正弦定理及射影定理.







即c=acosB+bcosA.同理a=bcosC+ccosB,b=acosC+ccosA.
∴射影定理得證.
單位向量在數學中的應用廣泛,除以上應用外,還常構造單位向量解決三角求值,探求函數的最值及值域等問題,其特點是方法新穎、運算簡捷.總之,向量是“數”與“形”的最佳載體,而適當挖掘單位向量的潛在功能,無論對解題還是對教材的處理都大有裨益.
[1]劉紅雷.單位向量的應用例說[J].新課程,2010(5):50.
[2]毛慶華.例談單位向量的一張亮麗“名片”[J].上海中學數學,2011(11):28.
G632
B
1008-0333(2017)13-0014-02

