組件匹配與融合的三維形狀建模研究

白 茂 東， 華 順 剛， 蘇 鐵 明

( 大連理工大學 機械工程學院, 遼寧 大連 116024 )

組件匹配與融合的三維形狀建模研究

白 茂 東， 華 順 剛*， 蘇 鐵 明

( 大連理工大學 機械工程學院, 遼寧 大連 116024 )

提出一種基于組件匹配、融合的三維形狀生成算法.根據Hausdorff距離對輸入形狀的各組件進行匹配，形成匹配組件對，進行球面參數化映射，合并組件對的球面網格模型；通過反映射建立組件間的頂點對應關系，采用不同的融合系數進行插值融合，生成一系列連續變化的組件；最后根據輸入形狀的連接關系進行重新連接，生成完整的變形形狀．實驗表明，采用所提算法可以生成合理、相似的變形形狀，同時保留了輸入形狀的功能和表面細節．

組件匹配；球面參數化；網格融合；重連接

0 引 言

基于實例的三維形狀建模技術通過對已有形狀的編輯修改生成新的、功能相似的三維形狀，該技術可廣泛應用于CAD、工業造型設計、創新設計以及計算機動畫和虛擬現實等領域[1-2]，近年來已成為計算機圖形學界的研究熱點．

目前已有多種三維形狀變形生成算法涌現，其中具有代表性的方法是對現有形狀的組件進行替換、重組得到具有創意的三維形狀[3]，這類方法包括：基于形狀的約束推導分析生成新形狀[4]、根據樣式轉移方法生成融合形狀[5]、利用概率形狀結構指導組件的替換或重組[6]，以及基于集合演變方法進行三維形狀的生成[7]等．該類方法依賴輸入形狀結構，當替換含有不兼容的組件結構時，會導致不合理的結果．另一類方法通過拓撲變換、融合及重建來生成具有新的拓撲結構的三維形狀[8]．這類方法可以生成拓撲結構不同的形狀，但因需泊松重建，所以難以保證形狀的細節；且在變形過程中因拓撲發生了改變，會生成較多不合理的新形狀，需進行人工干預排除．此外，Kanai等[9]提出了一種針對等拓撲genus-0模型的變形框架，這種變形方法需要模型特征的嚴格對齊．

本文提出一種基于實例的三維網格形狀變形生成算法．三維網格形狀由點、線和面片組成，通過組件匹配、融合、重連接生成新的連續變化的形狀，這里的組件是在預處理過程中形成且具有模型部分功能意義的封閉網格．算法輸入的是經規則化及組件分割等預處理后的形狀，算法步驟綜述如下：首先，基于Hausdorff距離[10]進行輸入形狀中各組件的匹配，形成匹配組件對；其次，對各組件進行球面參數化映射，合并兩組件的球面網格模型，該模型中包括兩個輸入組件的所有頂點，通過反映射使組件對間建立頂點對應關系，進行插值融合；最后，根據輸入形狀的接觸及連接關系信息，進行重連接生成完整的變形形狀．其中插值融合形成新的網格模型包含組件的表面細節特征，采用不同的融合系數，可產生一系列連續變化的形狀．

1 組件匹配

根據設計者意圖選取兩個三維形狀作為輸入，其中一個作為原始形狀，另一個作為參考形狀，為便于組件的匹配和融合，需要對輸入的形狀進行預處理操作，包括形狀規則化、方向歸一化以及組件分割等．通過調整參考形狀頂點可以對形狀的外形尺寸進行規則化處理，根據主成分分析法[11]可以對模型方向進行歸一化．此外，許多現有算法[3，12]可以對形狀進行組件分割，使所輸入形狀由若干組件組成．由于本文所述重點是組件的匹配和融合，在此，對預處理操作不做詳細敘述．

組件匹配的目的是建立兩個給定形狀所有組件之間最佳的對應關系．對于來源于不同形狀的兩組件，可以計算它們點云數據之間的Hausdorff距離來測量組件距離．

Hausdorff距離表示的是一個度量空間內兩個非空子集之間的相互距離．它可以反映兩個集合之間的差距，因此，用它表示兩個組件之間的不相似度．

對于一個度量空間內的兩個非空集合X={x1，x2，…，xm}和Y={y1，y2，…，yn}，X到Y的Hausdorff距離定義為

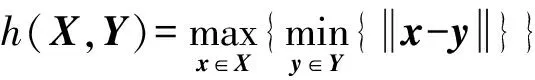
(1)

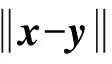
H(X，Y)=max {h(X，Y)，h(Y，X)}

(2)

該式反映了兩個集合之間的相似程度[13-14]．

組件距離為通過式(2)計算的組件網格點云數據之間的Hausdorff距離．

本文使用一種貪婪算法對兩個形狀中的組件進行匹配．其具體過程如下：首先，對于原始形狀中的每一個組件，它到參考形狀中每個組件的距離，可以通過式(2)計算，并保存在距離集H中；其次，找出其最小的Hausdorff距離Hmin，如果Hmin小于相似度閾值θ，那么與Hmin距離對應的兩個組件被認為是匹配的并作為一個匹配組件對；然后，刪除集合H中與此匹配組件對相關的其他元素，重復這一過程直到出現Hmin大于相似度閾值θ或者一個形狀中的所有組件都完成配對，如果仍存在不可匹配的組件，則被視為沒有對應關系．圖1列舉了兩個形狀匹配的一些具體實例，其中匹配的組件對用相同的顏色表示，無匹配關系的組件用淺棕色表示．

圖1 兩個形狀的組件匹配

2 基于球面參數化的組件融合

為充分保持組件表面特征，對于匹配組件對，采用基于組件融合的球面參數化[15]方法進行融合．該方法分為以下3步：第1步對匹配組件對的方向和大小進行標準化；第2步將匹配的組件分別參數化到一個單位球面上生成拓撲球Mo和Mr，并融合生成新的拓撲球Mc；第3步利用Mc頂點對匹配組件對進行反映射，獲得頂點對應關系，并進行頂點插值生成新的融合組件．

2.1 組件標準化

組件標準化的實質是對匹配組件對的頂點集Vo和Vr進行標準化．首先使用主成分分析法(principal component analysis，PCA)[11,16]對組件點云信息進行分析，然后計算出組件3個主成分，確定組件的主軸．

通常把組件的第一主成分作為主軸，但對于不同的組件，其參考組件的第一主成分可能會存在很大差異，因此，將原始組件的第一主成分作為主軸，對于參考組件，將最接近原始組件主軸的主成分作為匹配組件的主軸．如圖2所示，原始組件的第一主成分e1作為主軸eorig．顯然，對于參考組件，其第一主成分e′1與e1(即eorig)存在很大差異，因此，將最接近eorig的主成分e′2作為參考組件的主軸eref．

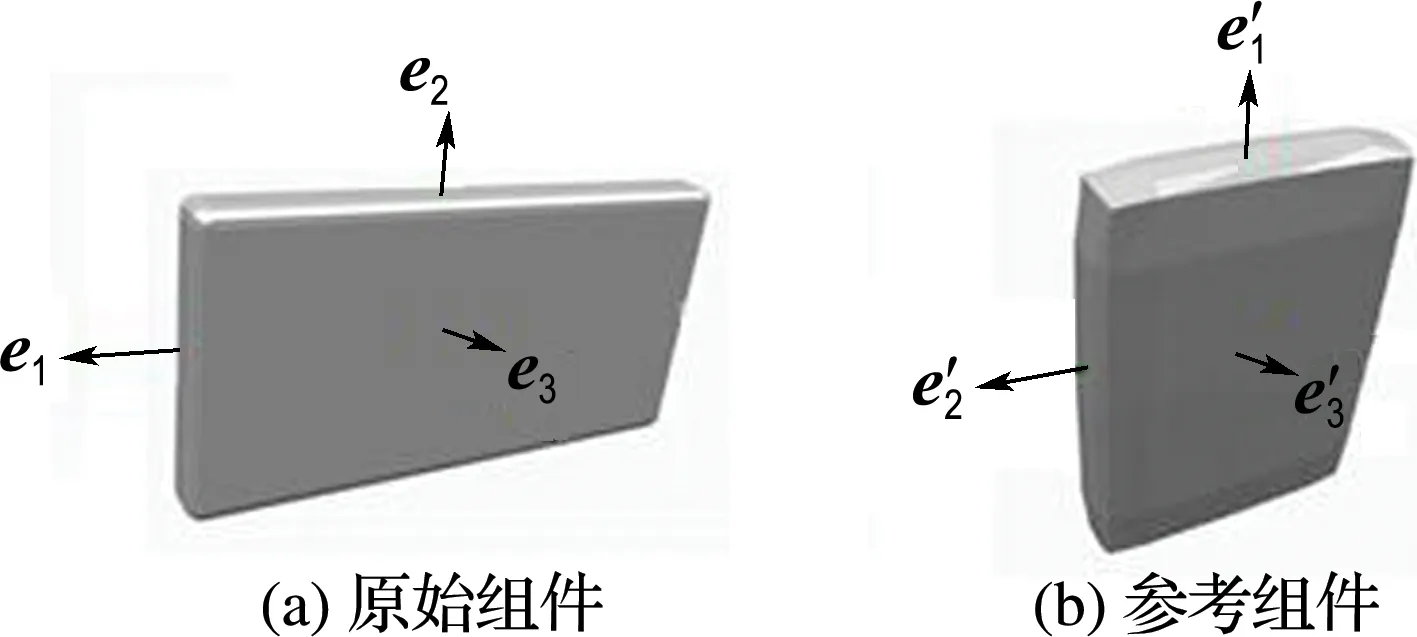
圖2 原始和參考組件的主軸選擇

接著將匹配組件對的主軸eorig和eref進行對齊．在由eorig和eref確定的平面中，通過旋轉向量eorig，使之與向量eref一致，在三維坐標系中，可以通過旋轉矩陣M實現向量的旋轉：

(3)

由此可以得到旋轉矩陣

(4)

同時得到主軸規范后原始組件和參考組件的頂點集V′o(V′o=VoM)和V′r(V′r=Vr)．為了將參考組件轉變成與原始組件具有相同包圍盒大小的結構，利用一個3×3對角矩陣S，S=diag{sx，sy，sz}，對組件進行縮放，其中sx、sy和sz分別為原始組件和參考組件的包圍盒3個主軸方向邊的長度比．

2.2 球面參數化

組件標準化后，根據球面中心投影法將組件映射到一個單位球上，組件的質心即為球心．為了消除映射產生的疊影，本文使用拉普拉斯迭代方法[17]進行過濾．拉普拉斯算子通常被定義為一種低通濾波器，它可以過濾高頻，而疊影常發生在球體表面頂點的高頻區域，所以使用拉普拉斯迭代來消除疊影．其數學表達式為

(5)

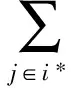
V′=V+ΔV={v′i|v′i=vi+Δvi，Δvi=L(vi)}

(6)

迭代的過程即為消除疊影的過程，迭代完成后，即可得到原始組件和參考組件的球面參數化網格模型Mo和Mr．

接下來對網格模型Mo和Mr進行拓撲融合生成拓撲球Mc，拓撲球Mc包含Mo和Mr中所有頂點及網格相交生成的交點．如圖3所示，實心點屬于參數化到Mo上的頂點，空心點屬于參數化到Mr上的頂點．在Mo和Mr的網格模型上，其任意一條邊與球心O的連線可以形成新的面，在Mc中當兩者相交時會產生一條通過球心的直線(如圖3中的紅線所示)，該直線與單位球表面的交點，即為新生成的點．然后遍歷每一條邊，并按照順時針方向進行邊循環創建面，如圖4所示，新形成的面可能含有3條邊、4條邊等，最后基于銳角三角形原則進行三角化形成最終的網格模型Mc．

圖3 Mo和Mr之間的交點

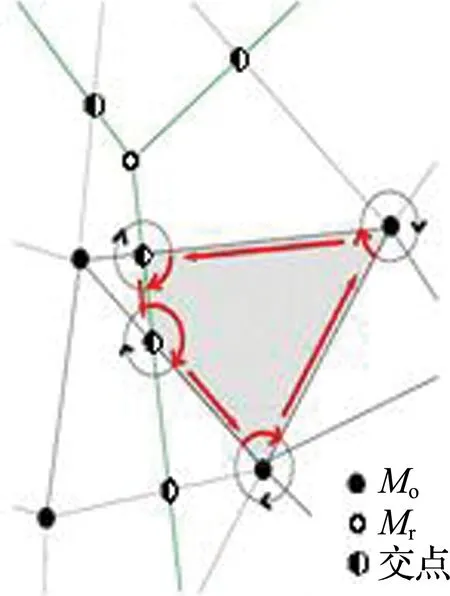
圖4 在Mc中沿著邊循環創建面

2.3 反映射與組件生成

融合生成的網格模型Mc包含了原始組件和參考組件的所有頂點信息，反映射的過程實際就是利用Mc的頂點坐標分別表示原始組件及參考組件頂點的過程．根據上述Mc的頂點分類，反映射過程中，它的每一個頂點都必須被考慮和確定，這里用計算反映射原始組件Vc-o的變換進行說明．對于Mo的每一個頂點，它必須被包含在Mc上一個確定的三角形面片中，考慮到三角形頂點的相對位置，利用Mc包含的三角形去計算Mo的頂點，并用Mc上的頂點坐標進行表示．這樣Mo的頂點就得到了重新計算，也就完成了Vc-o的變換．同理可得到反映射參考組件的Vc-r的變換，具體的組件融合與反映射過程如圖5所示．

如上所述，利用Mc的網格結構表示原始組件以及參考組件的變換，即Vc-o和Vc-r，可以獲取原始組件及參考組件上所有頂點的對應關系．如圖6所示，通過在Vc-o和Vc-r進行頂點插值，生成組件由原始組件向參考組件進行轉變．融合頂點可以計算如下：

Vc(k)=kVc-o+(1-k)Vc-r

(7)

其中k(0

圖5 組件球面參數化、網格融合及重建過程

圖6 組件融合

3 組件重連接

(a) 融合后的組件分離現象

(b) 重連接后的合理形狀

圖7 組件重連接

Fig.7 Component relinking

雖然組件融合保留了原始頂點的拓撲關系，但融合生成的組件在幾何形狀、維度以及位置上會產生變化．如果直接將生成的組件進行連接，則可能會發生如圖7(a)所示的組件分離等現象．為確保連接和拓撲變化的合理性，本文選擇幾何尺寸最大或者位于原始形狀正中心的組件作為基礎組件，然后獲取相對于該組件其他所有組件的位置，從而進行組件重連接．如果原始形狀的兩個組件具有連接關系c1=(S1，S2)，S1和S2是通過兩個組件最近的頂點集，那么，可以類似地獲得它們在參考形狀中分別匹配的組件對應的連接關系c2=(S′1，S′2)．對于融合系數k，融合后的組件對應連接關系cb(k)可以通過公式cb(k)=kc1+(1-k)c2計算得到．如圖7(b)所示，按照其計算后的連接關系調整融合后的組件，將形成完整合理的形狀．

4 實驗驗證

在Intel i5處理器、3.30 GHz主頻、 8 GB內存臺式機上對本文算法進行實驗驗證，使用C++ 語言在VS2010開發平臺對off網格模型進行處理．為驗證本文算法的有效性和實用性，從互聯網和一些文獻中[8，18]收集若干三維網格模型，如桌子、椅子、飛機等，實驗結果如圖8所示．

每一行從左到右融合系數k依次取值為0、0.2、0.4、0.6、0.8、1.0．對于輸入形狀，如果所有組件都具有一對一匹配關系，那么無論選擇誰作為原始組件，其變形結果都相同；對于沒有匹配關系的組件，只作簡單保留．相較于組件替換及拓撲變化的形狀生成方法[8]，本文算法能夠生成合理的表面變形，同時保留輸入模型功能合理性和表面細節．在圖8中，每行模型都能基于輸入產生完整的過渡變化效果且保持了輸入的功能合理性，第1、2和4行原始桌腿的表面紋理在變化中被很好地繼承下來，第9和10行娃娃頭部特征也被很好地繼承下來．

圖8 形狀生成實例

根據輸入形狀的多樣性，雖然所提出的算法可以生成大量的變形形狀，但每一個三角形面片和頂點都將基于輸入的網格模型被計算處理成新的網格，因此，需要輸入具有良好網格結構的形狀模型．

5 結 語

基于組件匹配和融合，實現了三維形狀的生成．算法首先基于Hausdorff距離對輸入形狀的組件進行匹配，獲得匹配組件對；為避免表面凹凸遮擋現象，解決頂點對應的準確性，便于獲得形狀表面細節，將匹配組件對球面參數化，融合生成新的包含兩組件全部頂點的網格模型；然后用融合的網格對組件進行反映射計算，新生成的網格模型包含輸入組件的所有頂點對應關系．頂點插值時根據融合系數的不同取值，獲得不同的組件形狀；最后基于輸入形狀的連接關系將生成的組件進行重連接，產生連續變化的形狀．本文提出的匹配融合算法生成的形狀具有合理的幾何外觀和功能，并保留了輸入形狀的細節．

[1] WATSON I, PERERA S. Case-based design: A review and analysis of building design applications [J]. Artificial Intelligence for Engineering Design Analysis and Manufacturing, 1997, 11(1):59-87.

[2] LIU Qiaosheng, XI Juntong. Case-based parametric design system for test turntable [J]. Expert Systems with Applications, 2011, 38(6):6508-6516.

[3] KALOGERAKIS E, CHAUDHURI S, KOLLER D A. A probabilistic model for component-based shape synthesis [J]. ACM Transactions on Graphics, 2012, 31(4):55.

[4] JAIN A, THORMHLEN T, RITSCHEL T,etal. Exploring shape variations by 3D-model decomposition and part-based recombination [J]. Computer Graphics Forum, 2012, 31(2):631-640.

[5] HAN Zhizhong, LIU Zhenbao, HAN Junwei,etal. 3D shape creation by style transfer [J]. The Visual Computer, 2015, 31(9):1147-1161.

[6] CHAUDHURI S, KALOGERAKIS E, GUIBAS L,etal. Probabilistic reasoning for assembly-based 3D modeling [J]. ACM Transactions on Graphics, 2011, 30(4):35.

[7] XU Kai, ZHANG Hao, COHEN-OR D,etal. Fit and diverse:Set evolution for inspiring 3D shape galleries [J]. ACM Transactions on Graphics, 2012, 31(4):57.

[8] ALHASHIM I, LI Honghua, XU Kai,etal. Topology-varying 3D shape creation via structural blending [J]. ACM Transactions on Graphics, 2014, 33(4):158.

[9] KANAI T, SUZUKI H, KIMURA F. Metamorphosis of arbitrary triangular meshes [J]. IEEE Computer Graphics and Applications, 2000, 20(2):62-75.

[10] Wikipedia. Hausdorff distance [Z/OL]. [2016-07-28]. https://en.wikipedia.org/wiki/Hausdorff_distance.

[11] ABDI H, WILLIAMS L J. Principal component analysis [J]. Wiley Interdisciplinary Reviews:Computational Statistics, 2010, 2(4):433-459.

[12] SHAMIR A. A survey on mesh segmentation techniques [J]. Computer Graphics Forum, 2008, 27(6):1539-1556.

[13] ROTE G. Computing the minimum Hausdorff distance between 2 point sets on a line under translation [J]. Information Processing Letters, 1991, 38(3):123-127.

[14] RUCKLIDGE W. Efficient computation of the minimum Hausdorff distance for visual recognition [D]. Ithaca:Cornell University, 1995.

[15] ALEXA M. Recent advances in mesh morphing [J]. Computer Graphics Forum, 2002, 21(2):173-196.

[16] PAPADAKIS P, PRATIKAKIS I, PERANTONIS S,etal. Efficient 3D shape matching and retrieval using a concrete radialized spherical projection representation [J]. Pattern Recognition, 2007, 40(9):2437-2452.

[17] TAUBIN G. Signal processing approach to fair surface design [C] // Proceedings of the ACM SIGGRAPH Conference on Computer Graphics. New York: ACM, 1995:351-358.

[18] ALHASHIM I, XU Kai, ZHUANG Yixin,etal. Deformation-driven topology-varying 3D shape correspondence [J]. ACM Transactions on Graphics, 2015, 34(6):236.

Research on 3D shape modeling using component matching and merging

BAI Maodong, HUA Shungang*, SU Tieming

( School of Mechanical Engineering, Dalian University of Technology, Dalian 116024, China )

A 3D shape creation algorithm based on component matching and merging is proposed. Components are matched between two input shapes according to the Hausdorff distance metric to generate matched component-pairs. The components are mapped onto the spherical surface to carry out the spherical parameterization. The spherical meshes of two matched components are merged, and the vertices correspondence between matched component-pairs are built through reverse mapping.The interpolation is concluded to create a series of in-betweens in terms of the merging coefficient. Finally, the novel variations are obtained by relinking components with reference to the connection of input shapes. Experiments show that the proposed algorithm can generate reasonable and plausible variations, while retaining the function and adequate surface details of the input shapes.

components matching; spherical parameterization; mesh merging; relinking

1000-8608(2017)03-0241-06

2016-08-15；

2017-03-28．

國家自然科學基金資助項目(61300085).

白茂東(1989-)，男，博士生，E-mail:baimaodong@mail.dlut.edu.cn；華順剛*(1964-)，男，教授， E-mail:hsgang02@dlut.edu.cn；蘇鐵明(1972-)，男，講師，E-mail:tiemings@dlut.edu.cn.

TP391

A

10.7511/dllgxb201703004