投資組合優化模型的一個序列凸近似算法

李 衛 國， 張 宏 偉， 梁 錫 軍

( 1.大連理工大學 數學科學學院, 遼寧 大連 116024；2.遼寧地質工程職業學院， 遼寧 丹東 118303；3.中國石油大學(華東) 理學院， 山東 青島 266580 )

投資組合優化模型的一個序列凸近似算法

李 衛 國1,2， 張 宏 偉*1， 梁 錫 軍3

( 1.大連理工大學 數學科學學院, 遼寧 大連 116024；2.遼寧地質工程職業學院， 遼寧 丹東 118303；3.中國石油大學(華東) 理學院， 山東 青島 266580 )

以CVaR為代表的凸優化投資組合模型近年來引起了廣泛研究．為克服傳統投資組合模型中凸近似的不足，提出了一個投資組合的DC規劃模型．該模型用一個DC函數替代了CVaR模型中的凸近似函數，同時要求所有約束條件在概率意義下成立．進一步地，提出了一個序列凸近似(SCA)算法用于求解DC規劃問題，并運用Monte-Carlo方法來實現SCA算法．初步的實驗結果表明，因子收益服從“尖峰厚尾”分布時，模型的目標函數值優于采用CVaR近似的目標函數值．

投資組合；序列凸近似；凸優化；Monte-Carlo方法

0 引 言

投資組合是指投資者根據其風險喜好在眾多的有價證券中對風險投入進行最優投資分配．投資組合選擇問題最早由Markowitz[1]作為一個最優化問題提出．他用隨機收益率的均值來衡量預期收益的好壞，用隨機收益率的方差衡量風險的大小．Markowitz的均值-方差模型在現代投資理論中堪稱經典，并且始終在改進．例如文獻[2]對這些模型作了一個系統的總結．只有當證券收益率服從正態分布或者投資者是風險厭惡型時，均值-方差模型才是有效的．但由于計算的復雜性，在投資數額較大的優化問題中模型的使用率并不高．本文試圖改進這一模型，研究不同的預期收益或風險衡量標準，使得模型更符合實際，更好地為投資者決策提供參考．

投資者經常會遇到投資項目的組合決策問題，要考慮的因素有收益率、風險、增長潛力等條件，希望該資產投資波動越小越好，并進行權衡考慮獲得一個最佳的投資方案．在投資組合的優化研究過程中，本文試圖在傳統的保守近似優化模型的基礎上，克服指示函數I(0，+∞)(z)在近似估計中的不足．通過引入風險度量的DC(difference of two convex functions)近似，給出一個投資組合的DC規劃模型，并提出一個序列凸近似(sequential convex approximation，SCA)算法來進行求解，用一個嚴格凸二次函數來近似目標函數中的光滑函數，用線性函數近似所有DC函數的第二個凸函數，得到搜索方向的一系列的凸優化問題．

1 問題提出

r=μ+VTξ+ε

maxE[rTx]=μTx+xTVTEF(ξ)

其約束條件被稱為決策風險[3]，用

來描述，其中1=(1 1 … 1)T∈Rn，β∈(0，1)是一個較小的數，a>0是保守收益的一個估計．同時希望該資產的投資波動越小越好．采用var(rTx)=xTDx，作為投資波動的度量．考慮如下模型：

maxE[rTx]=μTx+xTVTEF(ξ)-γxTDxs. t.Prob{-(μTx+xTVTξ)≤-a}≥1-β1Tx=1，x≥0

(1)

其中γ>0是參數．考慮模型(1)中的概率約束，令

p(x)=1-Prob{-(μTx+xTVTξ)+a≤0}=Prob{-(μTx+xTVTξ)+a≥0}

則約束條件

1-p(x)≥1-β?p(x)≤β

p(x)=Prob{c(x，ξ)>0}=E[I(0，+∞)(c(x，ξ))]

其中

c(x，ξ)∶=μTx+xTVξ-a

這里IA(·)表示集合A上的指示函數：

在Rockafellar等[4]提出的CVaR近似中，用

ψ(z，t)=[t+z]+/t

近似I(0，+∞)(z)，其中z>0，[z]+=max{z，0}．

Nemirovski等[5]曾經指出在所有的凸的保守近似中，CVaR被公認為是最出色的．但是，ψ(z，t) 對于指示函數I(0，+∞)(z)不是一個好的近似，因為在z>0且z較大時，兩個函數差異較大．為尋求一個更好的近似，令

由于ψ(z，t)和φ(z，t)都是z的凸函數，π(z，t)是一個關于z的DC函數．函數π(z，t)僅在區間(-t，0)與指示函數有差異，在其余的區間與指示函數完全吻合．可見，DC函數π(z，t)是指示函數的一個更好的近似，如圖1所示．

令

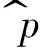
p＾

(

x

，

t

)=

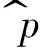
p＾

(

x

，

t

)是

p

(

x

)的一個保守DC近似．

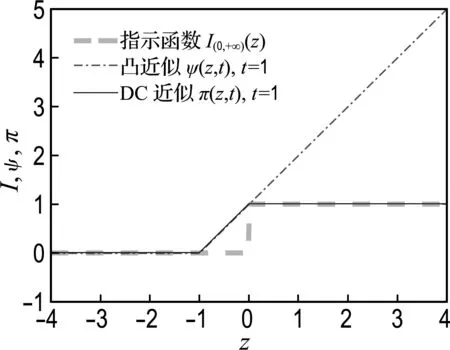
圖1 DC近似與凸近似

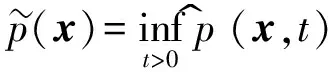
p (x)=inft>0p＾(x，t)

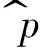
p＾

(

x

，

t

)≤

β

?

因此，

是

p＾

(

x

，

t

)所有近似中最好的保守近似．

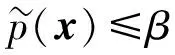
1Tx=1，x≥0

(2)

稱模型(2)為模型(1)的DC近似[6]．

maxμTx+xTVTEF(ξ)-γxTDxs.t.g1(x，t)-g2(x)≤βt1Tx=1，x≥0

(3)

記Ω(t)為模型(3)的可行域：

Ω(t)∶={x∈X：g1(x，t)-g2(x)≤βt， 1Tx=1，x≥0}

算法1是求解模型(3)的序列凸近似算法．

算法1 序列凸近似(sequential convex approximation，SCA)算法

SCA算法具體步驟如下：

Step 1 選取x0∈Ω(t)，k=0．

Step 2 若xk是最優解，算法終止．

Step 3 用Monte-Carlo方法[6]求解下列凸規劃問題：

g

2

(

x

k

)，

x

-

x

k

〉]≤

βt

1

T

x

=1，

x

≥0

(4)

得最優解xk+1．

Step 4k∶=k+1，轉Step 2．

2 SCA算法的實施

2.1 凸規劃問題(4)的求解

依照前面的記號

c(x，ξ)=μTx+xTVTξ-ag1(x，t)=E[c(x，ξ)+t]+=E[I[0，+∞)(c(x，ξ)+t)]

g2(x，t)=g1(x，0)

另外，記h(x)為問題(4)的目標函數：

h(x)∶=μTx+xTVTEF(ξ)-γxTDx

則有

令

(5)

則

(6)

記ξ1，ξ2，…，ξn為隨機變量ξ的獨立同分布的樣本點．

(7)

g2(xk)=1n∑ni=1xc(xk，ξi)·I[0，+∞)(c(xk，ξi))

(8)

(9)

對g(x)的一個自然的估計是

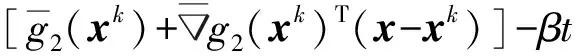
[g2(xk)+g2(xk)T(x-xk)]-βt

(10)

為了在n較大時有效地求解問題(4)，給出下面的方法：由式(5)、(6)及文獻[7]引理2知，

g

(

x

)可以近似為

g(x)=

1n∑ni=1xc(xk，ξi)·I[0，+∞)c(xk，ξi)

g

(

x

)的近似，并直接用基于梯度

[8]

的方法求解問題(4)．該方法可以視為用近似的

g

(

x

)、

g

(

x

)及

E

(

ξ

)直接求解問題(4)．當采用基于梯度的方法求解問題(4)時，樣本點僅用于計算

(

x

)和

g

(

x

)的值．所需的計算量是

O

(

n

)．這是求解問題(4)的一種較快的方法．

2.3 初始點的選取

為執行SCA算法，需要選取初始點x0∈Ω(t)，給出兩種選取辦法．

第一種，記

Ω0(t)={x∈X：g1(x，t)≤βt， 1Tx=1，x≥0}

注意到，g2(x)=E[μTx+xTVTξ-a]+≥0，?x∈X．故Ω0(t)?Ω(t)．另外，由于g1(x，t)是關于x的凸函數，故Ω0(t)是凸集合．于是，

是凸規劃．令xε=arg min{h(x)：x∈Ω0(t)}，則xε∈Ω(t)．

令t*=q1-β(c(xCVaR，ξ))，即c(xCVaR，ξ)的1-β分位數．由文獻[9]，t*>0且

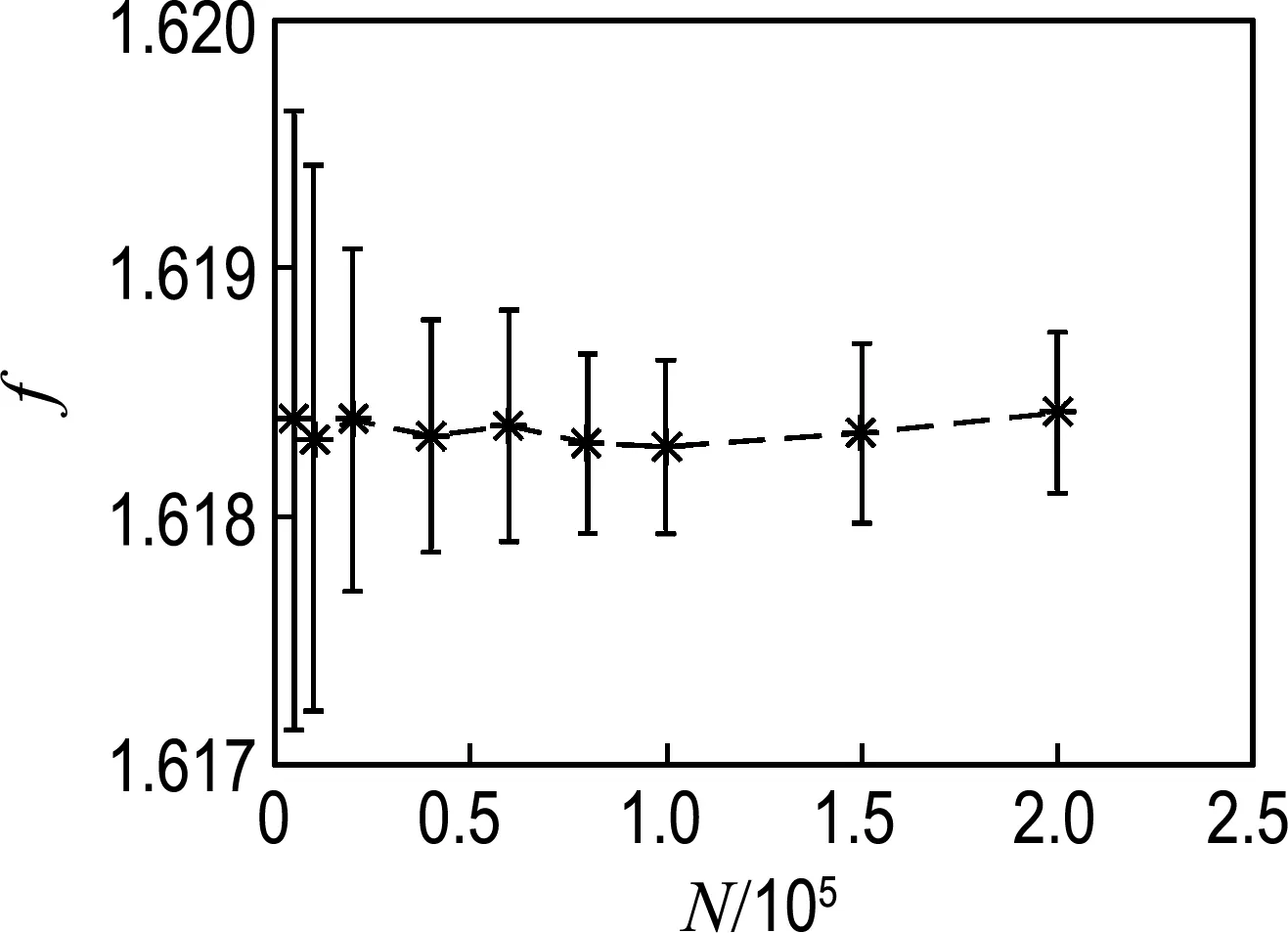
于是，xCVaR∈{x∈X：g1(x，t*)≤t*β}．由于g2(x)≥0，故xCVaR∈{x∈X：g1(x，t*)-g2(x)≤t*β}=Ω(t*)．對于任意t∈(0，t*]，Ω(t*)?Ω(t)．因此，xCVaR∈Ω(t)，0

(1)CVaR近似解的計算

xCVaR=arg min{h(x)：CVaR1-βc(x，ξ)≤0，1Tx=1，x≥0}

(11)

(2)CVaR分位數的計算

令L1，L2，…，Ln是損失L的n個獨立同分布的觀測，則L的α-VaR可以估計為

v＾nα=Lnα：n

L的α-CVaR可以估計為

c＾nα=v＾nα+1n(1-α)∑ni=1[Li-v＾nα]+

(12)

(3)CVaR分位數的梯度估計

假設隨機損失L是參數θ的函數，記為L(θ)．L(θ)關于θ可微．對任意的θ，設vα(θ)、cα(θ) 是L(θ)的α-VaR和α-CVaR，0<α<1，它們都是θ的函數．

依據文獻[10]定理3.1，在適當的條件下，對于任意的θ，

c′α(θ)=E[L′(θ)|L(θ)≥vα(θ)]

(13)

記(L1，D1)，(L2，D2)，…，(Ln，Dn)為(L(θ)，L′(θ))的n個獨立同分布的觀測．提出c′α(θ)的估計：

Γn=1n(1-α)∑nj=1Dj·1Lj≥v＾αn

3 實 驗

采用下面的數據進行測試：各資產的平均收益μ=(1.0 1.2 1.4 1.6 1.8)T，期望收益a=1.5，因子荷載矩陣

方差-協方差矩陣

實驗測試ξ=(ξ1ξ2…ξp)T服從如下兩種分布的情形．(1)ξ服從F分布：ξi～F(i+2，i+4)，i=1，2,…，p；(2)ξ服從正態分布：ξi～N(πi，ρi2)，i=1，2,…，p，為了比對兩種情形，取均值πi、方差ρi2與情形(1)中相應的F分布的均值和方差相同．

序列凸近似算法的參數設為γ=1.0，β=0.05，t=0.01．算法在Matlab 2012a平臺下編程實現，在Intel Core i7-4770 CPU 3.40 GHz，8 GB RAM計算機上執行．

-近似解和

CVaR

近似得到的解作為

SCA

算法的初始點．隨機變量

ξ

的抽樣次數為1.0×10

5

．圖2中給出了目標函數值

f

隨迭代次數

k

的變化，

ξ

分別服從

F

分布和正態分布．可以看出，無論

ξ

服從

F

分布還是正態分布，CVaR初始點處的目標函數值大于

-近似解處的目標函數值，并且在兩種不同的初始點下，目標函數值隨迭代次數的增加而增加，最終近乎收斂于共同的函數值．

ξ

服從

F

分布時(圖2(a))，算法改進了

-近似的目標函數值(1.605 6)和CVaR近似的目標函數值(1.608 0)：算法收斂時的目標函數值為1.621 2．兩種初始點計算出的最優解皆為

x

*

=(0 0 0.171 2 0 0.828 8)

T

．可見模型選擇了第3個和第5個資產進行資產配置．

ξ

服從正態分布時(圖2(b))，算法改進了

-近似的目標函數值(1.618 2)和CVaR近似的目標函數值(1.618 3)：算法收斂時的目標函數值為1.618 7．兩種初始點計算出的最優解皆為

x

*

=(0 0 0.203 8 0 0.796 2)

T

．可見模型仍選擇了第3個和第5個資產進行資產配置，但資產配置比例與

ξ

服從

F

分布時的情形有差別．

為測試抽樣規模的影響，實驗比較了不同抽樣規模下的目標函數值以及計算時間(單位：s)，如圖3所示(ξ服從F分布)．在每個抽樣規模下，進行了100次重復實驗，目標函數值和計算時間取其平均值，圖中畫出了其標準差(每個柱線段的長度是相應標準差的2倍)．由圖3(a)可以看出，目標函數值的標準差在抽樣規模N大于0.5×105時趨于穩定(標準差小于1.0×10-3)；圖3(b)顯示，計算時間隨抽樣規模的增長而增加．ξ服從正態分布時有類似的規律，見圖4．

(a) 目標函數值

(b) 計算時間

(a) 目標函數值

(b) 計算時間

4 結 語

本文考慮因子收益ξ服從“尖峰厚尾”分布的情形，例如F分布，用DC函數來近似概率約束中的指示函數，將資產投資組合問題建模為一個DC規劃，并提出了求解該DC規劃的序列凸近似(SCA)算法．該算法通過迭代求解一系列凸二次規劃問題，來計算原問題最優解．通過所提出的梯度近似計算方法，減少了算法的計算量．初步的數值實驗結果表明，所提出的模型及SCA算法是有效的．因子收益ξ服從F分布時，目標函數值優于采用CVaR近似的目標函數值．

[1] MARKOWITZ H M. Portfolio selection [J]. Journal of Finance, 1952, 7(1):77-91.

[2] MITRA G, KYRIAKIS T, LUCAS C,etal. A review of portfolio planning:models and systems [J]. Advances in Portfolio Construction and Implementation, 2003, 26(1):1-39.

[3] GOLDFARB D, IYENGAR G. Robust portfolio selection problems [J]. Mathematics of Operations Research, 2003, 28(1):1-38.

[4] ROCKAFELLAR R T, URYASEV S. Optimization of conditional value-at-risk [J]. Journal of Risk, 2000, 2(3):21-40.

[5] NEMIROVSKI A, SHAPIRO A. Convex approximations of chance constrained programms [J]. SIAM Journal on Optimization, 2006, 17(4):969-996.

[6] HONG L J, YANG Yi, ZHANG Liwei. Sequential convex approximations to joint chance constrained programms: a Monte Carlo approach [J]. Operations Research, 2011, 59(3):617-630.

[7] GLASSERMAN P. Monte Carlo Methods in Financial Engineering [M]. New York: Springer, 2004.

[8] FREUND R M. Subgradient optimization, generalized programming, and nonconvex duality [R]. Cambridge: Massachusetts Institute of Technology, 2004.

[9] PFLUG G C. Some remarks on the value-at-risk and the conditional value-at-risk [M] // Probabilistic Constrained Optimization: Methodology and Applications. New York: Springer US, 2000:272-281.

[10] HONG L J, LIU Guangwu. Simulating sensitivities of conditional value-at-risk [J]. Management Science, 2009, 55(2):281-293.

A sequential convex approximation algorithm for portfolio optimization model

LI Weiguo1,2, ZHANG Hongwei*1, LIANG Xijun3

( 1.School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China；2.Liaoning Geology Engineering Vocational College, Dandong 118303, China；3.College of Science, China University of Petroleum, Qingdao 266580, China )

CVaR has drawn extensive attentions as a representative convex optimization portfolio model in recent years. To overcome the limits of convex approximations in traditional portfolio models, a DC programming model for portfolio is proposed. In the proposed programming model, a DC function is used as a surrogate for the convex approximation function in the CVaR model. All the constraints are satisfied in the probabilistic sense in the DC programming problem. Moreover, a sequential convex approximation (SCA) algorithm is designed to solve the DC programming problem. The SCA algorithm is implemented by employing Monte-Carlo method. Preliminary experimental results have shown that the objective function values of the DC programming are better than those with CVaR approximation when the income factors satisfy ″high peak and fat tail″ distributions.

portfolio; sequential convex approximation; convex optimization; Monte-Carlo method

1000-8608(2017)03-0321-06

2016-08-20；

2017-03-25．

國家自然科學基金資助項目(61503412)；遼寧省教育科學“十三五”規劃研究項目(JG16EB101).

李衛國(1974-)，男，博士生，E-mail:liguoguo1@sina.com.cn；張宏偉*(1955-)，男，教授，E-mail:hwzhang@dlut.edu.cn.

O224

A

10.7511/dllgxb201703016