操作變量與前饋變量轉換對模型預測控制可行域影響機制

羅 雄 麟， 張 佳， 許 鋒， 許 鋆

( 中國石油大學 自動化系， 北京 102249 )

操作變量與前饋變量轉換對模型預測控制可行域影響機制

羅 雄 麟*， 張 佳， 許 鋒， 許 鋆

( 中國石油大學 自動化系， 北京 102249 )

模型預測控制因其解耦性和強魯棒性得以在過程控制中廣泛使用．在實際生產過程中，因操作需要常常放開控制器對部分操作變量的控制，此部分操作變量則轉化為前饋變量．變量之間的轉換將使系統的結構在方系統、胖系統和瘦系統之間發生轉換．對于瘦系統，操作變量的維數少于被控變量，其控制效果往往低于其他結構的系統．同時，原操作變量不被控制器控制后，轉換為前饋變量，也會影響對系統的控制效果．可行域能直接反映系統控制效果．在對狀態空間模型進行多步預測推導的基礎上，將部分控制變量與前饋變量進行轉換，用空間幾何映射表示變量轉換，并分析轉換對系統可行域的影響．最后，針對實際生產過程中放開部分控制變量的情況，提出預判機制，以保證系統可控．

過程控制；模型預測控制；前饋變量；可行域

0 引 言

模型預測控制由于其良好的約束處理能力、解耦性和強魯棒性，在復雜工業系統中展現了良好的控制性能，在工業過程中應用廣泛[1-5]．經過30多年的研究，模型預測控制已取得重大發展．

在預測控制系統穩定性的研究方面，近年來成果頗豐[6-7]．此類研究中，常常將系統分為方系統和非方系統，非方系統又可分為胖系統和瘦系統[8]．方系統和胖系統由于操作變量的維數等于或多于被控變量的維數，其控制方法和控制穩定性往往都要優于瘦系統．實際的化工過程系統維數都比較高，由于約束的作用，很多操作變量無法在控制過程中發揮作用[9]，系統結構常常在方系統、胖系統和瘦系統之間轉換．系統結構的轉換對于系統的穩定性甚至可控性有非常大的影響．大多數系統的操作變量與被控變量之間并不是一一對應的，這為此類系統的研究增加了難度[10]．

在生產過程中，由于實際控制的需要，常常放開控制器對部分操作變量的控制，此部分操作變量轉換為系統的干擾變量．由于操作變量的減少，系統結構變化會給系統的穩定性和可控性帶來影響．同時，由于干擾變量的增加，系統穩定性也會發生改變．

近年來，學者們對于系統的研究均是基于系統結構不會發生變化的前提下進行的，但是實際生產過程中，系統結構常會因各種外界因素的影響發生變化．系統結構發生變化后，對系統的所有優化都不再能實現期望的控制效果．可見，系統結構變化對系統控制效果的影響機制研究是非常有意義的．

預測控制研究中，對于擾動變量的處理目前主要有兩種方法[11-14]，應用最廣泛的是通過加入干擾觀測器來抑制擾動的作用，其次是通過辨識或物理建模獲得干擾的模型并采用前饋的方法加以抑制．以上方法的缺點就是不能直觀地分析擾動對控制效果的影響．而且，現有對擾動的研究局限于外部擾動[15]，并未考慮系統操作變量的轉換產生的擾動對系統的影響．

可行域作為預測控制系統穩定性和可控性研究的重要參數[16]，在優化系統控制算法、預測約束可行性分析方面起著至關重要的作用，其大小直接由系統變量的約束范圍確定．當外力因素使得系統的變量之間發生轉換時，必然會引起系統可行域的變化．

針對約束預測控制中可行域變化問題，Graichen等[17]提出將帶有約束的變量，通過變換得到與原始預測控制表達式類似的不考慮約束的表示形式，該方法有效避免操作變量達到約束飽和而成為系統擾動，但針對主動使預測控制器釋放部分操作變量(變為擾動變量)、系統可行域發生變化的情況并未給出說明．其后，大多數學者都遵循此思路，以避免控制變量維數降低使可行域變化而帶來的影響．

針對控制變量維數減少的情況，杜曉寧[18]和李德偉等[19]提出了減少預測控制器控制變量維數的算法，以降低預測控制滾動優化計算量，此算法專注于對被控變量進行抽象計算，并未考慮減少控制變量個數這一策略對系統穩定性的影響，缺少理論指導機制．

由此可見，目前針對由于變量達到約束飽和或人為主觀因素調控使得控制變量維數減少且轉換為前饋擾動的問題，還沒有進行過多研究．而此研究對實際工業過程中頻繁的變量轉換現象，具有很重要的理論指導意義．

沿此思路，本課題組針對引入前饋變量的情況下預測控制可行域的變化問題，已進行了相關研究分析．通過映射的直觀手段，使用凸空間[20]的思想，求得可行域的頂點集合，進而求解得出引入前饋變量對可行域大小的影響[21]．

在上述研究基礎上，本文將利用映射的思想[22]，在對狀態空間模型進行P步預測推導的基礎上，將部分控制變量與前饋變量進行轉換，分析可行域映射空間交集的變化，針對實際生產過程中需要放開部分控制變量的情況，研究變量轉換對預測系統可行域的影響機制．

1 預測控制操作變量與前饋變量的轉換

1.1 MIMO系統狀態空間模型描述

模型預測控制的系統狀態空間模型如下[23]：

x＾(k+1k)=Ax＾(kk)+Bu(k)y＾(kk)=Cx＾(kk)

(1)

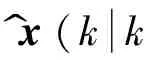
x＾(kk

y＾(kk)=y(k)

式中)∈Rn表示k時刻對k+i時刻系統中間狀態的估計，)=x(k)表示系統當前時刻的已知狀態；u(k)∈Rm表示操作變量；y(k)∈Rr表示被控變量，表示系統當前時刻的輸出．系數矩陣A∈Rn×n,B∈Rn×m,C∈Rr×n．

對輸出的P步預測為

x＾(k+1k)=Ax(k)+Bu(k)

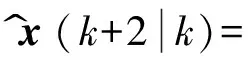
x＾(k+2k)=

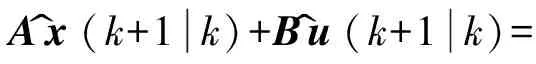
Ax＾(k+1k)+Bu＾(k+1k)=

A2x(k)+ABu(k)+Bu＾(k+1k)

?

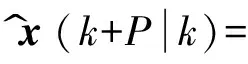
x＾(k+Pk)=

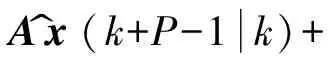
Ax＾(k+P-1k)+

Bu＾(k+P-1k)=

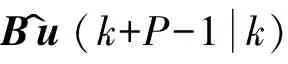
Bu＾(k+P-1k)

u＾

(

k

+

i

|

k

)=0．

根據輸出與狀態的關系y(k)=Cx(k)，得到對輸出的P步預測可表示為

(2)

其中

U＾(k)=u＾(kk)?u＾(k+M-1k)?è?????÷÷÷

約束優化的約束條件為

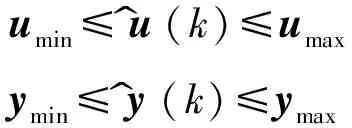
umin≤u＾(k)≤umaxymin≤y＾(k)≤ymax

由式(2)，約束條件可寫為

Umin≤U＾(k)≤UmaxYmin-Y0(k)≤SUU＾(k)≤Ymax-Y0(k)

(3)

1.2 操作變量轉換為前饋變量

實際生產過程中，因生產需要，會放開對部分操作變量的控制，此部分變量則轉換為前饋變量．

將式(1)的狀態空間表示為

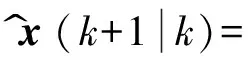
x＾(k+1k)=

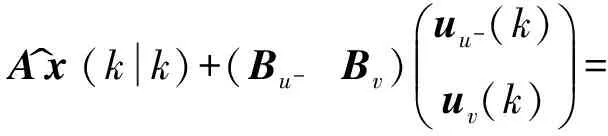
Ax＾(kk)+(Bu-Bv)uu-(k)uv(k)?è????÷÷=

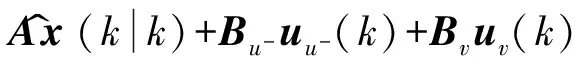
Ax＾(kk)+Bu-uu-(k)+Bvuv(k)

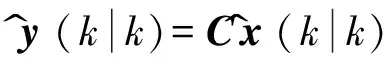
y＾(kk)=Cx＾(kk)

(4)

式中：uu-(k)∈Rm-j表示操作變量，uv(k)∈Rj表示轉換為前饋變量的部分．系數矩陣A∈Rn×n,Bu-∈Rn×(m-j),Bv∈Rn×j,C∈Rr×n．

u＾

(

k

+

i

|

k

)=0．

根據輸出與狀態的關系y(k)=Cx(k)，對輸出的P步預測可表示為

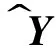
Y＾

dis

(

k

)=

S

x

x

(

k

)+

S

u-

u

u-

(

k

)+

S

v

u

v

(

k

)=

Y

0

(

k

)+

S

U-

U＾

u-

(

k

)+

S

v

U

v

(

k

)

(5)

其中

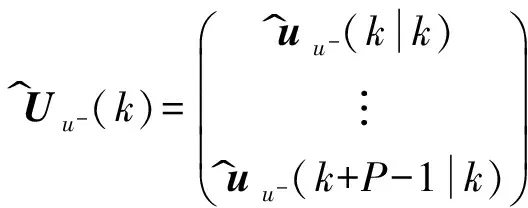
U＾u-(k)=u＾u-(kk)?u＾u-(k+P-1k)?è?????÷÷÷

約束優化的約束條件為

umin≤u＾u-(k)≤umaxymin≤y＾dis(k)≤ymax

可寫為

Umin≤U＾u-(k)≤UmaxYmin≤Ydis(k)≤Ymax

根據式(5)，約束空間可寫為

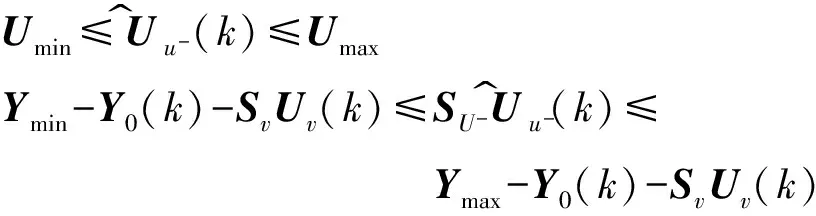
Umin≤U＾u-(k)≤UmaxYmin-Y0(k)-SvUv(k)≤SU-U＾u-(k)≤Ymax-Y0(k)-SvUv(k)

(6)

對比式(3)和(6)可以看出，輸出約束空間部分操作變量轉換成前饋變量后，產生了SvUv(k)的平移．同時由于操作變量的減少，映射到輸入約束空間的維數也隨之減少，與輸入約束空間的交集，即可行域，也因此發生變化．可見，操作變量轉換為前饋變量會對系統的可行域造成影響．

1.3 前饋變量轉換回操作變量

根據生產需要，系統有時需要將部分轉換的前饋變量轉換回操作變量．前饋變量轉換回操作變量時，若變量仍在原約束范圍內，則可將此部分前饋變量直接轉換為操作變量．

將前饋變量做如下轉換：

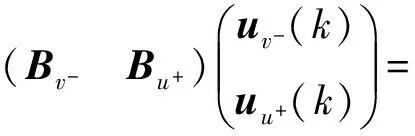
代入式(4)中，得到

x＾(k+1k)=

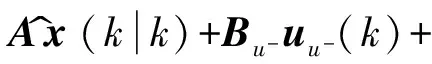
Ax＾(kk)+Bu-uu-(k)+

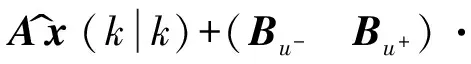
Ax＾(kk)+(Bu- Bu+)·

Ax＾(kk)+Buv+uv+(k)+

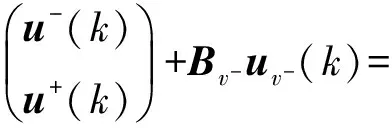
y＾(kk)=Cx＾(kk)

輸出的P步預測可表示為

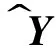
Y＾

dis-

(

k

)=

S

x

x

(

k

)+

S

v+

u

v+

(

k

)+

S

v-

u

v-

(

k

)=

Y

0

(

k

)+

S

v+

U＾

v+

(

k

)+

S

v-

U

v-

(

k

)

(7)

約束優化的約束條件

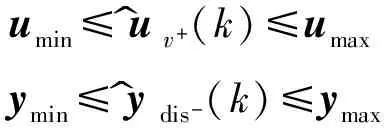
umin≤u＾v+(k)≤umaxymin≤y＾dis-(k)≤ymax

可寫為

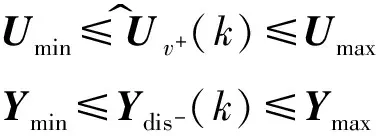
Umin≤U＾v+(k)≤UmaxYmin≤Ydis-(k)≤Ymax

根據式(7)，約束空間可寫為

(8)

對比式(8)和(6)可以看出，前饋變量在約束空間內轉換為操作變量時，操作變量維數增加，輸出約束空間映射到輸入約束空間的維數也增加．前饋變量減少，輸出約束空間的平移量也隨之減少．系統的可行域由于以上兩參數的變化，將隨之發生變化．

當前饋變量當前時刻的值超出了原約束范圍，直接轉換為操作變量時系統可能無法盡快將其控制到約束范圍內甚至系統失控．此種情況下可在不影響系統輸出的前提下放寬該操作變量的約束范圍再進行轉換．

2 變量轉換對系統可行域變化的影響機制

上一章中討論了系統變量轉換對可行域的影響，由于實際過程中變量較多，系統約束空間維數較大，很難通過數據直接判斷當前時刻進行變量轉換后系統是否還能存在可行域，下面將以雙輸入雙輸出系統為例，通過幾何作圖直觀地分析變量轉換對系統可行域的影響機制．

2.1 變量轉換對系統可行域影響的幾何描述

選取系統輸入為u1、u2，輸出為y1、y2，輸入約束范圍為u1min≤u1≤u1max和u2min≤u2≤u2max，輸出約束范圍為y1min≤y1≤y1max和y2min≤y2≤y2max．根據式(3)，系統的可行域可以表示為輸出約束空間映射到輸入約束空間的交集部分．幾何表現如圖1所示．

將操作變量u2轉換為前饋變量時，輸入約束空間由之前的二維空間變為只有u1min≤u1≤u1max的一維空間，輸出約束空間映射輸入約束空間后也變為一維空間，當前時刻交集部分為系統的可行域，幾何表現如圖2所示．

圖1 系統可行域幾何示意圖

圖2 操作變量轉換為前饋變量后系統可行域的變化

由于系統為線性系統，將u2變化造成的系統可行域變化的軌跡連線，可得到系統可行域的變化規律，如圖3所示．

圖3 隨u2變化系統可行域變化軌跡連線

比較圖3與圖1可以看出，變量轉換后，系統的可行域由轉換的變量當前值決定，隨著轉換后前饋變量的變化，系統的可行域也隨之變化．當u2超過圖中u2min和u2max范圍后，系統將無可行域．

2.2 變量轉換對預測控制可行域大小的影響

變量轉換對可行域的變化影響可分為以下幾種形式．

(1)可行域變小

多數情況下，操作變量轉換為前饋變量后，系統的可行域是變小的．由于操作變量的減少，輸入約束空間維數降低，與輸出約束空間映射到輸入約束空間的交集空間維數也相應減少．對于可行域較小的系統，若變量轉換使得系統可行域變小，可能導致系統不穩定或無法正常運行，在實際生產中不建議將此部分操作變量轉換．

(2)可行域不變

當輸出約束空間映射到輸入約束空間的部分與輸入約束空間相交的部分恰好為轉換的變量，系統只能在此部分變量的固定值處穩定運行．將此部分變量放開控制的時刻，系統可行域不變，幾何表現形式如圖4所示．

輸出約束映射區間與輸入約束空間的交集在操作變量u2的約束邊際，可行域只有u2約束邊際的線段，當u2轉換為前饋變量時，系統可行域仍為此線段，未發生變化．

此種情況下當u2轉換為前饋變量發生變化后，輸出約束空間經過線性平移系統可行域甚至增加．

實際生產中，若系統為此種情況，操作變量轉換為前饋變量對系統的穩定性不產生影響，甚至系統能更穩定，為減少控制器壓力，可長期放開對此部分操作變量的控制作用．

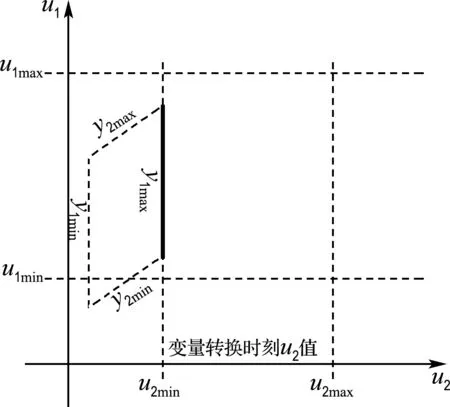
圖4 變量轉換時系統可行域不變

3 仿真實例

以Shell重油分餾塔為例[24]，模型傳遞函數矩陣為

其中，傳遞函數中各變量已經過量綱一化處理，時間常數單位為min，采樣周期為4 min．假設系統初始輸出為零．

選取模型的3個操作變量和3個被控變量，選取其中1個操作變量，放開控制器對其的控制，使其轉換為前饋變量，穩定后將此變量再轉換回操作變量．對各變量轉換前后的狀態進行仿真．各變量含義見表1．

表1 被控變量與操作變量

操作變量的約束范圍均為[-0.5,0.5]，被控變量約束范圍

y1∈[-0.5,0.5],y2∈[-0.5,0.5],

y3∈[-0.5,0.1]

系統被控目標為

y1∈[0.3,0.4],y2∈[0.3,0.4],

y3∈[-0.3,-0.151 5]

對系統變量轉換情況進行仿真，結果如圖5所示．其幾何表現形式如圖6所示．

圖5 變量轉換對系統的影響

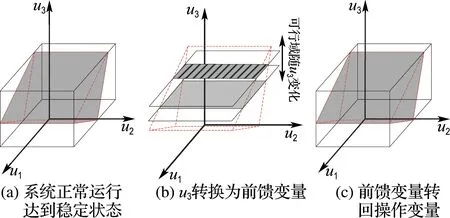
圖6 變量轉換對系統可行域影響幾何示意圖

仿真過程分為4個階段：

(1)開車到穩定運行階段：系統在控制器的控制下達到穩定狀態，輸出結果y1=0.3，y2=0.35，y3=-0.1，在系統的控制目標范圍內，并且穩定運行．其可行域幾何示意圖如圖6(a)所示．

(2)穩定運行狀態到發生變量轉換：當t=350 min時，放開控制器對操作變量u3的控制，操作變量u3轉換為前饋變量．變量發生轉換后，系統的輸入約束空間發生變化，維數減少，映射矩陣由三維變為二維，可行域范圍由原來的u1、u2、u3組成的三維空間變為u1、u2組成的平面，可行域減小，幾何示意圖如圖6(b)所示．由于可行域減小，系統無法在最優可行解處取值，系統的輸出無法達到最佳的設定值，系統的輸出結果發生變化．

(3)前饋變量發生階躍：在t=550 min時，給前饋變量一個10%的階躍，前饋變量的變化使得系統的可行域發生前饋變量u3方向的平移，系統可行域變得更小，操作變量取值離最優解距離發生更大的變化，導致系統的輸出無法穩定在設定值范圍內．其可行域幾何示意圖如圖6(b)所示．

(4)前饋變量u3轉回操作變量：在t=880 min時，將前饋變量轉換回操作變量．由于前饋變量u3仍在原操作變量的約束范圍內，根據本文的分析，前饋變量轉回操作變量，系統仍能穩定運行并回到轉換前的穩定狀態．由仿真結果可以看出，系統的輸出與變量轉換前穩定運行狀態的輸出結果一致，驗證了在變量不超出其約束范圍的情況下，該變量可以在任意時刻轉換回操作變量的結論．該階段可行域幾何示意圖如圖6(c)所示．

4 結 語

本文從實際生產中存在的變量間相互轉換的實際情況出發，利用映射和空間幾何的思想，分析研究得出了操作變量與前饋變量轉換對控制系統可行域的影響機制．變量轉換后系統可行域維度發生變化，對系統的穩定性甚至可控性有明顯的影響．轉換的變量若仍在原有約束范圍內變化，則系統仍能達到穩定狀態，并且該變量可轉換回操作變量；若轉換的變量超出約束范圍，則會使系統失控．因此，針對實際生產中的需要，在放開控制器對某些操作變量的控制前，應先分析此部分操作變量與前饋變量的轉換對系統可行域的影響，確定系統的可控性．

[1] 席裕庚,李德偉,林 姝. 模型預測控制——現狀與挑戰[J]. 自動化學報, 2013, 39(3):222-236.

XI Yugeng, LI Dewei, LIN Shu. Model predictive control-status and challenges [J]. Acta Automatica Sinica, 2013, 39(3):222-236. (in Chinese)

[2] 王 可,董從建,張 博. 模型預測控制工業應用及發展研究[J]. 信息通信, 2013(4):31.

WANG Ke, DONG Congjian, ZHANG Bo. Application and development of model predictive control [J]. Information & Communications, 2013(4):31. (in Chinese)

[3] 劉向杰,孔小兵. 電力工業復雜系統模型預測控制——現狀與發展[J]. 中國電機工程學報, 2013, 33(5):79-85.

LIU Xiangjie, KONG Xiaobing. Present situation and prospect of model predictive control application in complex power industrial process [J]. Proceedings of the CSEE, 2013, 33(5):79-85. (in Chinese)

[4] TOMIZUKA M. Model based prediction, preview and robust controls in motion control systems [C] // 1996 4th International Workshop on Advanced Motion Control. Piscataway: IEEE, 1996.

[5] DARBY M L, NIKOLAOU M. MPC:Current practice and challenges [J]. Control Engineering Practice, 2012, 20(4):328-342.

[6] MAYNE D Q, RAWLINGS J B, RAO C V,etal. Constrained model predictive control:Stability and optimality [J]. Automatica, 2000, 36(6):789-814.

[7] 劉雨波,羅雄麟,許 鋒. 分布式預測控制全局協調及穩定性分析[J]. 化工學報, 2013, 64(4):1318-1331.

LIU Yubo, LUO Xionglin, XU Feng. Global coordination and stability analysis for distributed model predictive control system [J]. CIESC Journal, 2013, 64(4):1318-1331. (in Chinese)

[8] 鄒 濤,李海強,丁寶蒼,等. 多變量預測控制系統穩態解的相容性與唯一性分析[J]. 自動化學報, 2013, 39(5):519-529.

ZOU Tao, LI Haiqiang, DING Baocang,etal. Compatibility and uniqueness analyses of steady state solution for multi-variable predictive control systems [J]. Acta Automatica Sinica, 2013, 39(5):519-529. (in Chinese)

[9] 楊 罡. 電力系統模型預測控制技術研究[D]. 北京:北京交通大學, 2013.

YANG Gang. Research on power system model predictive control technology [D]. Beijing:Beijing Jiaotong University, 2013. (in Chinese)

[10] 席裕庚. 復雜工業過程的滿意控制[J]. 信息與控制, 1995, 24(1):14-20.

XI Yugeng. Satisfactory control of complex industrial process [J]. Information and Control, 1995, 24(1):14-20. (in Chinese)

[11] VALENCIA-PALOMO G, ROSSITER J A, LPEZ-ESTRADA F R. Improving the feed-forward compensator in predictive control for setpoint tracking [J]. ISA Transactions, 2014, 53(3):755-766.

[12] NUNEZ-REYES A, NORMEY-RICO J E, BORDONS C,etal. A Smith predictive based MPC in a solar air conditioning plant [J]. Journal of Process Control, 2005, 15(1):1-10.

[13] ROSSITER J A. Model-based Predictive Control-A Practical Approach [M]. London: CRC Press, 2004.

[14] 王永賓,許 軍,周奇勛. 改進重置粒子群算法在MPC調速系統中的應用[J]. 微電機, 2015, 48(5):79-84.

WANG Yongbin, XU Jun, ZHOU Qixun. Application of improved reinitialization PSO for MPC in speed control system [J]. Micromotors, 2015, 48(5):79-84. (in Chinese)

[15] 李奇安,李 平,于海斌,等. 串聯系統的多前饋-反饋廣義預測控制[J]. 控制與決策, 2002, 17(4):402-406.

LI Qi′an, LI Ping, YU Haibin,etal. Multiple feed-forward and feedback generalized predictive control for cascade system [J]. Control and Decision, 2002, 17(4):402-406. (in Chinese)

[16] 于 洋,許 鋆,羅雄麟. 預測控制約束邊界效應與解決方法研究[J]. 自動化學報, 2014, 40(9):1922-1932.

YU Yang, XU Jun, LUO Xionglin. Constraint boundary effect in model predictive control and corresponding solution [J]. Acta Automatica Sinica, 2014, 40(9):1922-1932. (in Chinese)

[17] GRAICHEN K, PETIT N. Incorporating a class of constraints into the dynamics of optimal control problems [J]. Optimal Control Applications and Methods, 2009, 30(6):537-561.

[18] 杜曉寧. 預測控制新型優化策略的研究及分析[D]. 上海:上海交通大學, 2001.

DU Xiaoning. Study and analysis on new optimization strategy of predictive control [D]. Shanghai:Shanghai Jiao Tong University, 2001. (in Chinese)

[19] 李德偉,席裕庚,秦 輝. 預測控制等效集結優化策略的研究[J]. 自動化學報, 2007, 33(3):302-308.

LI Dewei, XI Yugeng, QIN Hui. An equivalent aggregation optimization strategy in model predictive control [J]. Acta Automatica Sinica, 2007, 33(3):302-308. (in Chinese)

[20] 張惜嶺,王書斌,羅雄麟. 化工過程約束優化控制的可行性分析及約束處理[J]. 化工學報, 2011, 62(9):2546-2554.

ZHANG Xiling, WANG Shubin, LUO Xionglin. Feasibility analysis and constraints adjustment of constrained optimal control in chemical processes [J]. CIESC Journal, 2011, 62(9):2546-2554. (in Chinese)

[21] 張 佳,羅雄麟,許 鋒,等. 前饋變量對預測控制可行域的影響分析[J]. 化工學報, 2016, 67(9):3776-3783.

ZHANG Jia, LUO Xionglin, XU Feng,etal. Influence of feed forward variables on feasible region of model predictive control [J]. CIESC Journal, 2016, 67(9):3776-3783. (in Chinese)

[22] 羅雄麟,周曉龍,王書斌. 輸入變量關聯約束對約束優化控制的影響特性分析[J]. 自動化學報, 2013, 39(5):679-689.

LUO Xionglin, ZHOU Xiaolong, WANG Shubin. Analysis of constrained optimal control with related constraints of input variables [J]. Acta Automatica Sinica, 2013, 39(5):679-689. (in Chinese)

[23] 羅雄麟,周曉龍,王書斌,等. 多約束狀態過程的區間預測控制[C] // 第三十一屆中國控制會議論文集. 合肥:中國科學技術大學出版社, 2012:4062-4068.

LUO Xionglin, ZHOU Xiaolong, WANG Shubin,etal. Zone control with model predictive control for much constrained states process [C] // Proceedings of the 31st Chinese Control Conference. Hefei: Press of University of Science and Technology of China, 2012:4062-4068. (in Chinese)

[24] 羅雄麟,周曉龍,朱麗萍. 參考軌跡在線優化的區間預測控制[J]. 控制工程, 2013, 20(3):223-226, 230.

LUO Xionglin, ZHOU Xiaolong, ZHU Liping. Zone model predictive control with online optimization of reference trajectory [J]. Control Engineering of China, 2013, 20(3):223-226, 230. (in Chinese)

Influential mechanism of switch between manipulated variables and feed-forward variables on feasible region of model predictive control

LUO Xionglin*, ZHANG Jia, XU Feng, XU Jun

( Department of Automation, China University of Petroleum, Beijing 102249, China )

Model predictive control is widely used in process control because of its decoupling ability and strong robustness. In the actual industrial process, considering operation requirements, a part of manipulated variables are released by controller and transformed into feed-forward variables at the same time. The transformation between manipulated variables and feed-forward variables results in structure changing among different systems, including square system, fat system and thin system. For the thin system, in which the dimension of manipulated variables is less than that of the controlled variables, the control result is usually less effective than the others. Besides, the partial original manipulated variables, released by controller, transformed into feed-forward variables, also affect the control performance. Feasible region can reflect the effect of the control system directly. On the basis of the multi-step prediction formula derivation for state space model, the method of spatial geometry mapping is used to express the transformation between manipulated variables and feed-forward variables. In addition, it is also used to analyze the influence on the change of feasible region caused by the transformation. Finally, aiming at the situation for releasing partial manipulated variables, prejudgment method is proposed to ensure the stability.

process control; model predictive control; feed-forward variables; feasible region

1000-8608(2017)03-0308-08

2016-09-23；

2017-03-16．

國家自然科學基金資助項目(21676295);“九七三”國家重點基礎研究發展計劃資助項目(2012CB720500).

羅雄麟*(1963-)，男，博士，教授，E-mail:luoxl@cup.edu.cn.

TP273

A

10.7511/dllgxb201703014