微積分在大學物理中的運用
王志潤
【摘要】微積分是大學物理學習的重點,依據現階段大學物理教學工作情況為基礎,結合近年來微積分實施特點,分析微積分在大學物理中的應用,明確微積分在大學物理中的重要性,并結合實際案例明確應用的方向。
【關鍵詞】微積分 大學 物理 運用
【中圖分類號】G64 【文獻標識碼】A 【文章編號】2095-3089(2017)14-0177-01
大學物理中微積分擁有較為寬泛的應用,是重要的教學依據,依據微積分獲取物理大膽,是大學物理教學工作的重難點,不容易理解和掌控。大學物理中不管是質地力學、剛體的定軸轉變、熱力學基礎,還是靜電場、磁場等都是依據微積分解決問題。因為學生在中學時期依據代數計算簡單的物理知識,在大學之后,大學物理知識的學習也可以引導學生從代數運算理解物理知識轉變為微積分理解物理知識。
一、微積分理念在大學物理中的必要性
大學物理中不管是質點力學、剛體的定軸轉變、熱力學基礎,還是靜電場、磁場都需要結合微積分解決問題,理解基礎物理知識。因為學生在中學時期主要是依據點數計算來研究簡單的物理知識和問題,在進入到大學時期之后,大學物理知識的學習將從以往代數計算形式轉變為微積分計算方案,以此更好理解復雜的物理知識和問題。積分是大學物理教學中經常應用的工具之一,若是可以靈活引用掌控積分理念和方案,就可以加單的獲取實際物理知識和問題的答案[1]。
二、微積分在大學物理中的應用
其中主要分為以下幾點:第一,導數方法。導數是一個量在某一點附近的變化效率,解決物理問題的過程中需要依據導數獲取物理量的變化效率。第二,微分方案。其包含了變與不變的辯證聯系、整體與局部的關系。將復雜的物理問題劃分多個層次,促使局部范圍無線小,也就是微分,將所有無限多個微元的結果求和,就是積分。微分就是依據微元法解決較為復雜的物理知識。將整體氛圍多個微小區域,變量作為產量實施解決,促使問題變的較為簡單。第三,積分方案。積分與微積分彼此為逆運算,積分就是獲取微分的和值。積分途徑和積分上下限的選擇不但要滿足自然規則,并且盡量單一以此降低計算數量。積分方案在力學、電學等知識中得到了有效的引用。第四,微分方程方案。其實依據未知函數的導數和自變量之間的方程,其推廣較為寬廣。在力學、天文學以及量子力學等有非常多的引用。第五,近似計算方案。其是一種經常應用的解題方案,在解決物理知識的過程中得到了有效的引用。
三、案例分析
例一,質點依據直線運動,加速度為4-t2,式中各量都是SI制,已知t1=0時速度為10m/s,求t2=3s時的速度。
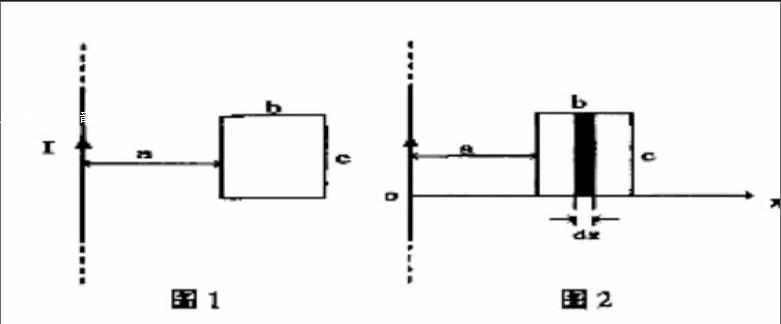
例二,如圖1,已知載流長直導線的電流為I,求通過矩形面積的磁通量。
例三,質點在外力F=F0-■x的作用下沿著ox軸運動,其中Fo、I是常量,求質點從x1=0運動到x2=I的過程中力F所作的功。
在例一中,加速度在時間t1到t2中隨著時間的變化,不再存在恒定;例二中磁感強度的大小與到直導線的距離相關,會依據面積S上位置的差異性而產生變化,不再是平衡劃分的。例三,力會隨著位置的差異性而產生變化,不再是恒力。由此可見,依據上述三個案例的物理情境與中學教學的情境存在差異性,物理情感的變化也會導致中學學習的初級公式v=vo+at等難以在上述案例中應用,因為初級公式都是構建在加速度等是恒定不變的基礎上,但是加速度等數值隨著時間或空間變化產生變化時,相關的公式也難以引用。解決這些問題的方案,之后將其無限劃分為多個部分目標dt、d、向量S、d、向量r,每一個劃分之后的局部都具備向量加速度等數值恒定的特點[2]。
四、結束語
總而言之,微積分在大學物理中的引用,不但是數學教學形式的引用,還是一種思維形式的引用,依據實際教學工作有助于學生可以將現實復雜物理知識轉變為更好理解的知識,促使其劃分為較小時間或者是空間的區域問題,之后在集零為整,將區域問題集中起來,依據微積分在大學物理中的引用,最后學生可以具備優質的微積分引用教學方案,以此解決中學教學階段無法解決的物理知識和問題,以此激發學生學習物理知識的興趣,提升實際物理課堂教學質量和效率。
參考文獻:
[1]朱葉青.微積分在大學物理教學中的重要應用[J]. 科技視界,2014,(22).
[2]馬新澤.淺析大學物理中的微積分教學[J]. 昌吉學院學報,2015,(02).

