行星齒輪箱典型故障對內齒圈齒根應變的作用機理研究

牛 杭， 張小棟1,, 趙欣丹， 侯成剛

(1. 西安交通大學 現代設計及轉子軸承系統教育部重點實驗室， 西安 710049；2. 西安交通大學 機械工程學院， 西安 710049)

行星齒輪箱典型故障對內齒圈齒根應變的作用機理研究

牛 杭2， 張小棟1,2, 趙欣丹2， 侯成剛2

(1. 西安交通大學 現代設計及轉子軸承系統教育部重點實驗室， 西安 710049；2. 西安交通大學 機械工程學院， 西安 710049)

行星齒輪箱由于具有優良的特性被廣泛應用于多領域的機械傳動系統中，但惡劣的工作條件導致其故障頻發，因此開展行星齒輪箱故障診斷方法的研究工作十分必要。傳統的基于振動信號的故障診斷方法在識別行星齒輪箱早期微弱故障方面具有局限性，為此提出基于內齒圈齒根應變信號的行星齒輪箱故障診斷方法，并主要開展行星齒輪箱典型故障對內齒圈齒根應變的作用機理研究工作。分析行星齒輪箱內齒圈齒根應變模型的構建方法，將內齒圈齒根應變模型分解為行星輪-內齒圈嚙合力模型、內齒圈輪齒的齒形系數模型和齒間載荷分配系數模型；利用行星齒輪箱的純扭轉模型計算行星輪-內齒圈嚙合力，利用材料力學理論推導內齒圈輪齒的齒形系數，并對行星輪-內齒圈嚙合過程中的齒間載荷分配系數進行分析；研究行星齒輪箱典型故障對嚙合剛度的影響，并根據內齒圈齒根應變模型計算得到典型故障下內齒圈齒根應變的變化規律。建模仿真計算分析結果表明，不同類型、不同部位、不同劇烈程度的故障會對行星齒輪箱內齒圈齒根應變信號造成不同影響，利用內齒圈齒根應變信號可有效識別行星齒輪箱的故障行為。

行星齒輪箱； 內齒圈； 齒根應變； 振動； 故障診斷

行星齒輪箱由于體積小、重量輕、傳動效率高、承載能力強等優點被廣泛用于航空航天、風力發電、起重運輸等領域的機械傳動系統中。通常行星齒輪箱工作在低速重載的惡劣環境下，其關鍵部件出現故障的概率很高，為了減少事故發生，降低維修成本，開展行星齒輪箱的故障診斷工作十分必要。

目前，行星齒輪箱的故障診斷方法主要是振動分析法。振動信號中包含有豐富的故障信息，是一種常用的機械設備故障特征載體信號，然而，行星齒輪箱的振動信號相比于一般機械設備具有更加復雜的特點。由于測量振動信號的加速度傳感器在箱體上固定不動，而行星輪卻在公轉，所以傳感器測到的多組振動信號的強度會被傳輸路徑調制，并且由于各振動信號之間存在相位差[1]，當這些振動信號在傳感器處相互耦合時，會出現矢量疊加效應，影響振動信號中各頻率成分的幅值[2]，從而導致故障特征頻率成分可能減小或消失；另外，變速、變載的工況會對振動信號的幅值造成影響，轉速波動會使振動信號的頻譜表現模糊，故障特征頻率發生變化。由于行星齒輪箱振動信號的這種非線性和非平穩性特點，雖然近年國內外學者取得了一些非常有價值的研究成果[3-7]，但從實際工況下的振動信號中提取行星齒輪箱的早期微弱故障特征仍是一個技術難題。

從動力學角度分析不難發現，行星齒輪箱故障首先會造成嚙合狀態變化，進而才會導致振動信號變化，振動信號是反映嚙合狀態的一種間接信號。已有的研究表明行星齒輪箱振動信號與嚙合狀態信息之間具有非常復雜的映射關系，這種映射關系的復雜性本質上導致了基于振動信號的行星齒輪箱故障診斷方法的局限性。為了突破這一困境，除了繼續深入開展上述研究外，尋找更加優質的故障特征載體信號將是一種更為有效的途徑。

由于行星輪-內齒圈嚙合狀態會直接影響內齒圈齒根應變，行星輪-太陽輪嚙合狀態會通過行星輪間接影響內齒圈齒根應變，所以與振動信號相比，內齒圈齒根應變信號與嚙合狀態信息之間具有更加直觀、明確的對應關系，理論上可以更好地反映行星齒輪箱的健康狀態。本課題組自2003年起至今一直從事光纖動態檢測技術的研究工作[8]，并于近兩年提出了基于光纖光柵的齒根應變檢測方法[9]，且就結構件應力應變的光纖光柵動態測量技術進行了實驗研究[10]，該方法克服了現有的光彈法和電測法的不足，為內齒圈齒根應變的在線分布式測量提供了解決途徑。本文將著重展開行星齒輪箱典型故障對內齒圈齒根應變的作用機理研究，旨在為基于內齒圈齒根應變的行星齒輪箱故障診斷方法提供理論依據。

在齒根應力應變研究方面，國內外學者多針對一對齒輪嚙合的情況，分析不同設計參數對輪齒彎曲強度的影響[11-12]，這些研究沒有從行星齒輪箱系統角度考慮問題，因此，難以解釋行星齒輪箱故障和內齒圈齒根應變的關系。本文首先討論行星齒輪箱內齒圈齒根應變的建模方法，然后分別對行星輪-內齒圈嚙合力、內齒圈輪齒的齒形系數和齒間載荷分配系數等三個子模型進行分析研究，以完成內齒圈齒根應變模型的構建。最后，針對行星輪、太陽輪、內齒圈上存在的不同形式常見故障，通過仿真分析的手段，分別討論不同類型、不同位置以及不同劇烈程度的故障對內齒圈齒根應變的影響。

1 內齒圈齒根應變建模方法研究

如圖1所示，對于行星齒輪箱內齒圈某一輪齒ζ而言，其齒根應變由輪齒ζ的齒形以及分配到輪齒ζ的嚙合力兩個因素主要決定。

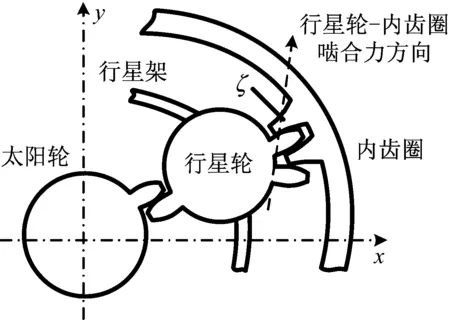
圖1 行星齒輪箱結構示意圖

輪齒ζ從進入嚙合到退出嚙合的過程中，嚙合點位置變化，嚙合剛度變化，導致行星輪-內齒圈嚙合力以及輪齒間載荷的分配情況變化，所以即便外界載荷不變，輪齒ζ的齒根應變仍呈現時變特點，其模型如式(1)所示

ε(t)=KYF(t)Xr(t)Frpi(t)

(1)

式中:ε(t)為內齒圈某一輪齒的齒根應變；K為應變修正系數，該值為常數；YF(t)為齒形系數，描述不同嚙合位置處的齒形信息；Xr(t)為齒間載荷分配系數，描述分配到內齒圈分析輪齒上的行星輪-內齒圈嚙合力所占的比例；Frpi(t)為行星輪-內齒圈嚙合力。

由式(1)可以看出，內齒圈齒根應變模型主要包含行星輪-內齒圈嚙合力模型、齒形系數模型以及齒間載荷分配系數模型。以下分別針對上述三個子模型進行分析研究，以完成內齒圈齒根應變模型的構建。

2 行星輪-內齒圈嚙合力模型

圖2為2K-H型行星齒輪箱的一種純扭轉模型[13-15]，設行星輪數為N，則該模型有N+2個自由度，分別為太陽輪的扭轉自由度us、行星架的扭轉自由度uc、行星輪i的扭轉自由度upi。

根據圖2所示，行星輪i-內齒圈嚙合力可表示為如(2)式所示形式

(2)

式中:krpi為行星輪i-內齒圈的嚙合剛度；krpi為行星輪i-內齒圈的嚙合阻尼，該值為常數；Urpi為行星輪i-內齒圈的嚙合變形，Urpi=upi-uc。若求解Frpi，需得到krpi和Urpi隨時間的變化規律。

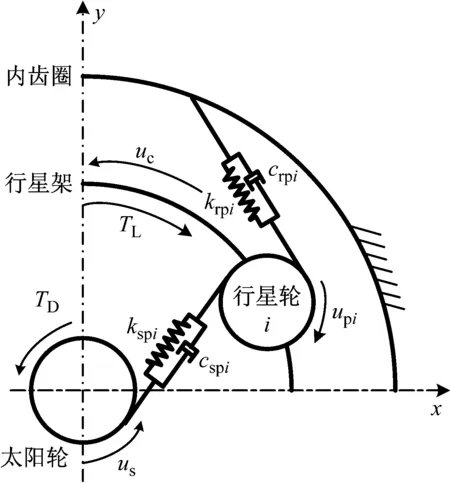
圖2 行星齒輪箱純扭轉模型

首先，建立行星輪-太陽輪和行星輪-內齒圈的嚙合剛度模型。設S(2πft+φ,τ)為頻率為f，初相位為φ，占空比為τ的方波信號，且ksp1的初相位為0，則行星齒輪箱的嚙合剛度可以表示為如式(3)所示形式

(3)

然后，求解行星輪i-內齒圈嚙合變形Urpi。建立如式(4)所示的動力學模型

(4)

式中:J為轉動慣量，下標s，c，pi分別表示太陽輪、行星架、行星輪i；Uspi為行星輪i-太陽輪的嚙合變形，Uspi=us-upi-uc；cspi為行星輪i-太陽輪的嚙合阻尼；mpai為行星輪i的質量；rs為太陽輪的基圓半徑；rpi為行星輪i的基圓半徑；rc為行星架半徑；rbc為行星架的當量半徑，rbc=rccosα，α為嚙合角；TD為驅動轉矩；TL為負載轉矩。

式(4)所示方程中含剛體自由度，為了消除剛體位移，引入相對坐標Uspi和Usc，其中Usc=Uspi+Urpi。引入相對坐標后，式(4)轉化為

(5)

求解式(5)，得到Uspi、Usc，則行星輪i-內齒圈的嚙合變形Urpi=Usc-Uspi。

最后，將由式(5)求得的Urpi和式(3)中的krpi代入式(2)，即可得到行星輪-內齒圈嚙合力隨時間的變化規律。

3 內齒圈齒形系數與齒間載荷分配系數模型

內齒圈上的單個輪齒的受力情況如圖3所示。

將內齒圈輪齒等效為懸臂梁，根據材料力學理論，內齒圈齒根的應變(齒面方向)可表示為如式(6)所示形式

(6)

式中，B為輪齒寬度。定義齒形系數YF如式(7)所示

(7)

式中:齒根法向弦長S;彎曲力臂h根據ISO 6336-3—2006標準[16]計算。將式(7)帶入式(6)，可得式(1)所示形式。

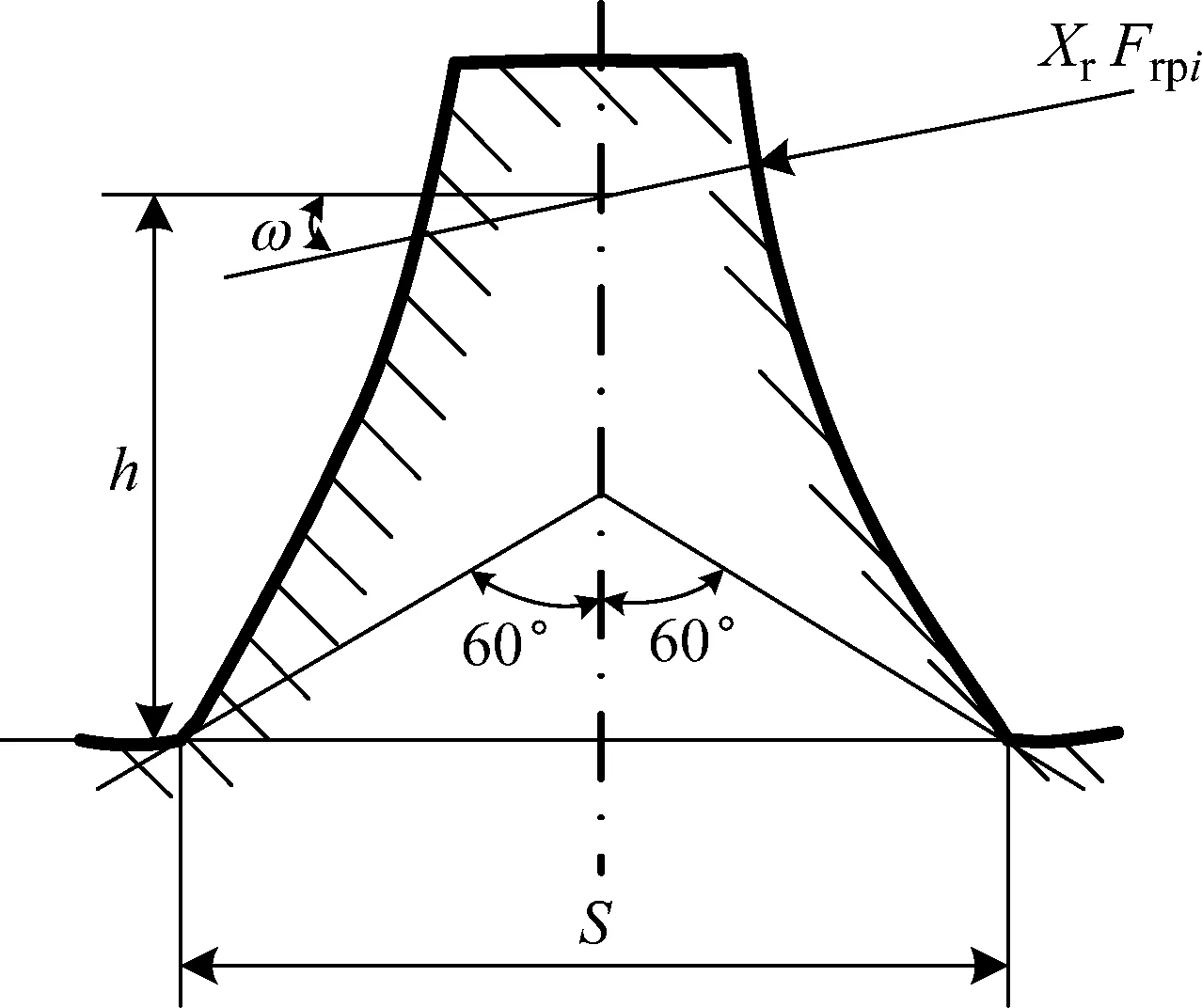
圖3 內齒圈單個輪齒的受力情況

文獻[17]通過對650組不同幾何參數的內嚙合傳動進行計算分析，發現內嚙合傳動過程中的齒間載荷分配系數形式除與齒頂高相關外，與輪齒其他幾何參數關系不大。對于標準齒頂高的情況，在內齒圈某一輪齒從進入嚙合到退出嚙合的過程中，其齒間載荷分配系數的形式如圖4所示，其中t1為內齒圈某一輪齒進入嚙合的時刻，t4為該輪齒退出嚙合的時刻，t1-t2為雙齒嚙合區時間段，t2-t3為單齒嚙合區時間段，t3-t4為雙齒嚙合區時間段。

圖4 齒間載荷分配系數

4 典型故障下內齒圈齒根應變的變化規律分析

根據文獻[18 ]和文獻[19]，當正常輪齒(如圖5(a))出現齒面剝落、輪齒缺損、裂紋故障(如圖5(b)～圖5(d))時，故障齒參與的嚙合剛度可呈現出如圖6所示的形式。

為了分析行星齒輪箱出現如圖5(b)～圖5(d)所示故障時內齒圈齒根應變變化特點，將圖6所示的嚙合剛度代入式(5)，利用4階Runge-Kutta法求解Urpi，然后將Urpi和krpi代入式(2)求解內嚙合力Frpi，最后將Frpi代入式(1)即能求解得到內齒圈齒根應變的變化規律。

(a)正常(b)齒面剝落

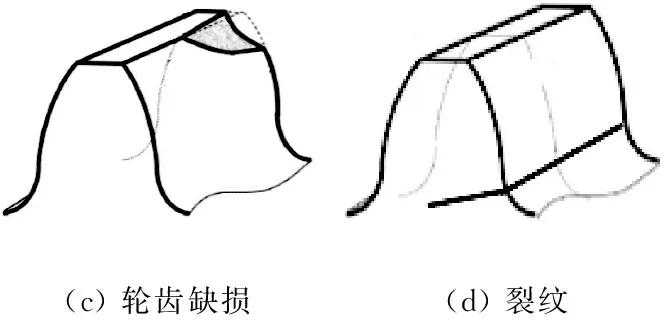
(c)輪齒缺損(d)裂紋

圖5 正常輪齒與故障輪齒形態

Fig.5 Normal gear tooth and faul gear tooth

(a) 齒面剝落

(b) 輪齒缺損

(c) 裂紋

本文所用到的行星齒輪箱參數如表1[20]所示。以下分析只針對與行星輪1發生嚙合的內齒圈輪齒的齒根應變信號，與其他行星輪發生嚙合，具有類似的分析方法。

4.1 行星輪故障對內齒圈齒根應變的影響

本節將討論在行星輪1的某個輪齒上出現的齒面剝落、輪齒缺損和裂紋等三種常見故障。

(1) 行星輪局部故障在齒根應變信號中的特征頻率分析

圖7為當行星輪出現輪齒缺損故障后，內齒圈齒根應變的變化情況，圖8為圖7在0.55～0.73 s的局部放大圖。從圖8可以明顯觀察到行星齒輪箱的嚙合頻率40 Hz(0.025 s)，且當故障齒參與嚙合時，由于嚙合剛度局部減小，內齒圈齒根應變出現異常。從圖7可以看出，在行星輪的一個自轉周期(1.025 s)內，內齒圈齒根應變出現了時間間隔為半個行星輪自轉周期(0.512 5 s)的兩個異常位置，每個異常出現的頻率為行星輪的自轉頻率(0.98 Hz)。這兩個異常嚙合出現的原因不同，第一個異常是由行星輪故障齒和內齒圈輪齒嚙合導致的，第二個異常是由行星輪故障齒和太陽輪輪齒嚙合導致的。對于齒面剝落和裂紋故障，其特征頻率與輪齒缺損故障相同。

圖8 行星輪故障時內齒圈齒根應變信號局部放大圖

(2) 故障類型對齒根應變偏差的影響分析

針對不同的行星輪故障，內齒圈齒根應變異常形式是有明顯區別的。首先將相鄰的齒根應變信號相加，形成時域上連續的齒根應變信號，然后求正常的齒根應變連續時域信號與故障下的齒根應變連續時域信號的偏差。

圖9所示為在三種故障下，當行星輪1的故障齒與內齒圈發生嚙合時，內齒圈齒根應變信號的偏差。從圖9可以看出，不同行星輪故障對內齒圈齒根應變信號的影響不同，每種故障所對應的齒根應變偏差與相應的時變嚙合剛度(如圖6)在形式上有一定的相關性，所以可以根據內齒圈齒根應變偏差的形式判斷不同的行星輪故障類型。

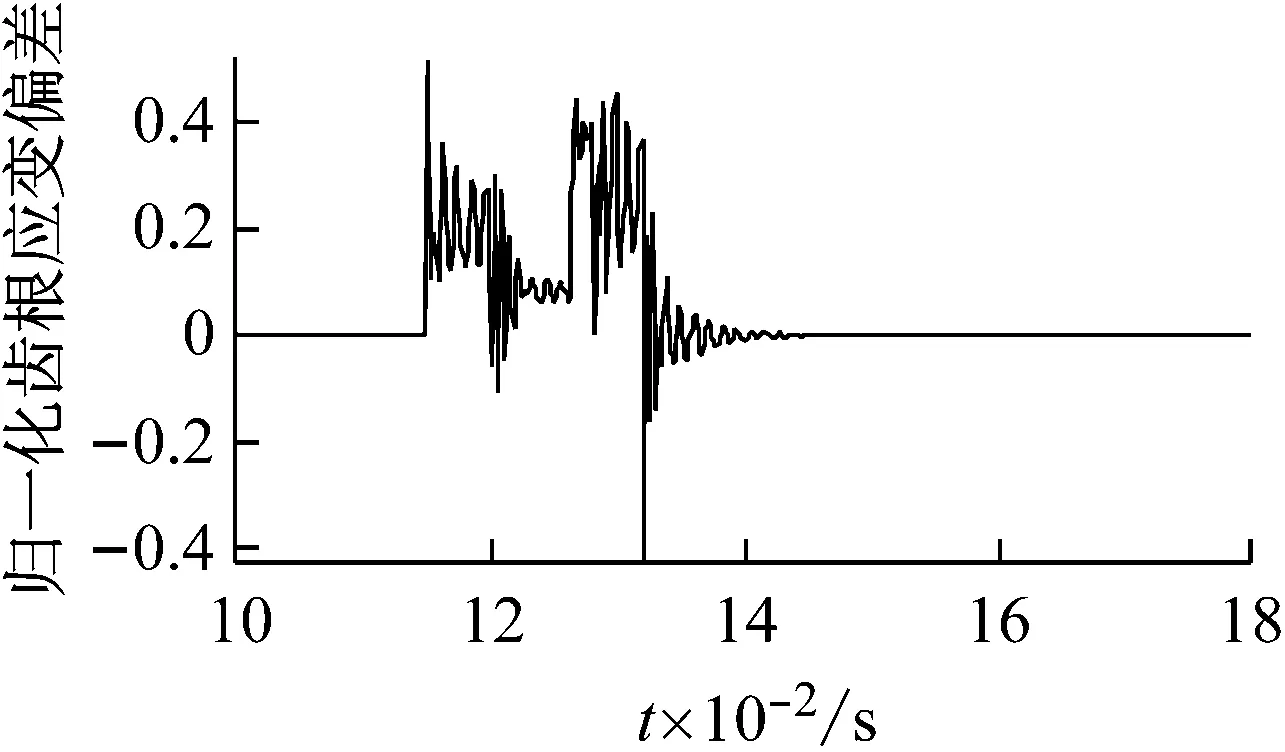
(a) 齒面剝落

(b) 輪齒缺損

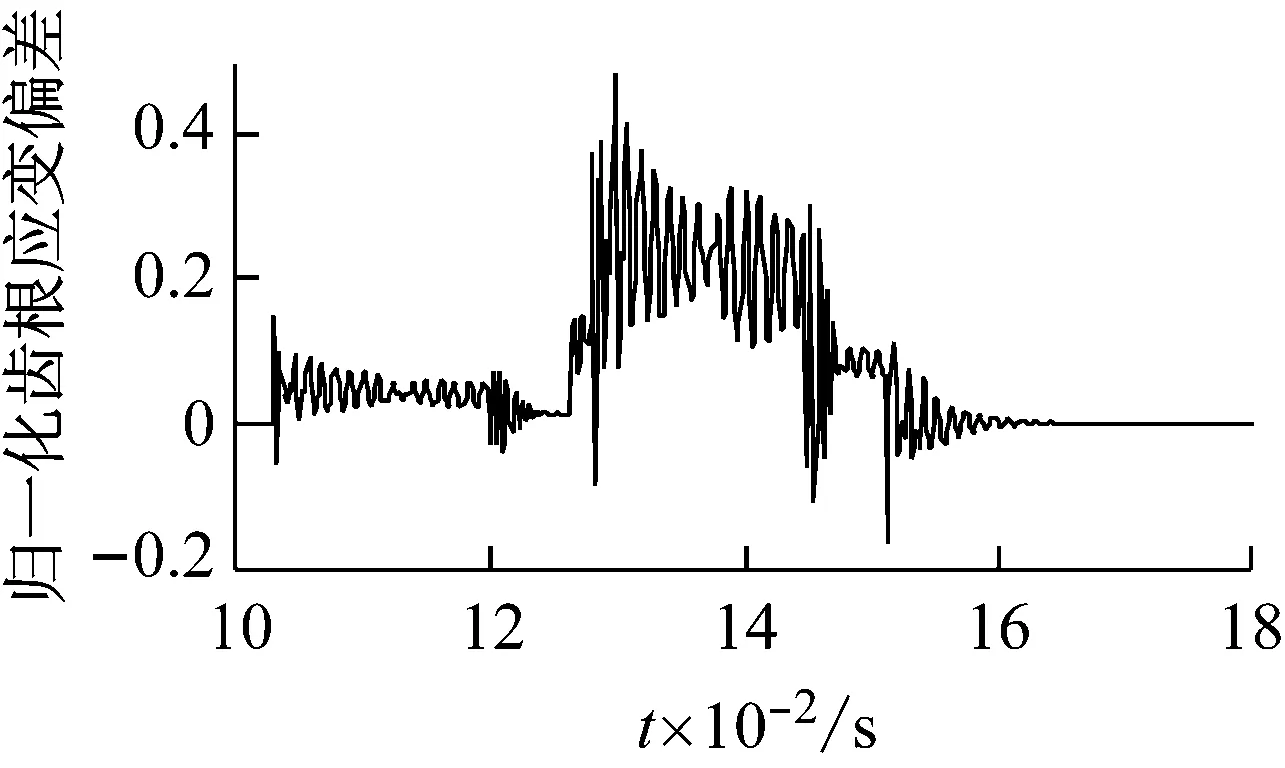
(c) 裂紋 圖9 不同行星輪故障下內齒圈齒根應變偏差

(3) 故障劇烈程度對齒根應變偏差的影響分析

針對行星輪的某一輪齒上分別存在的三種深度不同的裂紋，其對嚙合剛度的影響如圖10所示。

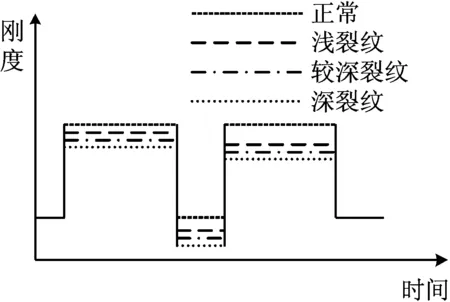
圖10 不同裂紋深度對嚙合剛度的影響

按照前文所述方法計算在三種故障劇烈程度下內齒圈齒根應變偏差，如圖11所示。由圖11可知，故障越劇烈，齒根應變偏差的能量水平越高，根據這一特點，有望實現行星齒輪箱故障的定量識別。對于齒面剝落和輪齒缺損故障，其不同劇烈程度下齒根應變信號的表現規律與裂紋故障相同。

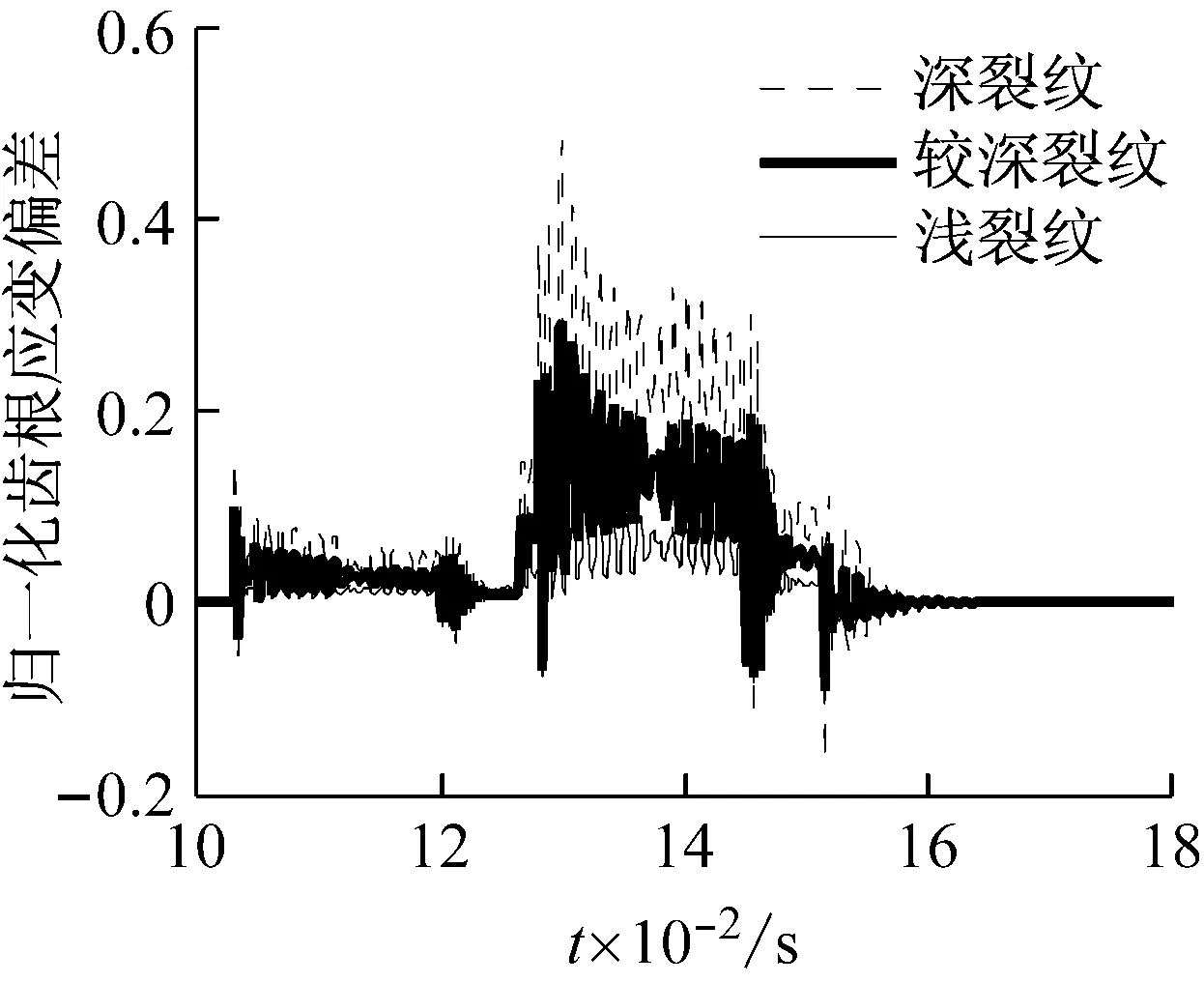
圖11 不同裂紋深度下內齒圈齒根應變偏差

4.2 太陽輪故障對內齒圈齒根應變的影響

本節將討論在太陽輪的某個輪齒上出現的齒面剝落、輪齒缺損和裂紋等三種常見故障。

圖12為當太陽輪出現輪齒缺損故障后，內齒圈齒根應變的變化情況。由圖12可知，在太陽輪相對于行星架的一個旋轉周期(0.55 s)內，內齒圈齒根應變出現了時間間隔為1/3個太陽輪相對旋轉周期(0.18 s)的三個異常位置，每個異常出現的頻率為太陽輪的相對旋轉頻率(1.8 Hz)。其中，第一個異常是由太陽輪故障齒和行星輪1嚙合導致的，第二個異常是由太陽輪故障齒和行星輪2嚙合導致的，第三個異常是由太陽輪故障齒和行星輪3嚙合導致的。

圖12 太陽輪故障時內齒圈的齒根應變信號

圖13所示為在三種故障下，當太陽輪故障齒與行星輪2發生嚙合時，內齒圈齒根應變信號的偏差。由圖13可知，不同太陽輪故障對內齒圈齒根應變信號的影響不同，每種故障所對應的齒根應變偏差與相應的時變嚙合剛度有一定的相關性，所以可以根據內齒圈齒根應變偏差的形式判斷不同太陽輪故障的類型。

對于太陽輪故障，當故障劇烈程度不同時，內齒圈齒根應變信號的表現與行星輪故障具有相同的規律，在此不再詳述。

4.3 內齒圈故障對內齒圈齒根應變的影響

本節將討論在內齒圈的某個輪齒上出現的齒面剝落、輪齒缺損和裂紋等三種常見故障。

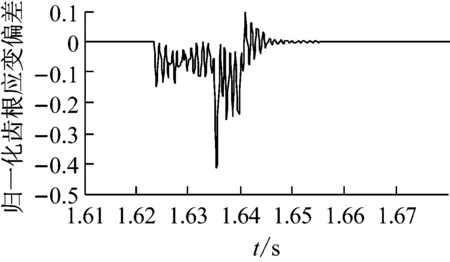
圖14為當內齒圈出現輪齒缺損故障后，內齒圈齒根應變的變化情況。由圖14可知，在行星架的一個旋轉周期(2.6 s)內，內齒圈齒根應變出現了時間間隔為1/3個行星架旋轉周期(0.87 s)的三個異常位置，每個異常出現的頻率為行星架的旋轉頻率(0.38 Hz)。其中，第一個異常是由內齒圈故障齒和行星輪1嚙合導致的，第二個異常是由內齒圈故障齒和行星輪2嚙合導致的，第三個異常是由內齒圈故障齒和行星輪3嚙合導致的。

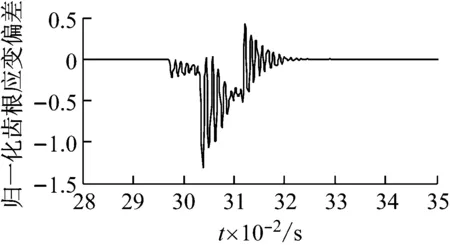
(a) 齒面剝落

(b) 輪齒缺損

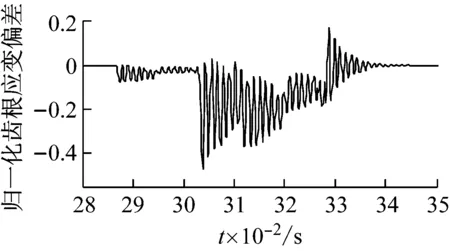
(c) 裂紋

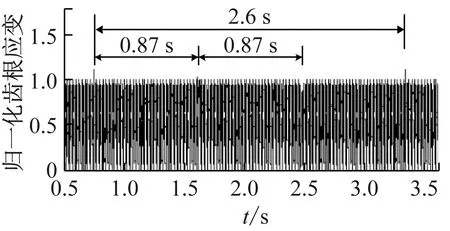
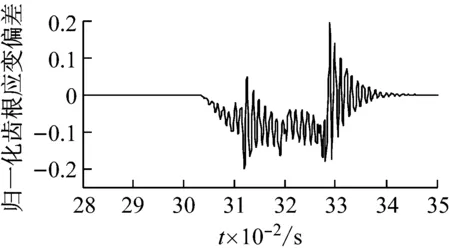
圖14 內齒圈故障時內齒圈的齒根應變信號

圖15所示為在三種故障下，當內齒圈故障齒與行星輪2發生嚙合時，內齒圈齒根應變信號的偏差。由圖15可知，不同內齒圈故障對內齒圈齒根應變信號的影響不同，每種故障所對應的齒根應變偏差與相應的時變嚙合剛度有一定的相關性，所以可以根據內齒圈齒根應變偏差的形式判斷不同內齒圈故障的類型。

(a) 齒面剝落

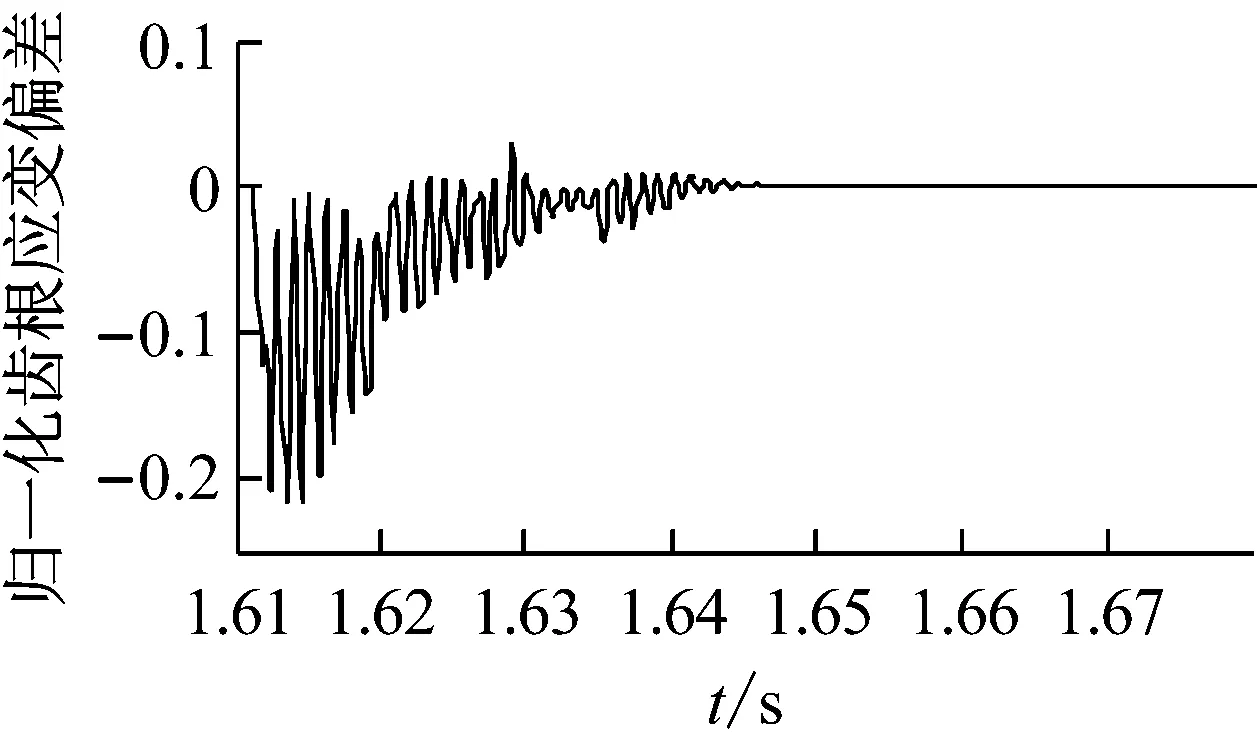
(b) 輪齒缺損

(c) 裂紋

對于內齒圈故障，當故障劇烈程度不同時，內齒圈齒根應變信號的表現與行星輪、太陽輪故障具有相同的規律，在此不再詳述。

5 結 論

本文研究了行星齒輪箱典型故障對內齒圈齒根應變的影響，得到以下結論：

(1) 行星齒輪箱中太陽輪、行星輪、內齒圈的故障均可以引起內齒圈齒根應變的變化。

(2) 當行星齒輪箱出現故障時，內齒圈齒根應變信號中會出現與故障有關的頻率成分：行星輪局部故障的頻率為行星輪的自轉頻率，太陽輪局部故障的頻率為太陽輪相對于行星架的旋轉頻率，內齒圈局部故障的頻率為行星架的旋轉頻率。

(3) 不同類型的故障對內齒圈齒根應變信號的影響不同，每種故障下的內齒圈齒根應變的形式與相應的嚙合剛度形式相關。

(4) 故障越劇烈，相應的內齒圈齒根應變偏差的能量水平越高。

通過以上結論可以發現，內齒圈齒根應變中包含有豐富的故障信息，是一種優質的故障特征載體信號，基于內齒圈齒根應變信號的行星齒輪箱故障診斷方法在理論上是可行的。

[1] PARKER R G, LIN J. Mesh phasing relationships in planetary and epicyclic gear[C]∥ASME 2003 design engineering technical conference and computers and information in engineering conference. Chicago: Journal of Mechanical Design, 2003.

[2] 雷亞國，湯偉，孔德同，等. 基于傳動機理分析的行星齒輪箱振動信號仿真及其故障診斷[J]. 機械工程學報, 2014, 50(17): 61-68.

LEI Yaguo, TANG Wei, KONG Detong, et al. Vibration signal simulation and fault diagnosis of planetary gearboxes based on transmission mechanism analysis[J]. Journal of Mechanical Engineering, 2014, 50(17): 61-68.

[3] INALPOLAT M, KAHRAMAN A. A theoretical and experimental investigation of modulation sidebands of planetary gear sets[J]. Journal of Sound and Vibration, 2009, 323(3/4/5): 677-696.

[4] FENG Z, ZUO M. Vibration signal models for fault diagnosis of planetary gearboxes[J]. Journal of Sound and Vibration, 2012, 331(22): 4919-4939.

[5] 馮志鵬，趙鐳鐳，褚福磊. 行星齒輪箱故障診斷的幅值解調分析方法[J]. 中國電機工程學報, 2013, 33(8): 107-111.

FENG Zhipeng, ZHAO Leilei, CHU Fulei. Amplitude demodulation analysis for fault diagnosis of planetary gearboxes[J]. Proceedings of the CSEE, 2013, 33(8): 107-111.

[6] 馮志鵬，褚福磊. 行星齒輪箱故障診斷的頻率解調分析方法[J]. 中國電機工程學報, 2013, 33(11): 112-117.

FENG Zhipeng, CHU Fulei. Frequency demodulation analysis method for fault diagnosis of planetary gearboxes[J]. Proceedings of the CSEE, 2013, 33(11): 112-117.

[7] 馮志鵬，范寅夕，LIANG Ming，等.行星齒輪箱故障診斷的非平穩振動信號分析方法[J]. 中國電機工程學報, 2013, 33(17): 105-110.

FENG Zhipeng, FAN Yinxi, LIANG Ming, et al. A nonstationary vibration signal analysis method for fault diagnosis of planetary gearboxes[J]. Proceedings of the CSEE, 2013, 33(17): 105-110.

[8] 張小棟，謝思瑩，牛杭，等. 光纖動態檢測技術的研究與進展[J]. 振動、測試與診斷, 2015, 35(3):409-416.

ZHANG Xiaodong, XIE Siying, NIU Hang, et al. Research on dynamic measurement technology of fiber optic sensors and their development[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(3): 409-416.

[9] NIU H, ZHANG X. Design on a bending stress measurement system of micro-gear with fiber Bragg grating[C]∥IEEE 10th International Conference on Nano/Micro Engineered and Molecular Systems (NEMS). Xi’an:[s.n.], 2015.

[10] ZHAO X, NIU H, ZHANG X. Research on measurement for bending stress of gear with fiber Bragg grating (FBG) and optimization of FBG probe installation[C]∥IEEE 12th International conference on Ubiquitous Robots and Ambient Intelligence (URAI). Goyang:[s.n.], 2015.

[11] SANCHEZ M B, PEDRERO J I, PLEGUEZUELOS M. Critical stress and load conditions for bending calculations of involute spur and helical gears[J]. International Journal of Fatigue, 2013, 48(4):28-38.

[12] 靳廣虎，朱如鵬，李政民卿，等. 齒寬系數對面齒輪齒根彎曲應力的影響[J]. 中南大學學報(自然科學版), 2011, 42(5):1303-1309.

JIN Guanghu, ZHU Rupeng, LI Zhengminqing, et al. Impact of coefficient of tooth width on bending stress of face gear[J]. Journal of Central South University (Natural Science), 2011, 42(5): 1303-1309.

[13] 孫智民，季林紅，沈允文. 2K-H行星齒輪傳動非線性動力學[J]. 清華大學學報(自然科學版), 2003, 43(5): 636-639.

SUN Zhimin, JI Linhong, SHEN Yunwen. Nonlinear dynamics of 2K-H planetary gear train[J]. Journal of Tsinghua University (Natural Science), 2003, 43(5): 636-639.

[14] 程哲，胡蔦慶，馮占輝，等. 基于動力學仿真的行星輪系損傷檢測方法[J]. 振動、測試與診斷, 2010, 30(4): 379-383.

CHENG Zhe, HU Niaoqing, FENG Zhanhui, et al. Detection of damage in planetary gear sets based on dynamical simulation[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(4): 379-383.

[15] 李同杰，朱如鵬，鮑和云，等. 行星齒輪系扭轉非線性振動建模與運動分岔特性研究[J]. 機械工程學報,2011,47(21): 76-83.

LI Tongjie, ZHU Rupeng, BAO Heyun, et al. Nonlinear torsional vibration modeling and bifurcation characteristic study of a planetary gear train[J]. Journal of Mechanical Engineering, 2011, 47(21): 76-83.

[16] Calculation of load capacity of spur and helical gears-part 3: calculation of tooth bending strength: ISO 6336-3—2006[S]. Switzerland: International Organization for Stand-ardization, 2006.

[17] SANCHEZ M B, PLEGUEZUELOS M, PEDRERO J I. Calculation of tooth bending strength and surface durability of internal spur gear drives[J]. Mechanism and Machine Theory, 2016, 95:102-113.

[18] CHAARI F, FAKHFAKH T, HADDAR M. Dynamic analysis of a planetary gear failure caused by tooth pitting and cracking[J]. Journal of Failure Analysis & Prevention, 2006, 6(2):73-78.

[19] 萬國志，訾艷陽，曹宏瑞，等. 時變嚙合剛度算法修正與齒根裂紋動力學建模[J]. 機械工程學報，2013, 49(11): 153-160.

WAN Guozhi, ZI Yanyang, CAO Hongrui, et al. Time-varying mesh stiffness algorithm correction and tooth crack dynamic modeling[J]. Journal of Mechanical Engineering, 2013, 49(11): 153-160.

[20] 楊軍，張浬萍. 風電行星齒輪系統變載荷激勵動力學模型及其響應特性[J]. 中國機械工程, 2013, 24(13): 1783-1788.

YANG Jun, ZHANG Liping. Varying load incentive dynamics model and response characteristic of planetary gear system of wind turbine[J]. China Mechanical Engineering, 2013, 24(13): 1783-178.

Action mechanism of planetary gearbox’s typical faults on tooth root strain of ring gear

NIU Hang2, ZHANG Xiaodong1，2, ZHAO Xindan2, HOU Chenggang2

(1. Key Laboratory of Education Ministry for Modern Design and Rotor-Bearing System, Xi’an Jiaotong University, Xi’an 710049, China;2. School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

Planetary gearboxes have lots of advantages and are widely used in mechanical transmission systems of many fields. However, severe work conditions result in many failures of planetary gearboxes, so it is necessary to develop their fault diagnosis methods. Traditional fault diagnosis methods of planetary gearboxes based on vibration signals have limitations to identify their early and weak faults, so a new fault diagnosis method based on their ring gears’tooth root strain signals was proposed and the action mechanism of planetary gearbox’s typical faults on their tooth root strain of ring gear was discussed here. Firstly, the modeling method of the tooth root strain of ring gear was analyzed, and the model of the tooth root strain of ring gear was decomposed into the planetary wheelring gear meshing force model, the ring gear tooth form coefficient model and the load between teeth sharing coefficient model. Secondly, the planetary wheelring gear meshing force was calculated with the torsional model of planetary gearboxes, the ring gear tooth form coefficient was derived with the mechanics of materials, and the load between teeth sharing coefficeient of internal meshing was analyzed. Finally, the effects of the faults of planetary gearboxes on the meshing stiffness were studied, and the variation laws of tooth root strain of ring gear under typical faults were computed with the model of the toothroot strain of ring gear. The modeling simulation results showed that faults of different types, different positions and different intensities have different influences on the tooth root strain signals of ring gear and the proposed fault diagnosis method of planetary gearboxes based on tooth root strain is feasible theoretically.

planetary gearbox; ring gear; tooth root strain; vibration; fault diagnosis

國家自然科學基金(51675419)

2016-01-08 修改稿收到日期：2016-03-05

牛杭 男，博士，1991年生

侯成剛 男，博士，副教授，1968年生

TH132.41; TH17

A

10.13465/j.cnki.jvs.2017.09.037