挖掘機機械臂軌跡規劃分析

摘 要：規劃機械臂軌跡，是控制機械臂的基礎和前提，主要目的是通過規劃機械臂運動速度、加速度、脈動和角度等，從而確保機械臂能夠穩定、平滑的運動。其次，規劃機械臂的軌跡，也能夠防止其在運行時出現沖擊振動，從而將機械臂的可靠性和工作效率提升，在分析挖掘機運動過程及結構的前提下，通過標準的D-H法，將相應的研究模型構建起來，并且，在運動學理論基礎上，進行相應的分析，那么，通過文章下文對挖掘機機械臂軌跡規劃的相關內容進行了分析論述，從而為有關單位及工作人員在實際工作中提供一定的幫助作用。

關鍵詞：挖掘機；機械臂；軌跡規劃

DOI：10.16640/j.cnki.37-1222/t.2017.09.124

挖掘是用途廣泛、功能特殊的工程機械設備之一，在交通運輸工程、民用建筑、水利水電和礦業開采等工程中都發揮重要作用。近年來，我國地質災害頻發，而在事故救援搶險中，作為重要的救災設備，挖掘機充分的體現出了自身的價值。然而隨著施工環境的日益復雜，事故災害的嚴重性，對挖掘機的工作精度和性能方面也提出了全新的要求。其中挖掘機機械臂軌跡的規劃就屬于研究的重點。因此，文章通過下文圍繞有關方面的內容進行了詳細的分析和論述。

1 研究背景分析

進入21世紀以來，我國社會經濟發展速度不斷加快，為了更好的服務于人類，對挖掘機設備的作業質量也提出了全新的要求，怎樣完善其工作可靠性及工作效率已經成為當前的工作重點。而合理的規劃挖掘機的軌跡，令其可以平穩、快速的將挖掘任務完成，就可以將挖掘機工作中所遇到的問題解決掉，從而將挖掘機的整體性能提升。所以，怎樣能夠更好的完善其運行軌跡，成為了處理問題的重點。

在工作中，機械臂的速度、加速度和位移等問題是軌跡規劃研究的主要內容。它主要利用對軌跡的控制確保末端可以有效運行和工作。規劃機械臂軌跡，是逆運動學問題與機械臂正常運動學問題的具體應用，機械臂的動態性能和規劃的合理性之間聯系密切。所以，在機器人學中，軌跡規劃已經成為了一個重要的研究領域和熱點。所以，規劃機械臂軌跡，一定要采取合適的措施和遵循一定的原則，防止其速度、加速度和位移的突然變化，確保其能夠連續運動，從而將運動期間的振動與沖擊波減少。因此，這就規定我們對軌跡規劃的相關問題要更加深入的進行研究和分析，不斷強化和完善現存的機器人技術，更好的滿足實際應用需求，更好的服務于人類。

機械臂最優運動規劃的內涵：在將機械臂的始末位置條件給出來后，從而將一條最優的關節運動軌跡給出來。其中，可以參考很多方面優化機器人軌跡規劃算法的性能，例如，系統最優和時間最優。那么，為了將機械臂作業單元生產效率提升到一個更高的檔次，所以需要研究好以時間最優為目標的軌跡規劃問題，其中，可以從以下兩個方面研究分析機械臂最優時間軌跡規劃問題：首先，在時間最優化目標基礎上，順著規定的路徑研究連續路徑問題；其次，在最優化時間基礎上，對點到點的運動最優化處理方案制定出來。

2 挖掘的基本構造及位姿描述

下圖是文章研究的主要挖掘機類型，有鏟斗、斗桿、動臂和底座一同構成了該挖掘機。文章在對挖掘機軌跡規劃內容進行研究時，沒有固定其底座，只在一個平面內運動挖掘機，因此，要對兩個自由度進行分析和考慮。

關節的運動情況會在某種程度上影響到機械臂末端執行器的位姿，所以，在分析運動學時，需要將一個指定的參考坐標系為各個關節制定出來。在分析機械臂運動學時，在需要對兩個坐標系之間的位姿關系進行描述時，可以利用變換矩陣的方式，用一個坐標系描述分析另一個坐標系。

在上個世紀五十年代，有Hartenberg和Denavit提出了D-H法，然后建模和表示機械臂。此種方法主要是利用推導坐標系之間的變換矩陣將坐標系之間的關系表示出來，在確定出來坐標系之間的關系以后，可以將運動學方程構建起來。

有平移關節或者旋轉關節連接鋼體連桿一同構成了機械臂，在編號處理連接桿時，依據從低到高或者從底座底部到末端執行器的方法完成標號處理，0為固定的底座標桿，1是和其相連接的標桿，1為二者之間的關節編號；另一端用連桿2與其連接，然后2是兩者之間的連接關節，然后，依據這樣的方式依次列出。

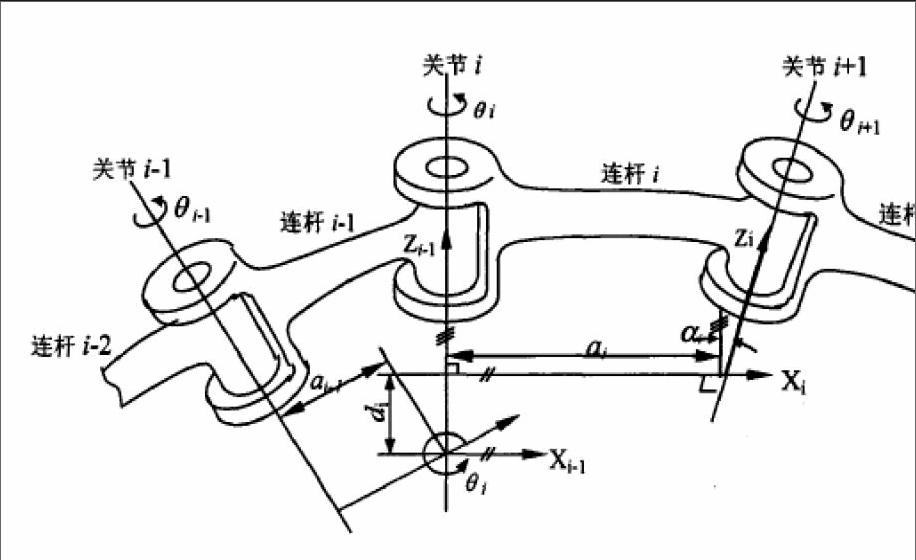
在連桿坐標系內對一個連桿進行藐描述時，通常要用兩個參數來完成，分別是與a1所在平面垂直的夾角a1和公共法線的距離a1；而在對相鄰連桿關系進行描述時，可能會應用到其他的參數，兩連接桿法線的夾角和兩個連桿的相對位置d1。其中，D-H參數即為這個四個參數的合稱。

首先，a1即為連桿的長度，它主要是指關節i+1和關節i之間的公垂線之間的距離。其次，關節i+1和關節i之間的夾角即為連桿扭角；連桿的位置；除最后一個或者第一個連桿之外，通過關節i連接兩個相鄰的連桿，所以，有兩條公法線會與關節軸線i相垂直。其中，連桿偏移量就是這兩條公法線之間的距離；可以用d1進行表示。關節i相鄰兩個公垂線的夾角即為關節角。

就轉動關節而言，有個變量的的關節角存在于四個參數中，剩余的參數只是和連桿的屬性有關，屬于一個常數；就平動關節而言，連桿偏移量在四個參數中屬于變量，剩余的參數都是常數。具體的模型圖如下所示：

在D-H表示法中，n個關節需要將n+1個坐標系構建起來，用Ooxoyozo表示參考坐標系。文章中所研究的挖掘機主要運動于鉛面之內，三個關節的z軸是互相平行的，并且與鉛面相互垂直，所以，在這種特殊的情況下，連桿的扭角a和連桿偏移量都是0，也就是在此基礎上構建的挖掘機坐標系統。

3 挖掘機機械臂軌跡規劃研究

3.1 設計關節軌跡和機械臂軌跡

在規劃軌跡時，對運動的中間過程不予以考慮，點到點的處理運動期間特定中間點位置中所出現的問題。在點到點的運行期間，在笛卡爾空間內是難以有效規劃機械末端的執行器運動路徑，所以，對機械臂的各個關節只需在關節空間中進行規劃即可，而在確定了關節空間軌跡后，也就隨之確定出了笛卡爾空間的運動軌跡。

3.2 軌跡函數的確定

關節軌跡的規劃即為機械臂軌跡規劃，獲取時間與關節角度之間的 映射關系是規劃關節軌跡的主要目的，其中，按照機械臂末端軌跡的位置確定出起止時刻的角度。然而，在規劃關節時，只對兩點之間角度的變化進行考慮還遠遠不夠，因為會有很多的變數存在于關節軌跡中。

在規劃機械臂軌跡時，單純的只是分析和考慮角度的連續性，將軌跡用線性函數表示出來，這樣就需要用常數表示關節速度，用0表示加速度，此種情況會誘發速度突然變化等不合理情況，這樣，就會有振動問題出現在機械臂中。確保運動的平穩性是規劃軌跡的基本要求之一。所以，在規劃期間，必須要確保有一定能的連續性存在于規劃時所選取的描述運動軌跡函數中，并且，還要求有一定的連續性存在于它的一階和二階導數中。在此前提下，規劃機械臂關節時，主要從以下幾點入手：

規劃關節的角度；規劃關節的速度；規劃關節的加速度；規劃關節的脈動。

在規劃關節時，就是分別用時間函數將上述四個方面表示出來，按照規劃的函數，依據時間段控制各個環節，最后確保執行機構將給定的目標確定出來。

3.3 依據解析法規劃機械臂軌跡

首先，分析軌跡函數的已知條件。將式子中各個項目的系數通過軌跡規劃確定出來，然后向所得到的速度、脈動曲線、角度和加速度之間帶入所求出的各個系數。各個曲線都可以滿足對應的約束條件。然而，對系數進行求解時，假設運動期間有較多的中間點，各個點位置的加速度和速度都是連續的。

3.4 在優化算法基礎上，規劃機械臂軌跡

在實際工程中，機械臂因為受到力矩大小、機械機構等條件的制約，其加速度、脈動和速度都不可能無限增長。通過分析可知，在h1，h2...hn-1，控制任意給定時間間隔點時，能夠將各個關節的軌跡求解出來。然而，這種情況下所求出的加速度、脈動和速度之間的軌跡可能難以滿足機械臂本身的約束條件，函數曲線的最大值可能將原始的約束范圍超出，因此，在規劃軌跡時，按照以上間隔時間進行分析是不合理的。

為了確保所規劃的機械臂軌跡可以滿足具體運行的約束條件，它應該通過優化方法優化時間間隔點，這樣，在確保機械臂軌跡最大值不將約束范圍超出的基礎上，對運動時間進行優化處理，從而有效的優化運動軌跡。

而在優化時間間隔時，可以通過智能化或者解析方法進行優化處理。然而，因為存在的約束條件較多，迭代過程十分復雜繁瑣，計算較難。考慮到實際軌跡規劃問題，主要就是優化處理函數表達式的參數，而在對函數優化問題進行處理時，需要應用一些智能化的方法。所以，在規劃機械臂軌跡時，將智能化的方法應用進去，可以大大提升優化效率。

在智能型優化方法中，需要評價個體的優劣情況。而在評價個體時，所以，需要將某個方面作為評判依據，所以，此評判依據被稱之為適應性函數。在規劃機械臂軌跡時，需要將一個適應值函數構建起來，進而在此基礎上評判軌跡的優劣情況。所以，選擇一個具有代表意義、合理性的函數構建軌跡關系意義非常重大。

3.5 基于時間最優化的約束條件和優化目標

就挖掘機工業而言，生產效率會在某種程度上決定著其運動速度，那么，為了能夠將挖掘機效率提升到一個更高的檔次，所以，需要不斷優化其運動時間，越短越好。而在求解軌跡函數表達式時，除了要按照運動學約束條件構建各個環節軌跡外，需要努力降低總的運動時間。與此同時，在優化處的時間需要展開軌跡優化時，一定要確保在一定的約束范圍內控制軌跡的加速度、脈動曲線和速度，不然，難以將有效的時間優化出來，所以，就需要再次規劃軌跡。

在優化多個關節的機械臂軌跡時，可以通過兩種方法進行求解分析：首先，單獨優化各個關節，并且，需要彼此獨立各個關節的優化過程，求解過程簡單是這種方法的主要特征。然而，因為各個關節有著不盡相同的動作時間，動作連續性不到位，因此，控制起來比較困難；其次，在一同優化所有關節時，求解過程較為復雜是這種方法的主要特征，然而，各個關節有著相同的運動時間，動作控制程序簡單，動作連續性優越。因為，對控制的難易性需要進行考慮，所以，要采取時間最優法進行控制。

研究發現，通過以上策略將各個關節的約束條件表示出來后，優化的適應值函數用總運動時間表示出來，然后將求出最優解。

在尋找最優解時，可以把約束條件當作判斷依據進行應用。一旦粒子搜索到的解可以滿足相應的約束條件，這樣，在將適應值計算出來后，在進行迭代處理。如果粒子所搜出的解同約束條件不相符，這樣所設置出的適應值為一個較大的數。但是，這種方法也存在一定的不足之處，也就是它需要一次判斷約束條件，在尋找最優解時，會耗費掉很多的時間。在情況比較搞特殊的時候，難以將滿足條件的最優解找出來。

4 結語

當前，在很多工程中都廣泛的應用了挖掘機設備，然而，隨著工程復雜度的提升，人們也將越來越高的要求了挖掘機作業的質量。傳統的挖掘機設備中，一些問題逐漸表現出來，為了能夠更好的滿足生產、生活的需要，需要將智能化的技術應用到挖掘機機械臂軌跡規劃中，從而為提升挖掘機設備的運作質量而打下基礎。而對挖掘機軌跡的合理優化，是實現挖掘機智能化、自動化覺得基礎和前提，也是提升挖掘機工作質量和效率的重要保證。

參考文獻：

[1]王國明，馬履中.基于SimMechanics的二自由度并聯機器人運動學仿真[J].機械設計與制造，2012（06）：623-624.

華僑大學研究生科研創新能力培養計劃資助項目

作者簡介：鐘星（1992-），女，江西宜春人，在讀碩士研究生，研究方向：智能控制技術及自動化裝置。