從教材實例談如何理解教材教學(xué)
管明貴
[摘 要] 用教材教是數(shù)學(xué)教學(xué)的基本準(zhǔn)則,但如何教卻因人而異. 不少教師在常態(tài)課教學(xué)中并沒有真正領(lǐng)會用教材教的含義,使得學(xué)生陷入數(shù)學(xué)學(xué)習(xí)的一種惡性循環(huán)之中. 筆者結(jié)合自己的實踐經(jīng)驗以為,腳踏實地地研究教材,思考為什么這么教,理解教材選擇例題的重要性,才是一個教師真正成長的標(biāo)記.
[關(guān)鍵詞] 教材教學(xué);數(shù)學(xué);函數(shù);素養(yǎng);建模;圖像
從小學(xué)數(shù)學(xué)到初中數(shù)學(xué),我們發(fā)現(xiàn)學(xué)生學(xué)習(xí)數(shù)學(xué)的興趣驟然下降. 這是由很多原因造成的,比如:初中數(shù)學(xué)需要對數(shù)學(xué)知識本質(zhì)屬性更進一步的認識,這勢必導(dǎo)致數(shù)學(xué)學(xué)習(xí)變得相對枯燥;種種升學(xué)應(yīng)試造成的壓力,讓教師在教學(xué)中不敢放手讓學(xué)生還原知識來源的過程,建構(gòu)新知的形成途徑,要讓學(xué)生短時間內(nèi)快速理解知識、掌握知識,還不如通過大量的試題訓(xùn)練來得高效.
這些因素造成初中生數(shù)學(xué)學(xué)習(xí)出現(xiàn)了下列問題:其一,對新知一知半解,通過大量訓(xùn)練來理解新知、運用新知,離開了這種訓(xùn)練模式,學(xué)生就不會學(xué)習(xí)數(shù)學(xué)、不會思考問題;其二,這種訓(xùn)練模式下的數(shù)學(xué)學(xué)習(xí)讓學(xué)生接觸的是機械化的操作,對于熟練的問題模型尚等得到分數(shù),但面對以靈活考查能力為主的試題則無從下手;再者,最關(guān)鍵的是學(xué)生對學(xué)習(xí)數(shù)學(xué)的興趣已經(jīng)完全被扼殺了,如今初中生喜歡數(shù)學(xué)的愈來愈少. 中科大研究所調(diào)查顯示,若數(shù)學(xué)競賽對升學(xué)不具備加分作用,百分之九十九的學(xué)生都是不喜歡數(shù)學(xué)競賽的.
這也從一個側(cè)面反映了初中數(shù)學(xué)教學(xué)陷入了模式化過渡的教學(xué)之中. 西南師大陳重穆教授說:形式化是數(shù)學(xué)的特征之一,模式是數(shù)學(xué)問題的經(jīng)典總結(jié),在恰當(dāng)?shù)姆秶鷥?nèi)運用非形式化手段以及模式識別,對于學(xué)生學(xué)習(xí)數(shù)學(xué)是高效的途徑. 但是,現(xiàn)在初中數(shù)學(xué)教學(xué)陷入了一種模式化過渡的誤區(qū),即合理的新知教學(xué)也演變成三分之一的新知教學(xué),三分之二的知識訓(xùn)練,這種做法對于學(xué)生的數(shù)學(xué)興趣和創(chuàng)新性是無益的.
課程標(biāo)準(zhǔn)中明確指出:數(shù)學(xué)教學(xué)旨在培養(yǎng)學(xué)生的抽象能力、運算能力、數(shù)學(xué)建模、數(shù)據(jù)分析等素養(yǎng),通過數(shù)學(xué)知識理解其運用于生活、作用于生活的目的. 如何將教材中的知識做合適于學(xué)情的開發(fā),并在教學(xué)中進行演繹才是用教材教最好的反饋.
本文以八年級函數(shù)一節(jié)中一個問題為例,通過教材設(shè)計思路研究、教材知識結(jié)構(gòu)研究、教材教學(xué)價值研究、學(xué)生的認知結(jié)構(gòu)分析等方面來談?wù)勅绾斡媒滩慕?
問題情境
蘇教版八年級“5.1 函數(shù)”一節(jié)中的問題:小麗、小明、小亮乘車去旅游.
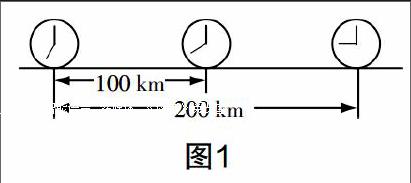
如圖1,汽車在公路上勻速行駛,用t來表示汽車行駛的時間,s表示汽車行駛的路程. 怎樣表示s與t的關(guān)系?
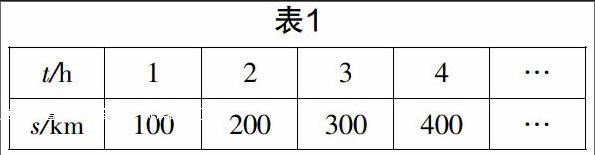
可以列表表示(如表1):
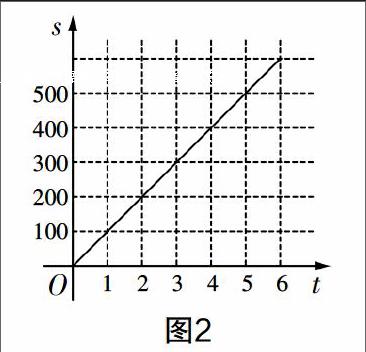
可以在坐標(biāo)系中畫圖表示(如圖2):
可以列式表示:因為汽車勻速行駛的速度為100 km/h,所以s=100t.
提出問題:變量s是變量t的函數(shù)嗎?為什么?
通常,表示兩個變量之間的關(guān)系可以用3種方法:表格、圖形和數(shù)學(xué)式子. 表示兩個變量之間的式子通常稱為函數(shù)關(guān)系式,例如s=100t就稱為s與t的函數(shù)關(guān)系式.
教材知識結(jié)構(gòu)分析
教材中對于函數(shù)的學(xué)習(xí)采用了以生活情境為載體的設(shè)計,首先讓學(xué)生明白要學(xué)習(xí)的函數(shù)來源生活,是對生活問題的抽象、是對生活問題本質(zhì)屬性的研究;其次,教材給出了函數(shù)表示的三種方法(即列表法、圖像法、解析式法,這是函數(shù)表示的核心知識),并從函數(shù)圖像和函數(shù)關(guān)系式中理解函數(shù)是一種變量與變量之間的關(guān)系,多維度、多層次、多方面地接觸函數(shù)概念以及函數(shù)的意義和本質(zhì)屬性. 讓學(xué)生從本情境中感知事物變化的過程以及變量主導(dǎo)的相互關(guān)系式,并引導(dǎo)學(xué)生思考生活中還有很多問題都具備類似的變量性,因此變量研究是普適性的,成為后續(xù)學(xué)習(xí)的核心. 要將這些變量關(guān)系表述出來,該如何利用情境問題中的三種表示方法進行滲透,這成為后續(xù)揭示事物變量關(guān)系規(guī)律的核心手段.
教材設(shè)計思路分析
對于用教材教,教師還需要深刻理解教材為什么這樣設(shè)計. 可以從三個方面分析:
(1)我們回到問題情境,學(xué)生從問題中比較容易理解:在速度為定值的情況下,路程和時間成一定的變量關(guān)系,這是啟發(fā)變量思維形成函數(shù)概念的一個關(guān)鍵節(jié)點.
(2)表格的作用在于將這種變量關(guān)系的展示直觀化、具象化,使學(xué)生明確這種變量關(guān)系的直觀性. 同時表格還可以清晰地展示變量之間的聯(lián)系,即速度是定值,這種以圖表形式表達變量關(guān)系的方式是函數(shù)表達的重要手段,但是時間t的選擇往往以整數(shù)形式較為方便,暗示了以表格方式表達變量關(guān)系的局限性.
(3)圖像是變量關(guān)系最直觀的體現(xiàn),教材以圖形展示位移和時間的關(guān)系,其設(shè)計明顯有兩個用意:其一是了解圖像是表示變量關(guān)系的主要手段,從圖像變換中理解不同變量模型具備不同的圖像變換;其二是圖形化讓變量關(guān)系的研究成為一種直覺,即數(shù)形結(jié)合思想在函數(shù)學(xué)習(xí)中的不斷滲透.
從教材給出的問題,我們清晰地掌握了其基本教學(xué)意圖:掌握變量關(guān)系的三種表示方法,即列表法、圖像法、解析法,這是函數(shù)表示的基本構(gòu)成;從情境問題中理解特殊到一般研究方法的重要性,數(shù)形結(jié)合思想貫穿始終.
教材的教學(xué)價值分析
函數(shù)是中學(xué)數(shù)學(xué)最重要、最核心的數(shù)學(xué)概念,教材的問題設(shè)計正是基于這樣的考慮. 教師要學(xué)會理解和體會教材中問題的價值,才能理解為什么要用教材教.
1. 引入問題的主要目的是向?qū)W生滲透變量間關(guān)系的三種表示方法,這為學(xué)生后續(xù)研究類似問題、理解生活中普遍存在的函數(shù)關(guān)系奠定了研究基調(diào),即圖像法和列表法可以直觀地研究變量關(guān)系,解析式法可以將這種關(guān)系數(shù)學(xué)化,這是教學(xué)價值一.
2. 在以往中學(xué)數(shù)學(xué)雙基的基礎(chǔ)上,初中數(shù)學(xué)又強調(diào)了基本活動經(jīng)驗和基本數(shù)學(xué)思想,教材問題的教學(xué)價值二恰好在此處體現(xiàn)出來. 基本活動經(jīng)驗體現(xiàn)了本問題的數(shù)學(xué)現(xiàn)實之用,基本數(shù)學(xué)思想可以從特殊到一般、數(shù)形結(jié)合思想上得到體現(xiàn).
3. 價值三也是教材最想告誡教師在教學(xué)中應(yīng)該關(guān)注的一點:學(xué)習(xí)數(shù)學(xué)最主要的目的是什么?是為生活、生產(chǎn)實際服務(wù). 在看不到數(shù)學(xué)的地方,找到數(shù)學(xué)知識的運用和價值,是教師需要向?qū)W生進行滲透的. 這種在建模中不斷“思考——抽象——再思考”的過程,是數(shù)學(xué)學(xué)習(xí)的重要方式.
學(xué)生認知結(jié)構(gòu)分析
1. 常量思維動態(tài)化
勒溫認為“學(xué)習(xí)即認知結(jié)構(gòu)的變化”. 可以這么說,學(xué)生對于路程和時間的關(guān)系,并不是老師想象的那樣屬于變量認知,勒溫研究表明學(xué)生只認識這是一種常量之間的聯(lián)系. 函數(shù)是研究變量與變量之間的關(guān)系,如何讓這樣的觀念在教學(xué)中滲透?這就需要考慮時間的任意性問題,當(dāng)在任意時刻計算路程,這種動態(tài)的關(guān)系自然而然地滲透到學(xué)生的頭腦中,變量關(guān)系的建立初具雛形.
2. 變量關(guān)系代數(shù)化本質(zhì)即方程
在“s=100t”中,速度100是已知的,S與t是未知的,這是一個含有兩個未知數(shù)的等式,也就是為了尋求未知數(shù),在已知數(shù)和未知數(shù)之間建立的一種等式關(guān)系. 在兩個未知數(shù)中,給出一個未知數(shù)的值,就可以求出另一個未知數(shù)的值,并且有無數(shù)組解,s與t的值是不可數(shù)的. s與t是在變化著的變量,一個變化能引起另一個變化,此時只是認識到有兩個變量,但對兩個變量有聯(lián)系以及聯(lián)系的程度認識還比較模糊.
3. 變量和變量之間的關(guān)系即核心——函數(shù)
“s=100t”,這不僅是路程、速度、時間之間的關(guān)系,這是同一運動系統(tǒng)中兩個變量之間有相互制約、相互協(xié)調(diào)的關(guān)系. 第一,發(fā)生變化的量稱為“變量”;第二,不發(fā)生變化的量稱為“常量”;第三,對于變量t的每一個值,s都有唯一的值與之對應(yīng),則稱t為自變量,s為t的函數(shù);第四,如果當(dāng)t=a時,s=b,那么稱b為t=a時的函數(shù)值. 至此,學(xué)生才對函數(shù)的概念有一個比較清楚的認識.
到這里,對本問題的剖析已經(jīng)全面到位. 通過深刻的理解和認知,教師認識到教材中的例題是精挑細選的,經(jīng)典的緣由是如何形成的. 作為教師,也進一步理解了用教材教學(xué)和用教輔教學(xué)的天壤之別. 教教材是課程標(biāo)準(zhǔn)積極提倡的,也是提高學(xué)生數(shù)學(xué)學(xué)習(xí)能力、思維能力、綜合素養(yǎng)的根本,更是教師自身專業(yè)化成長的訴求. 筆者以為,腳踏實地地研究教材,思考為什么這么教,理解教材選擇例題的重要性,才是一個教師真正成長的標(biāo)記. 張奠宙先生所說的“用心體會教教材,合理思考用教材教”正是這個含義吧!

