隨機振動條件下的橡膠襯套疲勞壽命預測＊

吳趙佳侯永平張建文

（1.同濟大學 新能源汽車工程中心，上海 201804；2.上海機動車檢測認證技術研究中心有限公司，上海 201805）

隨機振動條件下的橡膠襯套疲勞壽命預測＊

吳趙佳1侯永平1張建文2

（1.同濟大學 新能源汽車工程中心，上海 201804；2.上海機動車檢測認證技術研究中心有限公司，上海 201805）

本文通過試驗與有限元仿真相結合的方法，以等效最大主應變作為疲勞損傷參量建立了橡膠材料的疲勞壽命預測模型，采用Van Der Waals本構方程模擬橡膠材料的力學性能，在準確擬合橡膠襯套剛度特性的基礎上，對其在實際道路隨機振動條件下的壽命進行了預測。試驗結果表明，該方法能夠準確地預測出橡膠襯套在多軸載荷作用下的疲勞壽命。

1 前言

隨著汽車工業的發展，人們越來越注重汽車的NVH性能及其舒適性。汽車底盤中的橡膠襯套不僅具有連接各部件的作用，而且能夠減緩由底盤傳遞至車身的力和振動，是底盤中的重要組成部分[1]。襯套傳遞的力對車輛平順性和舒適性及高頻振動下的NVH特性有著很大影響，也直接影響到用戶實際用車的滿意度。為了預防橡膠襯套在用戶實際使用中出現失效問題，對橡膠襯套進行疲勞耐久性能的研究以及對橡膠襯套的疲勞壽命進行早期且有效的預測非常關鍵。

黃鵬程等人[2]基于橡膠材料的應變能密度—壽命曲線，準確地識別了潛在失效位置，并預測了受力狀態簡單的橡膠零件的疲勞壽命；王文濤等人[3]以車用變速器懸置與發動機后懸置為研究對象，利用張量形式的疲勞壽命預測公式預測了兩種懸置在單軸拉伸、簡單剪切兩種工況下的疲勞壽命。本文在以往研究的基礎上，以某車型前副車架上的橡膠襯套為例，結合臺架試驗與CAE仿真對橡膠襯套的耐久性能進行了深入研究。與以往的簡單載荷工況下的研究相比，更突出了與實際相結合的工程應用背景。

2 橡膠襯套疲勞壽命預測模型建立

為預測橡膠材料零件的疲勞壽命，目前主流的研究方法有裂紋成核壽命預測方法和裂紋擴展壽命預測方法[4]。本文采用裂紋成核壽命預測方法，該方法依據連續介質力學理論，主要考察材料某一點的應力或應變狀態的時間歷程，利用疲勞損傷理論得到材料產生特定的裂紋尺寸所需的載荷周期數來預測材料壽命。基于此方法需要做如下假設：一是橡膠材料符合各向同性；二是橡膠材料元件表面不存在可見裂紋。疲勞裂紋成核壽命預測方法需要尋找或構建一個疲勞損傷參量，然后建立起裂紋成核壽命與這些主要參量的聯系。

在橡膠襯套的實際使用過程中，受力狀態通常較為復雜。由于不同性質的載荷（剪切載荷、拉伸載荷及壓縮載荷）對橡膠材料的疲勞壽命影響不同[5]，因此，本文采用等效最大主應變作為疲勞損傷參量，從而能綜合考慮到不同性質的各種載荷，能夠與橡膠元件的疲勞壽命實際情況更吻合。等效最大主應變的計算式為：

式中，εf為等效應變；ε1、ε2和ε3為3個方向的主應變。

建立的疲勞壽命預測分析流程如圖1所示。

圖1 疲勞壽命預測分析流程

3 橡膠襯套有限元仿真

3.1 有限元建模與分析

橡膠材料與常見金屬材料的力學特性有所不同，在橡膠材料的形變過程中，應力－應變關系是非線性的。通常，使用應變勢能來表示橡膠類超彈性材料的特性。在仿真分析過程中，不同的本構方程對應著不同的應變勢能表達式[6]。一般情況下，在橡膠材料試驗數據充分的條件下，采用材料系數較多的本構模型（Ogden模型和Van Der Waals模型等）可以更準確地擬合試驗結果；而當試驗數據不足時，則需要采用材料系數較少的本構模型。為了使橡膠材料的本構模型更符合材料的實際特性，本文采用帶有4個材料參數的基于熱力學統計理論的Van Der Waals本構模型，其應變能函數為：

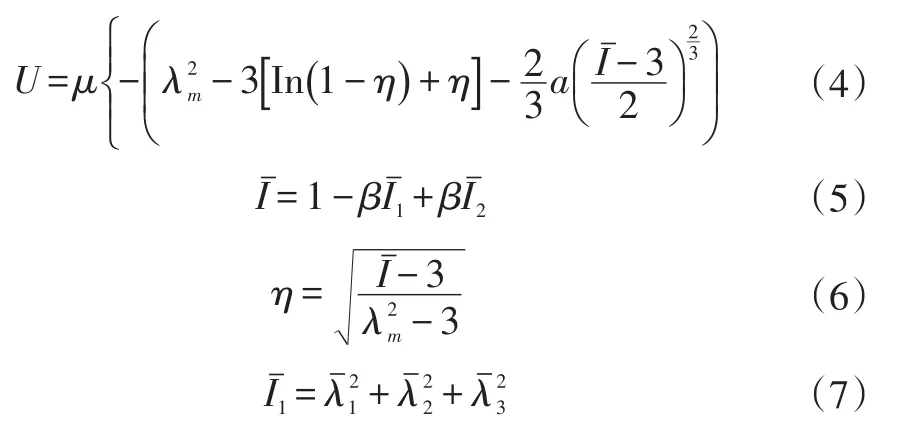
式中，U為應變能；μ、λm、a和β為材料系數；J為總體積比；λi為主伸長率。

研究所用的橡膠襯套由內、外圈金屬及中間橡膠部分組成，建立的有限元模型如圖2所示。金屬部分定義為C3D8實體單元，橡膠部分定義為C3D8H雜交單元，在圓心建立參考點RP1。內圈金屬的外表面與橡膠之間，以及外圈金屬的內表面與橡膠之間定義為tie綁定約束；定義內圈與參考點之間為剛體約束；定義橡膠的自接觸以及兩腰型孔的面面接觸的摩擦系數均為0.4。完全固定外圈金屬的外表面，并在參考點施加所需要的載荷。考慮到橡膠襯套的實際狀態，使用隱性求解方法模擬橡膠靜態特性，使用顯性求解方法模擬橡膠粘彈性動態特性。

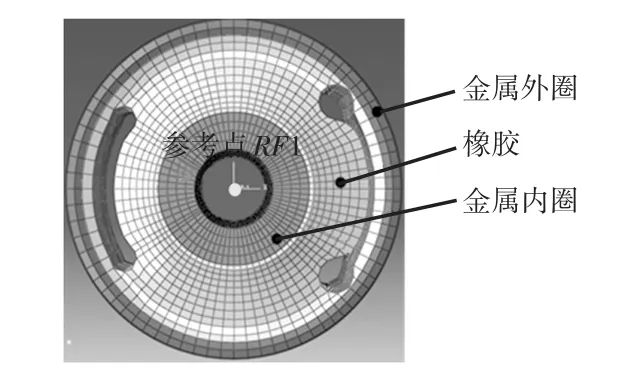
圖2 橡膠襯套有限元模型

3.2 輸入載荷獲取

無論是臺架試驗還是有限元仿真，邊界條件的確定都是一個極其關鍵的步驟。為了得到更為可靠的橡膠襯套疲勞壽命，必須提供盡可能符合實際的邊界條件，為此在疲勞試驗和仿真中的輸入信號采用襯套在實際工況下的載荷。

本文采用基于軸頭輸入的虛擬采譜方法獲取目標零件的響應載荷譜。利用該方法得到橡膠襯套處的載荷譜前，需要先建立多體動力學模型，在確保模型準確后才可進行仿真分析。選用ADAMS多體動力學仿真軟件，在ADAMS中，采用約束載荷加載法對車輪六分力進行載荷分解。在Car模塊中建立通用組件，包含的子系統有前橋、轉向、車身和車輪軸頭作動器，由于車輪六分力加載在軸頭，所以裝配中不包括輪胎和懸架試驗臺。在車輪作動器中可以加載三方向力、三方向扭矩和轉向盤轉角。載荷輸入采用通用驅動分析模塊，該模塊的加載方式與整車道路模擬試驗臺一致，由于研究對象橡膠襯套與前副車架相連，與車身之間沒有直接關聯，所以簡化為前橋總成加載方式，沒有加入后橋多體模型，并且車身相當于固定不動。加載信號文件為RPC格式，仿真頻率為250 Hz，載荷譜加載長度為205 s，選取減振器位移信號作為監控信號。

為了驗證多體動力學模型的準確性，需要對比仿真與實車試驗得到的左側減振器位移信號，仿真與試驗信號在時域上的趨勢對比如圖3所示，統計參數對比如表1所列。

圖3 左側減振器仿真與試驗的位移信號對比

表1 左側減振器仿真與試驗的位移統計參數對比 mm

由圖3和表1可看出，仿真結果與試驗結果有較高的一致性，即建立的多體模型與實車狀態較吻合，能夠用于計算仿真與試驗的輸入信號。將仿真計算得到的橡膠襯套處的力信號和擺角信號進行壓縮強化后，就可以得到疲勞試驗和仿真的輸入信號，輸入信號的雨流統計圖如圖4所示。

3.3 有限元分析結果

分別對橡膠襯套模型施加徑向空心側、徑向實心側和軸向3個方向的力，通過有限元仿真計算后便可得到襯套的剛度特性。將仿真得到的橡膠襯套力位移曲線與在MTS831彈性試驗機上實際測得的剛度作對比，對比結果如圖5所示，圖5中的虛線為設計要求的范圍。由圖5可看出，仿真與試驗的剛度均能達到設計的要求，說明該有限元模型可以準確地表征橡膠襯套的物理特性，可用于進一步的仿真模擬。得到準確的有限元模型后，便可進行橡膠襯套的疲勞耐久性分析。

4 橡膠襯套的耐久性分析

4.1 橡膠襯套的等效最大主應變—壽命曲線

為了得到橡膠襯套的疲勞屬性，采用啞鈴型試片做疲勞試驗，結合有限元仿真，可以得到等效最大主應變與壽命曲線。試驗時環境溫度為25℃，試驗中采用正弦位移加載，加載頻率為10 Hz。隨著循環數的增加，加載的最大載荷會突然降低，當最大載荷降低20%時，定義為橡膠失效。通過在不同的加載振幅下對試片分別進行耐久性試驗，可獲得加載位移與橡膠試片的壽命關系。結合有限元仿真得到的材料等效最大主應變與加載位移的關系，就能獲得等效最大主應變與試片壽命的數據關系。再使用最小二乘法進行擬合處理，則疲勞壽命與等效最大主應變的關系為：

式中，ε是橡膠試片的等效最大主應變；N是橡膠試片的壽命。

圖4 輸入信號雨流統計圖

圖5 仿真與試驗剛度對比結果

4.2 橡膠襯套應變時間歷程

應用虛擬試驗技術實現對轎車底盤目標零部件的疲勞壽命預估，需要獲得其在動態載荷作用下的應力/應變狀態，即應力/應變場時間歷程函數。對橡膠襯套來說，需要獲取關鍵點的等效最大主應變時間歷程。由于橡膠襯套的非線性，傳統金屬件獲取應力時間歷程的方法不再適用。因此，本文在計算得到在各種載荷工況下等效最大主應變與加載力和擺角的關系的前提下，再利用差值法建立三者之間的關系。圖6為在不同擺角下最大等效主應變與加載力的關系，圖7為在不同加載力下最大等效主應變與擺角的關系。

由圖可看出，當加載力保持不變的情況下，等效最大主應變與加載的擺角幾乎呈線性關系；在擺角不變的情況下，等效最大主應變隨加載力的增加而增大，但增長的斜率減小，這是因為橡膠材料具有非線性，會隨著加載力的增加而位移增量逐漸變小，因此，應變的增量也隨之減小。圖8是應變與加載力、擺角三者之間的關系，輸入多體動力學模型計算得到的力和擺角信號，就可以輸出得到應變-時間歷程，如圖9所示。

4.3 疲勞壽命計算

根據合適的疲勞損傷原則與實際工程中的疲勞損傷情況，可以得到疲勞失效標準并對橡膠元件進行疲勞壽命預測。盡管不少新的多軸疲勞損傷累積模型都具有很高的理論性，但工程上應用最廣泛的仍是Miner線性損傷累積模型，如式（11）所示：

式中，D為損傷值；c為臨界系數，暫取為1，即認為累積損傷達到1時失效；N1,N2,…Nl-1,Nl，為應變載荷εf1，εf2，…，εf(l-1)，εfl的疲勞壽命；n1，n2，n3，…，nl-1，nl為每個應變載荷的加載次數。

圖6 不同擺角下應變與加載力的關系曲線

圖7 不同加載力下應變與擺角的關系曲線

圖8 應變與加載力、擺角關系

應用雨流計數法和Miner線性損傷累積理論對應變時間歷程進行處理，就可以計算出橡膠襯套的疲勞壽命。仿真的應變最大位置如圖10所示。

4.4 橡膠襯套的疲勞試驗驗證

橡膠襯套的疲勞試驗在MTS的二通道疲勞試驗臺上進行，臺架關鍵部位如圖11所示。兩個加載通道分別是力輸入以及位移輸入，輸入的載荷是虛擬采譜法得到的目標信號。試驗開始前及過程中，需要測量空心側的剛度曲線，并用紅外測溫儀測量橡膠襯套的溫度。當零件橡膠本體裂紋長度達到一定尺寸時停止試驗，并記錄相對應的試驗次數。

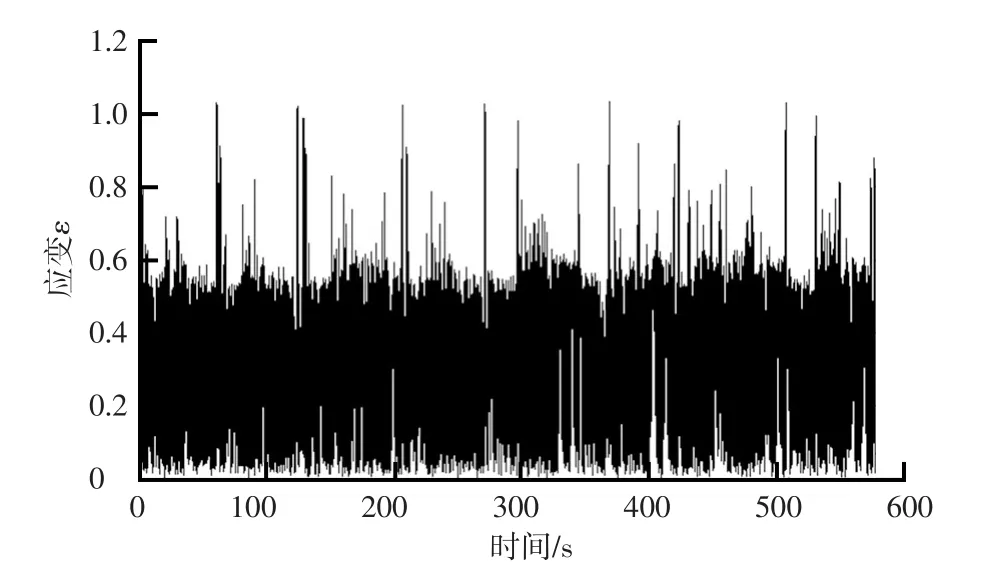
圖9 應變-時間歷程

圖10 仿真的應變最大位置

圖11 臺架關鍵部位示意

共進行了19個橡膠襯套的疲勞試驗，試驗的失效位置與仿真的位置是一致的（圖10），失效模式都是橡膠本體在交變載荷下的受拉失效。經計算，疲勞仿真的壽命與試驗的誤差僅為13.4%，預測壽命與實測壽命的比值僅為1.13倍，誤差較小，證明該預測方法的有效性。試驗與仿真壽命的對比結果如圖12所示，圖12中A～4A表示循環次數。由圖12可看出，實測壽命普遍低于預測壽命，這是由于仿真過程比較理想，而實際試驗過程中有許多不可控的因素，試驗條件比仿真的更惡劣。如,試驗過程中溫度的升高會對襯套的壽命有影響；其次，由于橡膠的裂紋長度很難第一時間測出，因此，橡膠襯套實際的壽命應該更低一些。綜上所述，該研究方法可行，仿真結果與實際試驗結果有較好的對應性，與以往的正弦輸入研究相比，此次的實際道路模擬工況輸入研究具有較高的參考價值。

圖12 仿真與試驗的壽命對比結果

5 結束語

本文通過臺架試驗與有限元仿真相結合的方法，準確地擬合了橡膠襯套各方向上的剛度特性，并對其在實際道路隨機振動工況下的壽命進行了預測。與以往傳統研究中的簡單工況相比，預測結果精度較高，與試驗結果更吻合，對實際設計研究有一定的參考意義，可以在橡膠襯套的設計初期預測其疲勞壽命，大大縮減開發周期。

1 Li Q,Zhao J C,Zhao B.Fatigue life prediction of a rubber mount based on test of material properties and finite ele?ment analysis.Engineering Failure Analysis,2009,16（7）: 2304～2310.

2 黃鵬程,王聰昌,陳凱.車用橡膠襯套疲勞的有限元分析.橡膠工業,2013,60（8）:488～492.

3 王文濤,上官文斌,段小成,等.基于線性疲勞累計損傷橡膠懸置疲勞壽命預測研究.機械工程學報,2012,48(10): 56～65.

4 Mars W V,Fatemi A.A literature survey on fatigue analysis approaches for rubber.International Journal of Fatigue, 2002,24（9）:949～961.

5 上官文斌,劉泰凱,王小莉,等.汽車動力總成橡膠懸置的疲勞壽命實測與預測方法.機械工程學報,2014,50（12）: 126～132.

6 王國權,劉萌,姚艷春,等.不同本構模型對橡膠制品有限元法適應性研究.力學與實踐,2013（4）:40～47.

（責任編輯 文 楫）

修改稿收到日期為2017年1月3日。

Fatigue Life Prediction of Rubber Bushing Based on Random Vibration

Wu Zhaojia1,Hou Yongping1,Zhang Jianwen2
（1.Clean Energy Automotive Engineering Center of Tongji University,Shanghai 201804;2.Shanghai Motor Vehicle Inspection Certification&Tech Innovation Center Co.,LTD,Shanghai 201805）

In this research,the model was established to predict the fatigue life of rubber material through test and finite element simulation,with the equivalent maximum principal strain as fatigue damage parameter.Van Der Waals constitutive equation was adopted to simulate the mechanical properties of rubber material,and the fatigue life was predicted under the road condition and random vibration with the accurate fitting rubber bushing stiffness characteristics.In comparison with the test,this method can accurately predict the fatigue life of the rubber bushing under multiaxial loading.

Rubber bush,Life prediction,Road test,Equivalent max principal strain

橡膠襯套 壽命預測 道路試驗 等效最大主應變

U467.4+97

A

1000-3703（2017）03-0024-05

國家自然科學基金項目（51275357）。