重型商用車鋼板彈簧懸架硬點優化設計

易晨陽張瑞亮陳澔利劉維達

（1.太原理工大學，太原 030024；2.大運汽車制造有限公司，運城 044000）

重型商用車鋼板彈簧懸架硬點優化設計

易晨陽1張瑞亮1陳澔利2劉維達1

（1.太原理工大學，太原 030024；2.大運汽車制造有限公司，運城 044000）

利用Adams/Car對某重型商用車鋼板彈簧前懸架進行建模及運動學特性仿真。針對仿真中出現的前束角和主銷后傾角變化過大的問題，結合鋼板彈簧結構特性進行分析，提出了懸架硬點設計變量的初選方案。采用靈敏度分析方法確定設計變量，通過響應面法對目標函數進行擬合，結合多目標遺傳優化算法NSGA-Ⅱ對懸架硬點坐標進行了優化。結果表明，前束角和主銷后傾角的變化分別減少了72.2%、68.2%，鋼板彈簧懸架運動學特性明顯的改善。

1 前言

鋼板彈簧懸架是目前商用車應用最為廣泛的懸架類型，其運動學特性與獨立懸架有較大的差別。懸架硬點布置決定了懸架運動學特性（Kinematics，簡稱K特性），即車輪定位參數在車輪跳動和轉向時的變化特性，它對車輛的操縱穩定性以及輪胎的磨損都有著直接的影響[1]。合理的硬點坐標對于改善懸架性能有著重要意義。文獻[2]采用牛頓迭代法對麥弗遜懸架的硬點坐標進行了優化；文獻[3]、文獻[4]分別采用目標規范法和多次迭代修改方法，以雙橫臂懸架的硬點坐標為設計變量，對懸架運動學特性進行了優化設計，改善了車輛的操縱穩定性；文獻[5]通過對雙橫臂扭桿式獨立懸架的硬點坐標進行優化匹配，改善了前束角和外傾角變化特性，減輕了輪胎磨損；文獻[6]、文獻[7]采用響應面法擬合目標函數，分別對雙橫臂懸架和多連桿懸架硬點進行了優化，相比其他方法，優化效率明顯提高。本文以某重型商用車鋼板彈簧前懸架為研究對象，利用Adams/Car建立其多體動力學模型，并分析了該懸架定位參數隨車輪跳動的變化情況，在文獻[7]的優化方法基礎上，結合鋼板彈簧懸架的運動學特性，采用了更高效的NSGA-Ⅱ遺傳算法，建立了從硬點初選、靈敏度分析、目標函數響應面法擬合到NSGA-Ⅱ多目標優化的完整優化設計流程，對懸架硬點坐標進行優化設計，改善了懸架性能。

2 鋼板彈簧前懸架模型的建立

鋼板彈簧前懸架模型由鋼板彈簧子系統、轉向機構子系統和轉向懸架子系統組成。鋼板彈簧前懸架的設計硬點名稱及坐標如表1所示。

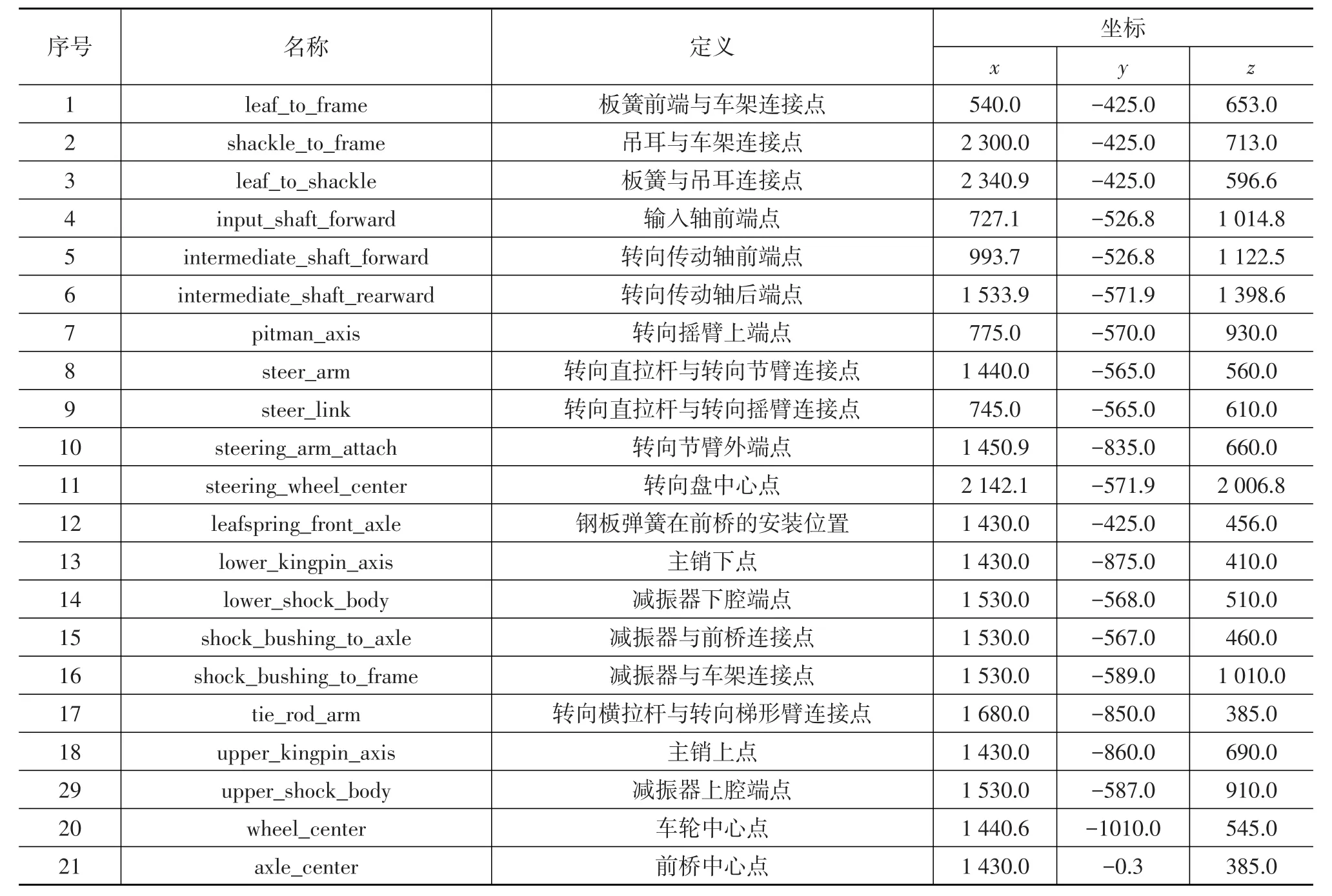
表1 鋼板彈簧前懸架設計硬點坐標 mm

2.1 鋼板彈簧子系統建模

鋼板彈簧不同于其他懸架彈性單元，其不但具有承載功能，還具有導向功能和一定的減振作用。鋼板彈簧的導向作用對于懸架運動學特性有著直接的影響。因此，應用于懸架運動學特性仿真的鋼板彈簧模型的簡化過程不能只考慮其剛度特性。本文采用離散梁方法[8]建模。鋼板彈簧子系統共3個設計硬點（對稱位置記左側坐標），其坐標值見表1中的第1點～第3點。

2.2 轉向機構子系統建模

利用Adams/Car建立的轉向機構子系統包括轉向盤、轉向管柱、轉向軸、轉向傳動軸、轉向器輸入軸、轉向器、轉向搖臂、轉向直拉桿和轉向節臂。轉向機構子系統共8個設計硬點，其坐標值見表1中的第4點～第11點。

2.3 轉向懸架子系統建模

按照Adams/Car中的子系統劃分方法，將前懸架中的轉向橋與減振器劃入轉向懸架子系統。根據目標車輛實際結構進行適當簡化，建立的轉向懸架子系統模型具體包括減振器、前橋、轉向梯形臂、轉向橫拉桿和轉向節。轉向懸架子系統共10個設計硬點，其坐標值見于表1中的第12點～第21點。

將上述3個子系統與Adams/Car中的懸架試驗臺進行裝配，并根據實車數據設置試驗臺相關參數（見表2），得到圖1所示的鋼板彈簧前懸架模型。

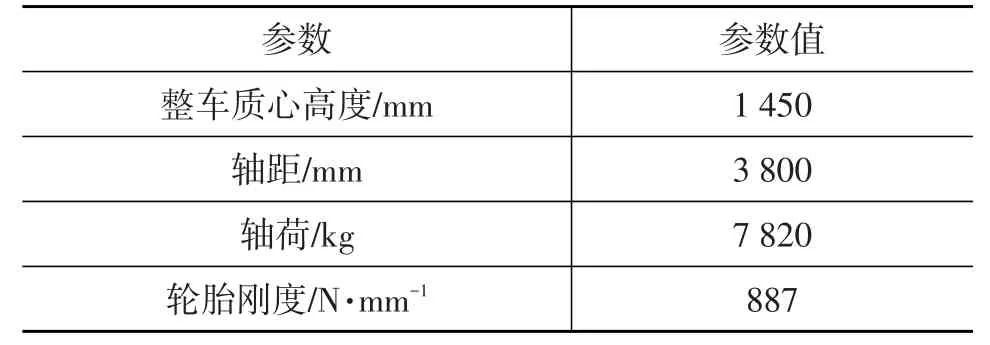
表2 懸架試驗臺參數

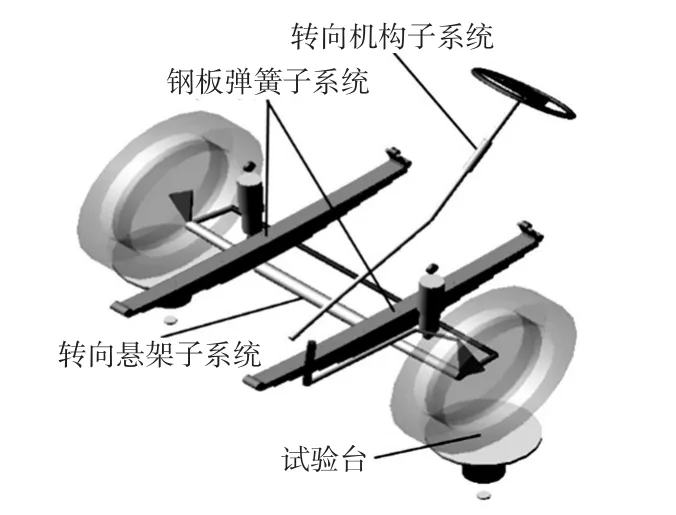
圖1 鋼板彈簧前懸架模型

3 懸架運動學特性仿真分析

商用車總質量一般較大，特別是重型商用車，軸荷普遍達到數噸。目前，國內現有的懸架K&C特性試驗臺主要用于軸荷較小的乘用車懸架特性測試，不能滿足重型商用車懸架特性的測試要求。因此，采用試驗方法獲得懸架運動學特性存在諸多困難。Adams軟件中可以建立精確的懸架模型，并通過專業的懸架測試模塊分析懸架的運動學特性，成為獲取重型商用車懸架運動學特性分析的有效途徑。

3.1 仿真設計

車輪平行跳動引起的前束角、車輪外傾角、主銷內傾角和主銷后傾角等4個定位參數的變化是分析懸架運動是否合理的重要依據，可以較為全面地反映懸架的運動學特性。平行輪跳仿真的主要參數設置為：車輪跳動高度范圍為-60～60 mm，仿真步數為100，仿真模式為運動學（Kinematic）模式。

3.2 懸架運動學特性分析

各定位參數設計值如表3所示，定位參數隨車輪跳動的變化曲線如圖2所示。

表3 車輪定位參數設計值 （°）

圖2 定位參數與車輪跳動量的關系

由仿真結果可以看出，車輪外傾角和主銷內傾角隨車輪跳動的變化較小，滿足設計要求。前束角和主銷后傾角隨車輪跳動的變化較大，會導致車輛行駛穩定性惡化、輪胎磨損異常，因此需要進一步優化。

3.3 懸架硬點的初選

根據前束角、車輪外傾角、主銷內傾角和主銷后傾角等4個定位參數隨車輪跳動的變化特性，結合鋼板彈簧懸架的結構特性和使用工況，對定位參數變化的原因及與其相關的懸架硬點進行分析，并進行懸架硬點的初選。

前束角隨車輪跳動而產生變化的主要原因是懸架系統導向機構與轉向系統的垂直運動和橫擺運動的互相干涉。本文所建立的鋼板彈簧懸架模型中未加裝其他導向桿系，因此主要由鋼板彈簧起導向作用。鋼板彈簧的剛度特性、幾何特性以及安裝位置都對其導向性能有直接的影響。在盡量不影響懸架承載性能的前提下，考慮選擇鋼板彈簧安裝位置硬點坐標在合理的范圍內進行優化，是減小前束角變化較為合理的途徑。因此，選出鋼板彈簧前端與車架連接位置、吊耳與車架連接位置、鋼板彈簧后端與吊耳連接位置和鋼板彈簧在前橋上安裝位置共4個硬點（硬點序號分別為1、2、3和11）。轉向系統考慮有空間運動而非繞自身軸線旋轉的桿件，同時不能影響各定位參數初始值，初步確定轉向節臂與轉向直拉桿連接位置和轉向橫拉桿與轉向梯形臂連接位置共2個硬點（硬點序號分別為8和17）。

主銷后傾角隨車輪跳動而產生變化的主要原因是懸架系統導向機構與轉向系統的垂直運動和俯仰運動的互相干涉。考慮到鋼板彈簧懸架的主銷真實存在且與剛性前橋固定，兩者在主銷后傾角變化方向上沒有相對運動。由此推斷是由于鋼板彈簧在車輪跳動時的不正常運動特性和變形特性導致前橋出現俯仰運動，帶動主銷運動，使得主銷后傾角發生變化。因此，鋼板彈簧安裝位置硬點坐標也是主銷后傾角變化的主要原因。

主銷內傾角隨車輪跳動幾乎不發生變化是由于主銷與剛性車橋固定，車橋不存在彎曲變形，使得主銷內傾角可以得到較好的保持。在不改變前橋與主銷相關硬點的情況下，其他硬點的變動對主銷內傾角影響非常小。

由于鋼板彈簧懸架是非獨立懸架，車輪通過車橋剛性連接，在不考慮車橋彎曲變形的情況下，車輪外傾角的變化主要是主銷后傾角和前束角共同作用導致的，當主銷后傾角不為0°時，前束角的變化（相當于車輪轉向運動）會導致車輪外傾角的變化[9]，在主銷后傾角較小的情況下，這種變化也相當有限。

綜合上述分析結論，初步選出共6個相關硬點，分別為表1中序號為1、2、3、8、11和17的硬點。

4 懸架硬點優化設計

4.1 靈敏度分析

通過進行靈敏度分析，可以得出各設計因素對目標函數的影響大小，進而選擇出合理的因素進行優化設計，提高優化工作的效率。

以平行輪跳仿真為基礎，前束角和主銷后傾角隨車輪跳動變化量大小為響應函數，對初選的6個相關懸架硬點x、y、z向坐標參數共18個變量進行靈敏度分析。各硬點坐標的擾動范圍設置為-10～10 mm。通過正交試驗法進行了2水平篩選法仿真，共進行48次仿真。最終得出了各硬點坐標對前束角和主銷后傾角隨車輪跳動的變化量的影響大小，如表4所示。

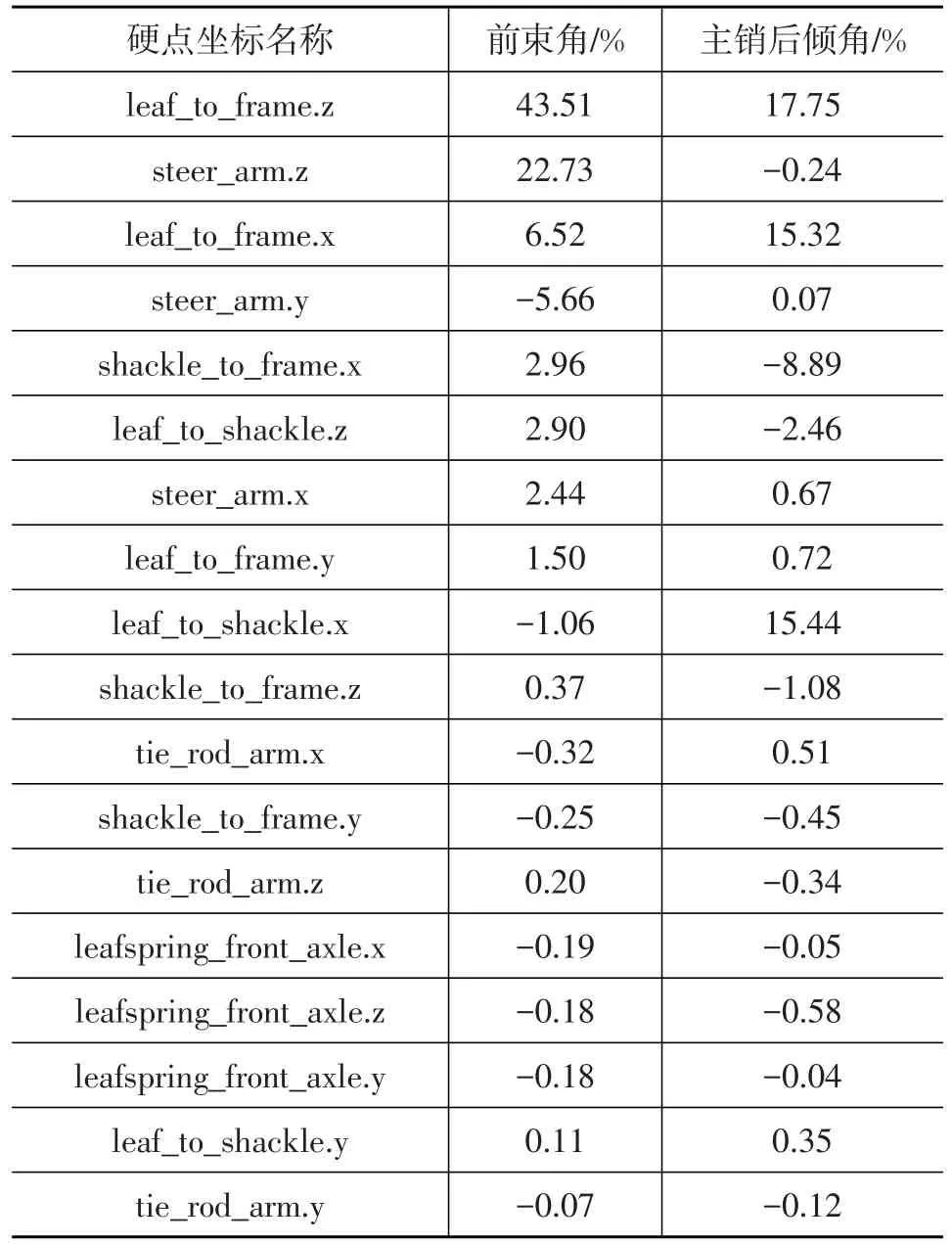
表4 靈敏度分析結果

為了提高前束角和主銷后傾角的優化效率，根據靈敏度分析結果，將對前束角或主銷后傾角的影響大于10%的變量選出。由表4可知：硬點坐標leaf_to_frame.z和 steer_arm.z對前束角的影響較大；硬點坐標leaf_to_frame.z、leaf_to_shackle.x和leaf_to_frame.x對主銷后傾角的影響較大。因此考慮選取上述4個硬點的坐標作為優化變量，分別記為x1、x2、x3、x4。

4.2 目標函數的響應面法擬合

根據靈敏度分析的結果，選取上述4個優化變量，利用Adams/Insight分別對前束角和主銷后傾角2個目標函數進行擬合。仿真策略采用響應面法（DOE Response Surface），選擇二次模型進行擬合，采用拉丁超立方（Latin Hypercube）設計方法，共進行100次仿真。

前束角擬合函數結果為：

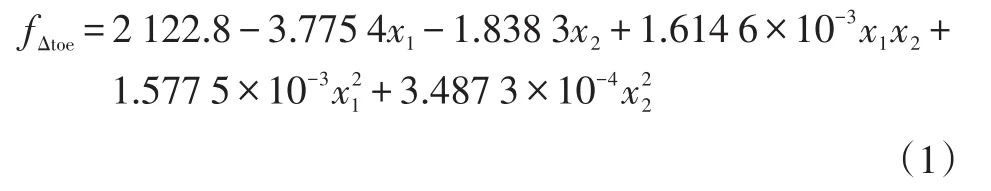
主銷后傾角擬合函數結果為：

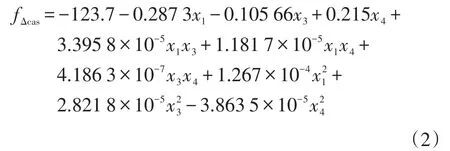
通過擬合優度（Goodness-of-fit）檢查擬合效果，2次擬合的各項指標值如表5所示。其中，可決系數R2越接近1，說明擬合優度越高，對于較好的擬合，R2通常大于0.9；修正可決系數R2adj越接近1也說明擬合效果越好；P值反映擬合項的顯著性，它越小說明擬合效果越好，一般要求P值小于0.02；R/V為模型的計算值與原始數據點之間的關系，該值越大說明擬合結果可信度越高，一般要求R/V大于10。從表5可以看出，擬合效果比較理想。

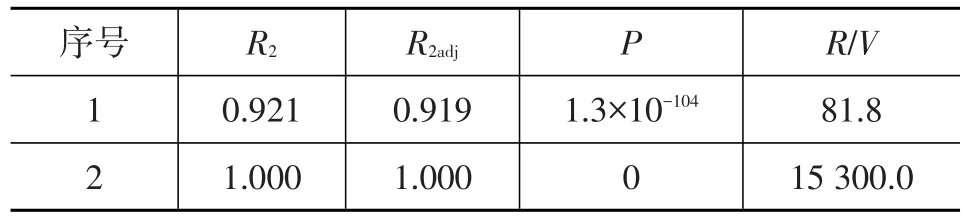
表5 擬合優度指標結果

4.3 基于NSGA-Ⅱ算法的多目標優化

帶精英策略的快速非支配排序遺傳算法（NSGA-Ⅱ）是目前應用最廣泛也是最優秀的多目標優化算法之一，其具有運行速度快、收斂性好、Pareto最優解集分布均勻等特點。

根據目標函數的響應面法擬合結果，建立多目標優化模型為：

式中，xio為xi的原始值。

設置種群大小為200，最優前端個體系數為0.2，交叉概率為0.8，變異概率為0.1，進化代數為500。經過計算得到Pareto最優解集如圖3所示。

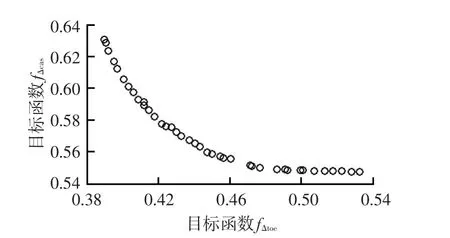
圖3 Pareto最優解集分布

由圖3可知，目標函數fΔtoe和fΔcas之間存在沖突，從綜合性能的角度考慮，選取中間段的Pareto最優解較為合適。考慮到對變量參數的改動應盡量小，從而不影響懸架的其他性能，在中間段幾個相近解中選擇本次優化的最終解，其對應的優化變量取值對比如表6所示。

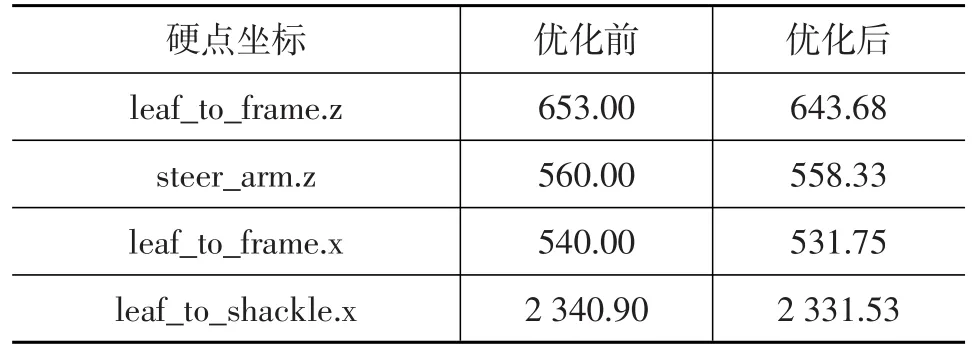
表6 懸架硬點坐標優化結果 mm

按照優化后的硬點坐標對原鋼板彈簧前懸架模型進行修改，對優化后的懸架在相同工況下進行仿真。優化前、后車輪定位參數隨車輪跳動的變化曲線對比如圖4所示。

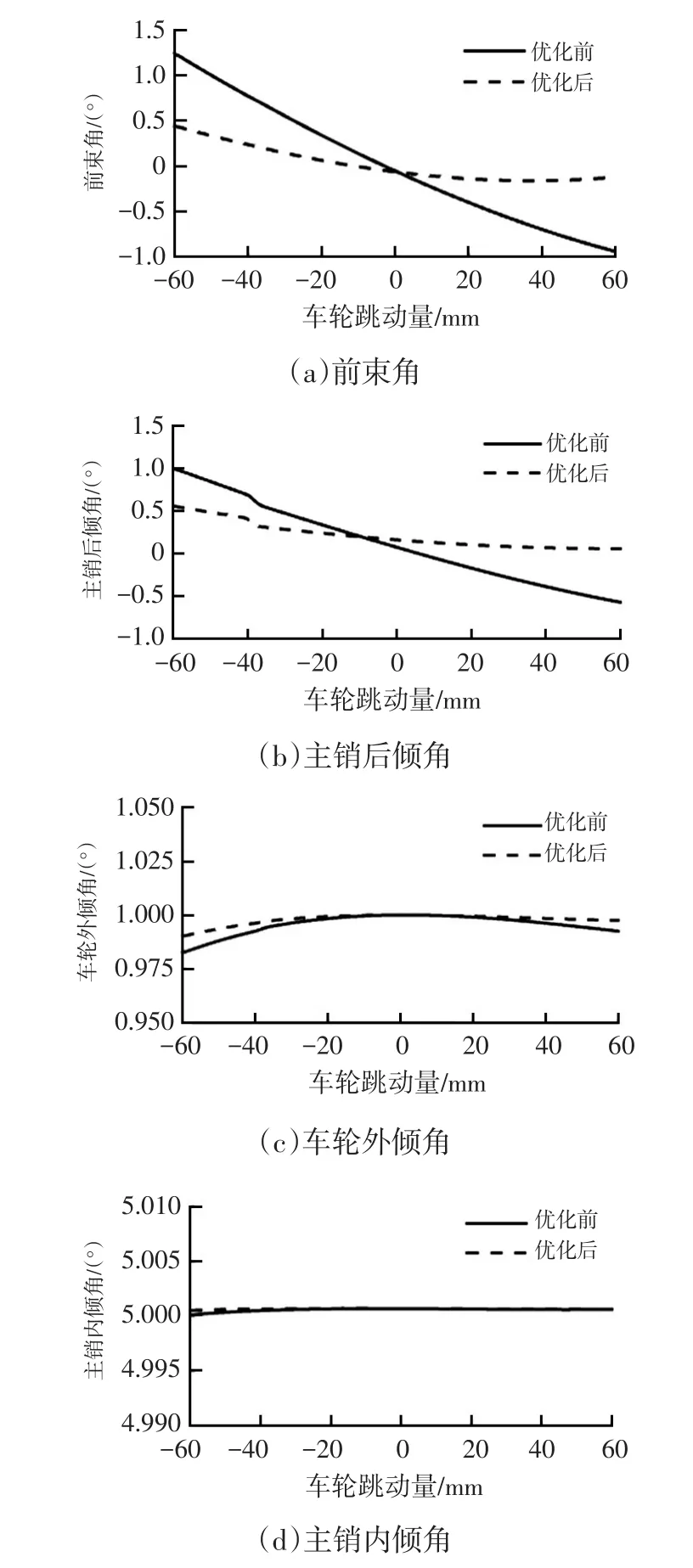
圖4 優化前、后定位參數與車輪跳動量的關系

5 結論

通過Adams/Car建立了某商用車鋼板彈簧前懸架多體動力學模型。通過平行輪跳仿真對其懸架運動學特性進行了仿真，并根據仿真結果，結合鋼板彈簧懸架的結構特性，對定位參數變化的原因及與其相關的懸架硬點進行分析，為懸架硬點的初選提供了指導。

通過Adams/Insight對初選的硬點坐標進行靈敏度分析，確定了影響最大的4個硬點坐標為最終的優化變量。運用響應面法對目標函數進行擬合，并檢驗了擬合優度，確定了多目標優化模型。基于該模型，通過NSGA-Ⅱ算法進行了多目標優化，得到了前束角和主銷后傾角變化的兩目標Pareto最優解集。該方法提高了多目標優化的效率，并為工程設計人員提供了靈活的設計空間選擇。

最后，選擇出最優解驗證了優化效果。通過對鋼板彈簧懸架硬點的優化，懸架運動學特性顯著改善，對于改善車輛操縱穩定性、減小輪胎磨損有重要意義。

1 石琴.前懸架K&C特性優化設計及整車操縱穩定性分析.合肥：合肥工業大學，2012.

2 廖永升，劉擁軍，陳璟，等.基于ADAMS的麥弗遜懸架運動學優化.科學技術與工程，2012（20）：4935～4940+4950.

3 丁亞康，翟潤國，井緒文.基于ADAMS/INSIGHT的汽車懸架定位參數優化設計.汽車技術，2011（5）：33～36.

4 向鐵明，沈理真.基于ADAMS的某賽車前懸架桿系優化.汽車工程，2014（4）：486～490.

5 馮金芝，梁鵬，鄭松林，等.扭力梁后懸架K&C特性仿真分析.現代制造工程，2015（10）：57～61.

6 唐應時，朱位宇，朱彪，等.基于輪胎磨損的懸架與轉向系統硬點優化.汽車工程，2013（7）：640～644+653.

7 Topa? M M,Deryal U,Bahar E,et al.Optimal kinematic design of a multi-link steering system for a bus independent suspension: An application of response surface methodology.Mechanika，2015，21（5）：404～413.

8 李杰，朱毅杰，劉煜.鋼板彈簧建模模塊LeafSpring的研究及其應用.科學技術與工程，2011（30）：7555～7559+7569.

9 王霄鋒.汽車懸架和轉向系統設計.北京：清華大學出版社，2015.

（責任編輯 斛 畔）

修改稿收到日期為2016年11月9日。

Optimal Design of Leaf-Spring Suspension Hard-points for a Heavy Commercial Vehicle

Yi Chenyang1,Zhang Ruiliang1,Chen Haoli2,Liu Weida1
（1.Taiyuan University of Technology,Taiyuan 030024;2.Shanxi Dayun Automobile Manufacturing Co.,Ltd., Yuncheng 044000）

Modeling and kinematic properties simulation of leaf-spring front suspension for a heavy commercial vehicle was made with software Adams/Car.The simulation showed oversized changes of the toe angle and caster angle.To solve this problem,we analyzed leaf-spring structural characteristics,and proposed a primary program which set the suspension hard points as design variables.The design variables were determined by the method of sensitivity analysis,and the objective functions were fitted by response surface method,the suspension hard point coordinates were optimized by multi-objective genetic algorithm NSGA-Ⅱ method.The results showed that,the changes of toe angle and caster angle were reduced by 72.2%and 68.2%respectively,the leaf-spring suspension kinematic properties were improved dramatically.

Leaf-spring suspension,K&C characteristic,Hard-points coordinate,NSGA-II multi-objective optimization

鋼板彈簧懸架 K&C特性 硬點坐標 NSGA-Ⅱ多目標優化

U467.1

A

1000-3703（2017）03-0033-05