因“圍”精彩
——《釘子板上圍圖形》教學片斷實錄與點評

李 量 邢佳立

“玩”是兒童的天性，兒童的智慧有時候就是在指尖上玩出來的。但現實中，作為數學教師，卻常常因為“教學任務”“課業壓力”無奈地讓學生沉浸于“題海”之中。是不是可以有一種“玩”，能夠讓學生沉浸其中，同時為課堂內的“學”奠定基礎，讓學生因今天的“玩”而更好地促進明天的“學”，讓學生不但玩得快樂，更玩得出彩？

筆者在新思維教科院指導下嘗試的數學實驗課《釘子板上圍圖形》，就是這樣一節課，現與大家分享。

【片斷實錄1】

（教師舉起一塊釘子板）

師：這塊塑料板上有很多凸起的塑料釘，它叫釘子板。在釘子板上可以用橡皮筋圍出很多圖形，怎么圍呢？

（教師舉起一塊有圍好圖形的釘子板，停頓兩秒后快速放下）

師：釘子板上圍了一個什么圖形？占幾格？

生：是一個長方形，占6格。

師：你只看了一眼，怎么就知道了？

生：我看到它有2排，每排3個格子，所以是6格。

（教師再次舉起釘子板，引導學生一起數出6格）

【點評：“占幾格”是學生生活化的語言，雖然學生還沒有面積的概念，但有數“格子”的生活經驗，這里的“圍”強調的內核即“封閉圖形”，占幾格其實就是“圖形的面積”。老師快速舉起再放下釘子板，不但起到了調動學習興趣、快速集中學生注意力的作用，同時也“逼”著學生想出“有2排，每排3格，一共6格”這樣的“數”法，為后繼長方形面積的教學積累了直觀的活動經驗。】

（教師舉起第二塊釘子板并快速放下）

師：看到了什么圖形？占幾格？

生：是一個正方形，占4格。

（教師舉起第三塊釘子板并快速放下）

生：我覺得是一個鉆石形，占3格半。

師：這個形狀看起來的確有點像鉆石。不過在數學的世界里，像這樣不怎么規則的圖形，我們一般都是按照它邊的多少來稱呼它的。比如說這個圖形有5條邊，我們就叫它——五邊形。

師：再來個難一點的！（一邊說一邊舉起放下第4塊釘子板）什么圖形？占幾格？

生：是一個平行四邊形，占2格。

師：占兩格你是怎么數的？

生：半格加半格就是1格，1格和1格合起來就是2格。

【點評：在這一小段教學中，“多邊形”“一格的一半是半格”“面積的可加性（半格+1格+半格=2格）”“面積的等積變換（把這半格放在這兒，就是1格）”等內容都在師生對話與交流中自然而然的滲透出來。】

【片斷實錄2】

師：這個平行四邊形占2格，在釘子板上還能圍出占2格的圖形嗎？想想看，你能圍出幾種？

師：把你想到的在練習紙上畫一畫。畫好以后再在釘子板上圍一圍，如果圍出了你沒想到的圖形，也把它畫下來。

（學生獨立活動7分鐘）

交流反饋：

（1）首先介紹多數學生找到的長方形、直角三角形、梯形。在反饋中引導學生思考“是占兩格嗎？為什么？”

（學生作品略）

（2）哪位同學覺得你畫出了比較特別的，但同樣占2格的圖形？

生：我這個斜著看像個狐貍的頭，也是占兩格！

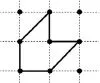
師：它是占兩格嗎？你怎么想到的？

生：我先畫1個格子，在這里加半格，在這里再加半格，就是這樣了！

師：我們都是圍出來以后再數是不是2格，這位同學能倒回去想，只要是一個1格再加上兩個半格，一定是占兩格的圖形！

師：在他的啟發下，你還能想出其他圖形嗎？

生：我還有不一樣的。

師：這個圖形也占2格嗎？我找不到1格，也找不到半格啊！

生：我是這樣想的，把這兒拿掉，拼到這兒，就是一個占2格的長方形。

師：剛才我們想到更多的是加一加，把半格、1格加起來，湊成2格，這樣的方法咱們可以稱它為“累加”；現在想到的是這邊拿掉，就像剪刀剪下來一樣，拼到另一邊，這個方法就叫它“剪拼”可以吧！都能得到兩格。還有嗎？

生：我這個看起來不太像2格，但它也是占2格。

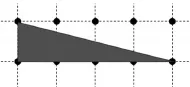
師：你說它是2格，有什么理由嗎？

生：兩個一樣的這種圖形拼在一起占4格，所以一個這種圖形占2格。

生：這樣圍起來是4個格子，這邊剛剛好是一半，就是2格了！

【點評：在這一環節中，學生經歷了猜——圍——畫——說的過程。猜：不是沒有根據的胡思亂想，而是對解決眼前問題的可能性的一種想象。圍：有目的地圍，通過外在的、直觀的行為，將內在的對圖形面積的思考表征出來，并作驗證和調整。畫：落實想法。說：反思與交流，進一步加深對概念、規則的理解，不但知其然，更知其所以然。

“圍”出占2格的圖形，學生（也包括我們教師）容易想到的往往都是規則圖形——長方形、平行四邊形、梯形，但一個“先圍1格，再加上2個半格”的想法，圍出了不規則的圖形，打破了學生認知的局限，學生的思路一下子被打開了！接著“這邊拿下來拼到那邊”，等積割補的方法自然而然地產生，更精彩的是“取一半”！有經驗的教師都知道，要讓學生主動想到將“兩個同樣的三角形拼起來”很不容易，而這一環節中“取一半”是學生在“圍”、“觀察”和“思考”中自然感悟到的——這就是在積累豐富的直觀經驗，我們相信，這些經驗是幾何思維的“活水”，在高年級學習基本圖形和組合圖形面積時，一定會發揮出它的作用。】

【片斷實錄3】

師：如果圍占3格的圖形，你能圍幾個？

生：10個！20個！

生：肯定比圍占2格的還多得多！

（學生獨立操作7分鐘后交流）

師：好多同學已經畫了十幾二十個，我還看到一個同學已經畫滿了，他怎么想到這么多的呢？

（請出畫的特別多的學生）

生：我前面這些就是在2格的基礎上再加上1個格子，而且這1個格子可以加在不同的位置，還可以先加半格再加半格，這樣一個就變成了好幾個！最后面這幾個我是想，4格的一半是2格，6格的一半就是3格，我就先畫6格的長方形、梯形、平行四邊形，然后取它們的一半。

【點評：學習重在遷移！“4格的一半是2格，6格的一半就是3格”，學生的遷移自然而然地發生。同樣“在2格基礎上加上1個格子，或者加2個半格就是3個格子了！”體現了學生能夠充分利用現有的資源——2格，解決新問題——3格，化歸思想在這里體現，樸素而又深刻！】